Discussion of Leecode question

LRU

We will used the doubly-linked list to build the LRU Dlink will have the prev pointer and the next pointer

the key :when we put new element into LRU we need to check whether we should remove the less used element, the key is used to use the method map.remove(redn.key) and update the hashmap

the value: use it to store the value;

the map : used to find the Dlinknode to choose update or delete the Dlinknode;

important method: addtohead removenode

class DLinkedNode {
        int key;
        int value;
        DLinkedNode prev;
        DLinkedNode next;
        public DLinkedNode() {}
        public DLinkedNode(int _key, int _value) {key = _key; value = _value;}
    }
    Map<Integer,DLinkedNode> map=new HashMap<>();
    private int size;
    private int capacity;
    private DLinkedNode head, tail;
        public  LRUCache(int capacity) {
            this.capacity=capacity;
            this.size=0;   
            head=new DLinkedNode();
            tail=new DLinkedNode();
            head.next=tail;
            tail.prev=head;
        }

        public int get(int key) {
            DLinkedNode dn = map.get(key);
            if (dn == null) {
                return -1;
            }
            moveToHead(dn);
            return dn.value;
        }

        public void put(int key, int value) {
            DLinkedNode dn=map.get(key);
            if(dn==null){
                DLinkedNode node=new DLinkedNode(key,value);
                addToHead(node);
                map.put(key, node);
                size++;
                if(size>capacity) {
                    DLinkedNode redn = removeTail();
                    map.remove(redn.key);
                    size--;
                }
            }
             else {
                dn.value=value;
                moveToHead(dn);
            }

        }

    private void addToHead(DLinkedNode node) {
        node.prev = head;
        node.next = head.next;
        head.next.prev = node;
        head.next = node;
    }

    private void removeNode(DLinkedNode node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }

    private void moveToHead(DLinkedNode node) {
        removeNode(node);
        addToHead(node);
    }

    private DLinkedNode removeTail() {
        DLinkedNode res = tail.prev;
        removeNode(res);
        return res;
    }

With the time expiring requirement

import java.util.HashMap;
import java.util.Map;

// 定义双向链表节点
class Node<K, V> {
    K key;
    V value;
    long expireTime;
    Node<K, V> prev;
    Node<K, V> next;
    
    public Node(K key, V value, long expireTime) {
        this.key = key;
        this.value = value;
        this.expireTime = expireTime;
    }
}

// 实现带过期时间的LRU缓存
public class LRUCacheWithExpiration<K, V> {
    private final int capacity;
    private final Map<K, Node<K, V>> cache;
    private final Node<K, V> head; // 最近访问的节点（头部）
    private final Node<K, V> tail; // 最久未访问的节点（尾部）

    public LRUCacheWithExpiration(int capacity) {
        this.capacity = capacity;
        this.cache = new HashMap<>();
        this.head = new Node<>(null, null, 0);
        this.tail = new Node<>(null, null, 0);
        this.head.next = this.tail;
        this.tail.prev = this.head;
    }

    public V get(K key) {
        Node<K, V> node = cache.get(key);
        if (node != null) {
            // 检查是否过期
            if (node.expireTime < System.currentTimeMillis()) {
                removeNode(node);
                cache.remove(key);
                return null;
            }
            // 移动节点到头部（表示最近使用）
            moveToHead(node);
            return node.value;
        }
        return null;
    }

    public void put(K key, V value, long expireTimeMillis) {
        // 如果 key 已存在，则更新 value 和过期时间
        if (cache.containsKey(key)) {
            Node<K, V> node = cache.get(key);
            node.value = value;
            node.expireTime = System.currentTimeMillis() + expireTimeMillis;
            moveToHead(node);
        } else {
            // 新节点插入到头部
            Node<K, V> newNode = new Node<>(key, value, System.currentTimeMillis() + expireTimeMillis);
            cache.put(key, newNode);
            addToHead(newNode);
            
            // 如果超过容量，删除尾部节点
            if (cache.size() > capacity) {
                Node<K, V> tailNode = removeTail();
                cache.remove(tailNode.key);
            }
        }
    }

    private void addToHead(Node<K, V> node) {
        node.prev = head;
        node.next = head.next;
        head.next.prev = node;
        head.next = node;
    }

    private void removeNode(Node<K, V> node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }

    private Node<K, V> removeTail() {
        Node<K, V> tailNode = tail.prev;
        removeNode(tailNode);
        return tailNode;
    }

    private void moveToHead(Node<K, V> node) {
        removeNode(node);
        addToHead(node);
    }
}



public void put(K key, V value, long expireTimeMillis) {
    // 如果 key 已存在，则更新 value 和过期时间
    if (cache.containsKey(key)) {
        Node<K, V> node = cache.get(key);
        node.value = value;
        node.expireTime = System.currentTimeMillis() + expireTimeMillis;
        moveToHead(node);
    } else {
        // 新节点插入到头部
        Node<K, V> newNode = new Node<>(key, value, System.currentTimeMillis() + expireTimeMillis);
        cache.put(key, newNode);
        addToHead(newNode);
        
        // 如果超过容量，删除尾部节点
        if (cache.size() > capacity) {
            removeExpiredNodes();
            if (cache.size() > capacity) {
                Node<K, V> tailNode = removeTail();
                cache.remove(tailNode.key);
            }
        }
    }
}

private void removeExpiredNodes() {
    Node<K, V> node = tail.prev;
    while (node != head && node.expireTime < System.currentTimeMillis()) {
        removeNode(node);
        cache.remove(node.key);
        node = tail.prev;
    }
}

Kruskal

//1584. Min Cost to Connect All Points  https://leetcode.com/problems/min-cost-to-connect-all-points/
    public int minCostConnectPoints(int[][] points) {
        int n = points.length;
        DisjointSetUnion dsu = new DisjointSetUnion(n);
        List<Edge> edges = new ArrayList<Edge>();
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                edges.add(new Edge(dist(points, i, j), i, j));
            }
        }
        Collections.sort(edges, new Comparator<Edge>() {
            public int compare(Edge edge1, Edge edge2) {
                return edge1.len - edge2.len;
            }
        });
        int ret = 0, num = 1;
        for (Edge edge : edges) {
            int len = edge.len, x = edge.x, y = edge.y;
            if (dsu.unionSet(x, y)) {
                ret += len;
                num++;
                if (num == n) {
                    break;
                }
            }
        }
        return ret;
    }
    public int dist(int[][] points, int x, int y) {
        return Math.abs(points[x][0] - points[y][0]) + Math.abs(points[x][1] - points[y][1]);
    }

    class DisjointSetUnion {
        int[] f;
        int[] rank;
        int n;

        public DisjointSetUnion(int n) {
            this.n = n;
            this.rank = new int[n];
            Arrays.fill(this.rank, 1);
            this.f = new int[n];
            for (int i = 0; i < n; i++) {
                this.f[i] = i;
            }
        }

        public int find(int x) {
            return f[x] == x ? x : (f[x] = find(f[x]));
        }

        public boolean unionSet(int x, int y) {
            int fx = find(x), fy = find(y);
            if (fx == fy) {
                return false;
            }
            if (rank[fx] < rank[fy]) {
                int temp = fx;
                fx = fy;
                fy = temp;
            }
            rank[fx] += rank[fy];
            f[fy] = fx;
            return true;
        }
    }
    class Edge {
        int len, x, y;

        public Edge(int len, int x, int y) {
            this.len = len;
            this.x = x;
            this.y = y;
        }
    }

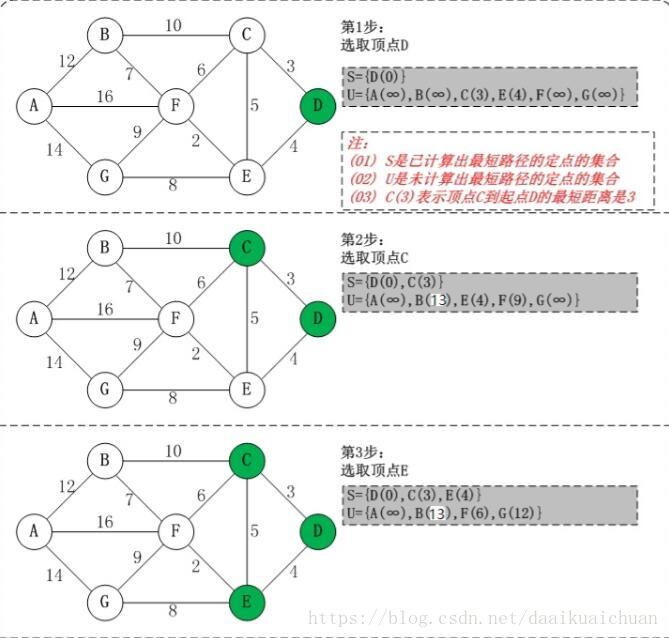
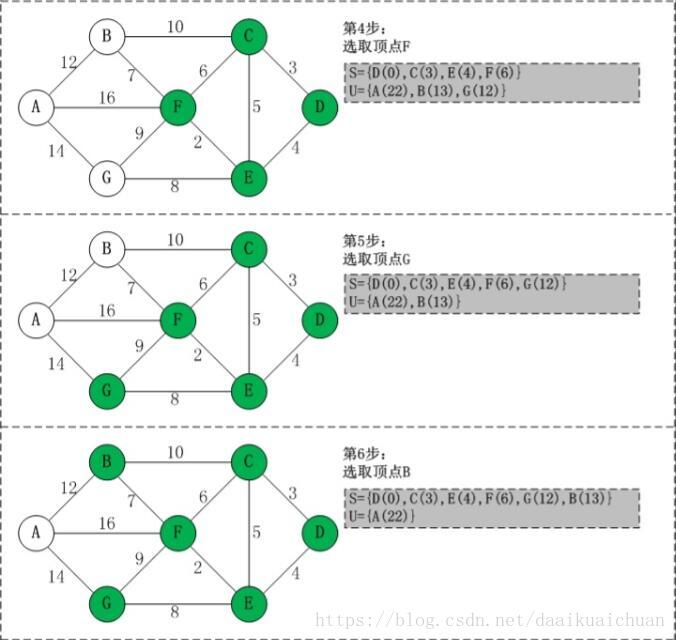
Dijkstra

//743. Network Delay Time  https://leetcode.com/problems/network-delay-time/
    public int networkDelayTime(int[][] times, int n, int k) {
        final int INF = Integer.MAX_VALUE / 2;
        int[][] g = new int[n][n];
        for (int i = 0; i < n; ++i) {
            Arrays.fill(g[i], INF);
        }
        for (int[] t : times) {
            int x = t[0] - 1, y = t[1] - 1;
            g[x][y] = t[2];
        }
        int[] dist = new int[n];
        Arrays.fill(dist, INF);
        dist[k - 1] = 0;
        boolean[] used = new boolean[n];
        for (int i = 0; i < n; i++) {
            int x=-1;
            for (int y = 0; y < n; y++) {
                if(!used[y]&&(x==-1||dist[y]<dist[x])){
                    x=y;
                }
            }
            used[x]=true;
            for (int y = 0; y < n; y++) {
                 dist[y]=Math.min(dist[y],dist[x]+g[x][y]);
            }
        }
        int ans = Arrays.stream(dist).max().getAsInt();
        return ans == INF ? -1 : ans;
    }

1976. 到达目的地的方案数

public int countPaths(int n, int[][] roads) {
    int mod = 1000000007;
    List<int[]>[] e = new List[n];
    for (int i = 0; i < n; i++) {
        e[i] = new ArrayList<int[]>();
    }
    for (int[] road : roads) {
        int x = road[0], y = road[1], t = road[2];
        e[x].add(new int[]{y, t});
        e[y].add(new int[]{x, t});
    }
    long[] dis = new long[n];
    Arrays.fill(dis, Long.MAX_VALUE);
    int[] ways = new int[n];

    PriorityQueue<long[]> pq = new PriorityQueue<long[]>((a, b) -> Long.compare(a[0], b[0]));
    pq.offer(new long[]{0, 0});
    dis[0] = 0;
    ways[0] = 1;

    while (!pq.isEmpty()) {
        long[] arr = pq.poll();
        long t = arr[0];
        int u = (int) arr[1];
        if (t > dis[u]) {
            continue;
        }
        for (int[] next : e[u]) {
            int v = next[0], w = next[1];
            if (t + w < dis[v]) {
                dis[v] = t + w;
                ways[v] = ways[u];
                pq.offer(new long[]{t + w, v});
            } else if (t + w == dis[v]) {
                ways[v] = (ways[u] + ways[v]) % mod;
            }
        }
    }
    return ways[n - 1];
}

Floyd

画每个节点的距离表格

class Solution {
    int N = 110, M = 6010;
    // 邻接矩阵数组：w[a][b] = c 代表从 a 到 b 有权重为 c 的边
    int[][] w = new int[N][N];
    int INF = 0x3f3f3f3f;
    int n, k;
    public int networkDelayTime(int[][] ts, int _n, int _k) {
        n = _n; k = _k;
        // 初始化邻接矩阵
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                w[i][j] = w[j][i] = i == j ? 0 : INF;
            }
        }
        // 存图
        for (int[] t : ts) {
            int u = t[0], v = t[1], c = t[2];
            w[u][v] = c;
        }
        // 最短路
        floyd();
        // 遍历答案
        int ans = 0;
        for (int i = 1; i <= n; i++) {
            ans = Math.max(ans, w[k][i]);
        }
        return ans >= INF / 2 ? -1 : ans;
    }
    void floyd() {
        // floyd 基本流程为三层循环：
        // 枚举中转点 - 枚举起点 - 枚举终点 - 松弛操作        
        for (int p = 1; p <= n; p++) {
            for (int i = 1; i <= n; i++) {
                for (int j = 1; j <= n; j++) {
                    w[i][j] = Math.min(w[i][j], w[i][p] + w[p][j]);
                }
            }
        }
    }
}

BellmanFord

Dijstra不能运用在含负权边的图

利用Dijstra算法，可以得到最短路径为：1 -> 2 -> 4 -> 5，因此算出最短路径为2+2+1 = 5。然而还存在一条路径即1 -> 3 -> 4 -> 5，他的最短路径长度为5+(-2)+1=4，因此Dijstra算法失效。

for n 次：
  for 所有边 a , b , w （松弛操作）
    dist[b] = min(dist[b], backup[a] + c)

下面有一个有边数限制的最短路问题：

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你求出从 1 号点到 n 号点的最多经过 k 条边的最短距离，如果无法从 1 号点走到 n 号点，输出 impossible。

import java.io.*;
import java.util.*;

class Main {
    private static int N = 510;
    private static int M = 10010;
    private static int[] backup = new int[N]; // 用于备份之前迭代的dist数组
    private static int[] dist = new int[N]; // 从1号点到 n号点的距离
    private static Node[] list = new Node[M]; // 结构体
    private static int n; // 总点数
    private static int m; // 总边数
    private static int k; // 最多经过k条边
    private static int INF = 0x3f3f3f3f;

    public static void main(String[] args) throws IOException {
        BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
        String[] str1 = bufferedReader.readLine().split(" ");
        n = Integer.parseInt(str1[0]);
        m = Integer.parseInt(str1[1]);
        k = Integer.parseInt(str1[2]);

        for (int i = 0; i < m; i ++) {
            String[] str2 = bufferedReader.readLine().split(" ");
            int x = Integer.parseInt(str2[0]);
            int y = Integer.parseInt(str2[1]);
            int z = Integer.parseInt(str2[2]);
            list[i] = new Node(x, y, z);
        }

        bellman_ford();
    }

    public static void bellman_ford() {
        Arrays.fill(dist, INF);
        dist[1] = 0;

        for (int i = 0; i < k; i ++) {
            //备份dist数组
            backup = Arrays.copyOf(dist, n + 1);
            for (int j = 0; j < m; j ++) {
                Node node = list[j];
                int x = node.x;
                int y = node.y;
                int z = node.z;
                dist[y] = Math.min(dist[y], backup[x] + z);
            }
        }

        if (dist[n] > INF / 2) {
            System.out.println("impossible");
        } else {
            System.out.println(dist[n]);
        }
    }
 }

class Node
{
    int x, y, z;
    public Node(int x,int y,int z)
    {
        this.x = x;
        this.y = y;
        this.z = z;
    }
}

dp题目

一、入门 DP

二、网格图 DP

问：如何思考循环顺序？什么时候要正序枚举，什么时候要倒序枚举？

答：这里有一个通用的做法：盯着状态转移方程，想一想，要计算 f[i] [j]，必须先把 f[i+1] [⋅]算出来，那么只有 i 从大到小枚举才能做到。对于 j来说，由于在计算 f[i] [j]的时候， f[i+1] [⋅]已经全部计算完毕，所以 j无论是正序还是倒序枚举都可以。

2435. 矩阵中和能被 K 整除的路径

定义 f[i] [j] [v] 表示从左上走到 (i,j)，且路径和模 k 的结果为 v 时的路径数。

public int numberOfPaths(int[][] grid, int k) {
        final int mod = (int) 1e9 + 7;
        int m = grid.length, n = grid[0].length;
        int[][][] f = new int[m + 1][n + 1][k];
        f[0][1][0] = 1;
        for(int i=0;i<m;i++){
            for (int j = 0; j < n; j++) {
                for(int v=0;v<k;v++){
                    f[i+1][j+1][(v+grid[i][j])%k]=(f[i + 1][j][v] + f[i][j + 1][v]) % mod;
                }
            }
        }
        return f[m][n][0];
    }

174. 地下城游戏

一句话，本题的难点在于怎么处理血量增加的问题, 增加血量不能为之前的损失提供帮助，只会对后续有帮助。
这意味着从王子救“＊＊＊”的思路想dp是困难的，但是“＊＊＊”救王子的思路dp很好做，从后往前推，当前如果可以治愈，那么当前的最小初始血量就是已经扣除的血量减去治疗量，注意不可以<1。 这意味着过量治疗。

public int calculateMinimumHP(int[][] dungeon) {
    int n = dungeon.length, m = dungeon[0].length;
    int[][] dp = new int[n + 1][m + 1];
    for (int i = 0; i <= n; ++i) {
        Arrays.fill(dp[i], Integer.MAX_VALUE);
    }
    dp[n][m - 1] = dp[n - 1][m] = 1;
    for (int i = n - 1; i >= 0; --i) {
        for (int j = m - 1; j >= 0; --j) {
            int minn = Math.min(dp[i + 1][j], dp[i][j + 1]);
            dp[i][j] = Math.max(minn - dungeon[i][j], 1);
        }
    }
    return dp[0][0];
}

741. 摘樱桃

public int cherryPickup(int[][] grid) {
    int N = 51, INF = Integer.MIN_VALUE;
    int [][][]dp=new int[2*N][N][N];
    int n=grid.length;
    for (int k = 0; k <=2*n ; k++) {
        for (int i=0;i<=n;i++){
            for (int j = 0; j <=n; j++) {
                dp[k][i][j]=INF;
            }
        }
    }
    dp[2][1][1]=grid[0][0];
    for(int k=3;k<=2*n;k++){
        for (int i1 = 1; i1 <= n; i1++) {
            for (int i2 = 1; i2 <= n; i2++) {
                int j1 = k - i1, j2 = k - i2;
                if (j1 <= 0 || j1 > n || j2 <= 0 || j2 > n) continue;
                int A=grid[i1-1][j1-1],B=grid[i2-1][j2-1];
                if(A==-1|B==-1)continue;
                int a = dp[k - 1][i1 - 1][i2], b = dp[k - 1][i1 - 1][i2 - 1], c = dp[k - 1][i1][i2 - 1], d = dp[k - 1][i1][i2];
                int t = Math.max(Math.max(a, b), Math.max(c, d)) + A;
                if (i1 != i2) t += B;
                dp[k][i1][i2] = t;
            }
        }
    }
    return dp[2 * n][n][n] <= 0 ? 0 : dp[2 * n][n][n];
}

三、背包

01背包理论基础

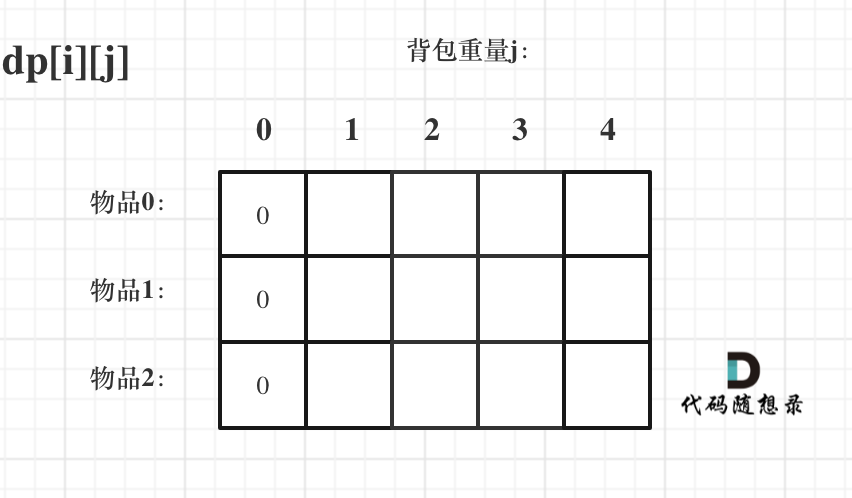
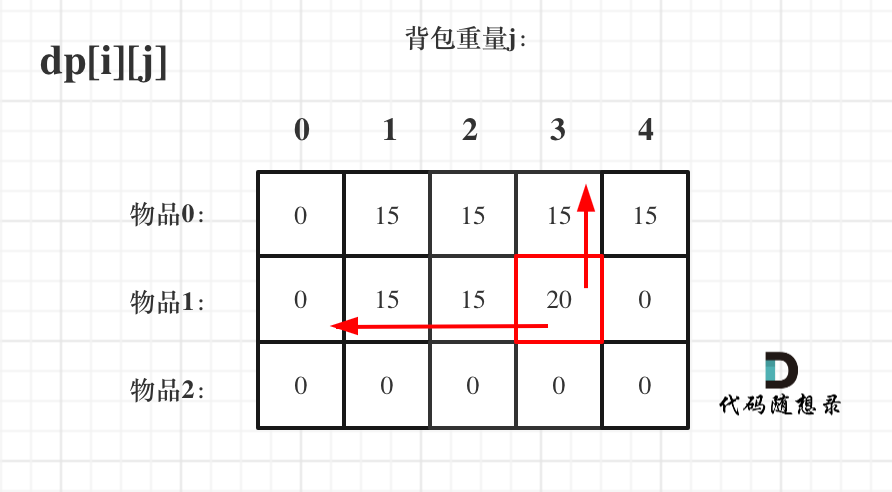
对于背包问题，有一种写法， 是使用二维数组，即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。

for(int i = 1; i < weight.size(); i++) { // 遍历物品
    for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
   }
}

// weight数组的大小 就是物品个数
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
    for(int i = 1; i < weight.size(); i++) { // 遍历物品
        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
    }
}

先遍历背包再遍历物品

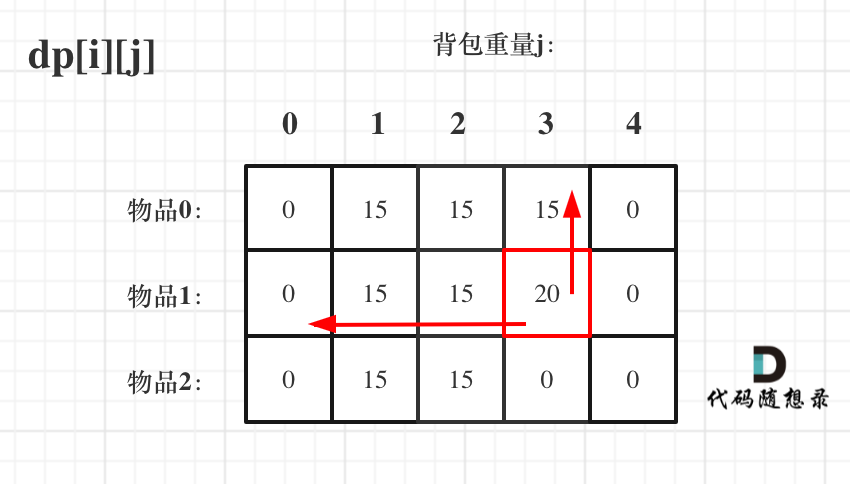
一维dp数组（滚动数组）

dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

这里大家发现和二维dp的写法中，遍历背包的顺序是不一样的！

二维dp遍历的时候，背包容量是从小到大，而一维dp遍历的时候，背包是从大到小。

为什么呢？

倒序遍历是为了保证物品i只被放入一次！。但如果一旦正序遍历了，那么物品0就会被重复加入多次！

再来看看两个嵌套for循环的顺序，代码中是先遍历物品嵌套遍历背包容量，那可不可以先遍历背包容量嵌套遍历物品呢？

不可以！

因为一维dp的写法，背包容量一定是要倒序遍历（原因上面已经讲了），如果遍历背包容量放在上一层，那么每个dp[j]就只会放入一个物品，即：背包里只放入了一个物品。

倒序遍历的原因是，本质上还是一个对二维数组的遍历，并且右下角的值依赖上一层左上角的值，因此需要保证左边的值仍然是上一层的，从右向左覆盖。

完全背包理论基础

每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。

而完全背包的物品是可以添加多次的，所以要从小到大去遍历，即：

// 先遍历物品，再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序是无所谓的！

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。

多重背包

很少出现

四、经典线性 DP

§4.1 最长公共子序列（LCS）

1143. 最长公共子序列

712. 两个字符串的最小ASCII删除和

1035. 不相交的线

72. 编辑距离

§4.2 最长递增子序列（LIS）

300. 最长递增子序列

关键在于d[i]的定义是长度为i的最长上升子序列的末尾元素最小值

//常规做法
public int lengthOfLIS(int[] nums) {
        int result=0;
        int []dp=new int[nums.length];
        Arrays.fill(dp, 1);
        for (int i=0;i<nums.length;i++){
            for (int j=0;j<i;j++){
                if(nums[i]>nums[j])dp[i]=Math.max(dp[i],dp[j]+1);
            }
            if(result<dp[i])result=dp[i];
        }
        return result;
    }

//二分加贪心做法
public int lengthOfLIS(int[] nums) {
        int len = 1, n = nums.length;
        if (n == 0) {
            return 0;
        }
        int[] d = new int[n + 1];
        d[len] = nums[0];
        for (int i = 1; i < n; ++i) {
            if (nums[i] > d[len]) {
                d[++len] = nums[i];
            } else {
                int l = 1, r = len, pos = 0; // 如果找不到说明所有的数都比 nums[i] 大，此时要更新 d[1]，所以这里将 pos 设为 0
                while (l <= r) {
                    int mid = (l + r) >> 1;
                    if (d[mid] < nums[i]) {
                        pos = mid;
                        l = mid + 1;
                    } else {
                        r = mid - 1;
                    }
                }
                d[pos + 1] = nums[i];
            }
        }
        return len;
    }

2111. 使数组 K 递增的最少操作次数

最长递增子序列变式 ,首先根据k进行分组，然后问题转化为求每一组中的最长非递减子序列的长度，用总长度减去子序列的长度即为调整次数。

public int kIncreasing(int[] arr, int k) {
    int ans=0;
    for (int i = 0; i < k; i++) {
        List<Integer> temp=new ArrayList<>();
        int j=i;
        while (j<arr.length){   //分组
            temp.add(arr[j]);
            j+=k;
        }
        if(temp.size()==1) continue;
        int dp[]=new int[temp.size()];
         int maxLen=0;
        for(int num : temp) {           //二分查找
            int low = 0, high = maxLen;
            while(low < high) {
                int mid = low+(high-low)/2;
                if(dp[mid] <= num)
                    low = mid+1;
                else
                    high = mid;
            }
            dp[low] = num;      //更新dp
            if(low == maxLen)
                maxLen++;
        }

        ans+=temp.size()-maxLen;
    }
    return ans;
}

673. 最长递增子序列的个数

两个dp来分别维护最长数组长度 与到第i个结尾时一共有多少个最长的数组

int []dp=new int[nums.length];//最长数组长度
int []count=new int[nums.length];//到第i个结尾时一共有多少个最长的数组
if (nums.length <= 1) return nums.length;
for(int i = 0; i < dp.length; i++) dp[i] = 1;
for(int i = 0; i < count.length; i++) count[i] = 1;
int maxCount=0;
for(int i=1;i<nums.length;i++){
    for(int j=0;j<i;j++){
        if(nums[i]>nums[j]){
            //更新count数组
            if(dp[j] + 1 > dp[i]){
                dp[i] = dp[j] + 1;
                count[i]=count[j];
            }
          else if(dp[j]+1==dp[i]){
                count[i]+=count[j];
            }
            // dp[i]=Math.max(dp[i],dp[j]+1);
        }
        if (dp[i] > maxCount) maxCount = dp[i]; // 记录最长长度
    }
}
int result = 0; // 统计结果
for (int i = 0; i < nums.length; i++) {
    if (maxCount == dp[i]) result += count[i];
}
return result;

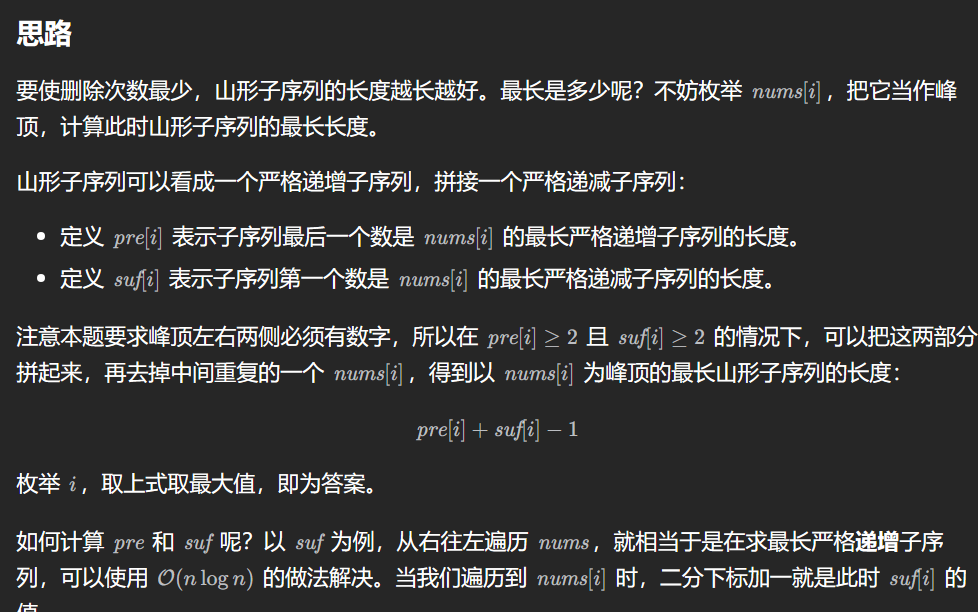
1671. 得到山形数组的最少删除次数

public int minimumMountainRemovals(int[] nums) {
    int n = nums.length;
    int[] pre = getLISArray(nums);
    int[] reversed = reverse(nums);
    int[] suf = getLISArray(reversed);
    suf = reverse(suf);

    int ans = 0;
    for (int i = 0; i < n; ++i) {
        if (pre[i] > 1 && suf[i] > 1) {
            ans = Math.max(ans, pre[i] + suf[i] - 1);
        }
    }

    return n - ans;
}

    public int[] getLISArray(int[] nums) {
        int n = nums.length;
        int[] dp = new int[n];
        Arrays.fill(dp, 1);
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                if (nums[j] < nums[i]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
        }
        return dp;
    }

    public int[] reverse(int[] nums) {
        int n = nums.length;
        int[] reversed = new int[n];
        for (int i = 0; i < n; i++) {
            reversed[i] = nums[n - 1 - i];
        }
        return reversed;
    }

845. 数组中的最长山脉

1964. 找出到每个位置为止最长的有效障碍赛跑路线

此题为最长递增子序列的二分法的应用，找到每次最长的index将其加入res 并实时维护a数组来表示第i长度递增序列的最小的值

public int[] longestObstacleCourseAtEachPosition(int[] obstacles) {
        int n = obstacles.length;
        List<Integer> a = new ArrayList<>();
        int [] res = new int [n];
       for(int i=0;i<n;i++){
        int num=obstacles[i];
        int index=binarysearch(a,num);
        if(index==a.size())a.add(num);
        else{
            a.set(index,num);
        }
        res[i]=index+1;
       }
        return res;
    }
    public int binarysearch(List<Integer> a ,int t){
        int l=0,r=a.size();
        while(l<r){
            int mid=(r-l)/2+l;
            if(a.get(mid)>t){
                r=mid;
            }
            else{
                l=mid+1;
            }
        }
        return l;
    }

2407. 最长递增子序列 II

在求解「上升子序列（IS）」问题时，一般有两种优化方法：

1. 维护固定长度的 IS 的末尾元素的最小值 + 二分优化；

2. 基于值域的线段树、平衡树等数据结构优化。

   此题使用线段树优化

五、状态机 DP

121. 买卖股票的最佳时机

122. 买卖股票的最佳时机 II

123. 买卖股票的最佳时机 III

188. 买卖股票的最佳时机 IV

309. 买卖股票的最佳时机含冷冻期

714. 买卖股票的最佳时机含手续费

六、划分型 DP

§6.1 判定能否划分

2369. 检查数组是否存在有效划分

public boolean validPartition(int[] nums) {
    boolean dp[]=new boolean[nums.length+1];
    dp[0]=true;
    for (int i = 1; i < nums.length; i++) {
        if (dp[i - 1] && nums[i] == nums[i - 1] ||
                i > 1 && dp[i - 2] && (nums[i] == nums[i - 1] && nums[i] == nums[i - 2] ||
                        nums[i] == nums[i - 1] + 1 && nums[i] == nums[i - 2] + 2))
        {
            dp[i+1]=true;
        }
    }
    return dp[nums.length];
}

§6.2 计算划分个数

132. 分割回文串 II

public int minCut(String s) {
    boolean[][]array=new boolean[s.length()][s.length()];
    for(int i=s.length();i>=0;i--){
        for (int j=i;j<s.length();j++){
            if(s.charAt(i)==s.charAt(j)&&(j-i<=1||array[i+1][j-1])){
                array[i][j]=true;
            }
        }
    }
    int []dp=new int[s.length()];
    for(int i=0;i<s.length();i++){
        dp[i]=i;
    }
    for(int i=1;i<s.length();i++){
        if(array[0][i]){
            dp[i]=0;
            continue;
        }
        for(int j=0;j<i;j++){
            if(array[j+1][i]){
                dp[i]=Math.min(dp[i],dp[j]+1);
            }
        }
    }
    return dp[s.length()-1];
}

2707. 字符串中的额外字符

public int minExtraChar(String s, String[] dictionary) {
   int n= s.length();
       int dp[]=new int[n+1];
       Arrays.fill(dp, Integer.MAX_VALUE);
       Map<String,Integer> map=new HashMap<String,Integer>();
       for (String d:
            dictionary) {
           map.put(d,map.getOrDefault(d,0)+1);
       }
       dp[0]=0;
           for (int i = 1; i <=n ; i++) {
           dp[i]=dp[i-1]+1;
           for (int j = i-1; j >=0 ; j--) {
               if(map.containsKey(s.substring(j,i))){
                   dp[i]=Math.min(dp[i],dp[j]);
               }
           }
       }
       return dp[n];
   }

91. 解码方法

其他细节：由于题目存在前导零，而前导零属于无效 item。可以进行特判，但个人习惯往字符串头部追加空格作为哨兵，追加空格既可以避免讨论前导零，也能使下标从 1 开始，简化 f[i-1] 等负数下标的判断。

public int numDecodings(String s) {
    s = " " + s;
    char c[]=s.toCharArray();
    int dp[]=new int [s.length()];
    dp[0]=1;
    for(int i=1;i<s.length();i++){
        int a=c[i]-'0',b=(c[i-1]-'0')*10+(c[i]-'0');
        if(1<=a&&a<=9)dp[i]=dp[i-1];
        if(10<=b&&b<=26)dp[i]+=dp[i-2];
    }
    return dp[s.length()-1];
}

§6.3 约束划分个数

410. 分割数组的最大值

public int splitArray(int[] nums, int m) {
    int max = 0;
    int sum = 0;

    // 计算「子数组各自的和的最大值」的上下界
    for (int num : nums) {
        max = Math.max(max, num);
        sum += num;
    }

    // 使用「二分查找」确定一个恰当的「子数组各自的和的最大值」，
    // 使得它对应的「子数组的分割数」恰好等于 m
    int left = max;
    int right = sum;
    while (left < right) {
        int mid = left + (right - left) / 2;

        int splits = split(nums, mid);
        if (splits > m) {
            // 如果分割数太多，说明「子数组各自的和的最大值」太小，此时需要将「子数组各自的和的最大值」调大
            // 下一轮搜索的区间是 [mid + 1, right]
            left = mid + 1;
        } else {
            // 下一轮搜索的区间是上一轮的反面区间 [left, mid]
            right = mid;
        }
    }
    return left;
}

/***
 *
 * @param nums 原始数组
 * @param maxIntervalSum 子数组各自的和的最大值
 * @return 满足不超过「子数组各自的和的最大值」的分割数
 */
private int split(int[] nums, int maxIntervalSum) {
    // 至少是一个分割
    int splits = 1;
    // 当前区间的和
    int curIntervalSum = 0;
    for (int num : nums) {
        // 尝试加上当前遍历的这个数，如果加上去超过了「子数组各自的和的最大值」，就不加这个数，另起炉灶
        if (curIntervalSum + num > maxIntervalSum) {
            curIntervalSum = 0;
            splits++;
        }
        curIntervalSum += num;
    }
    return splits;
}

1043. 分隔数组以得到最大和

public int maxSumAfterPartitioning(int[] arr, int k) {
    int n=arr.length;
    int dp[]=new int [n+1];
    for(int i=0;i<n;i++){
        for (int j=i,max=0;j>i-k&&j>=0;j--){
             max=Math.max(max,arr[j]);
             dp[i+1]=Math.max(dp[i+1],dp[j]+(i-j+1)*max);
        }
    }
    return dp[n];
}

1745. 分割回文串 IV

此题思路和回文子串相同，用中心扩展法记录有多少个回文子串，然后遍历

public boolean checkPartitioning(String s) {
    int n=s.length();
    boolean dp[][]=new boolean [n][n];
    for (int r = 0; r < n; r++) {
        for (int l = 0; l <=r; l++) {
         if (s.charAt(l) == s.charAt(r) && (r - l <= 2 || dp[l + 1][r - 1])) {
                dp[l][r]=true;
            }
        }
    }
    for(int i=0;i<n;i++){
        if(dp[0][i]){
            for(int j=i+1;j<n-1;j++){
                if(dp[i+1][j]&&dp[j+1][n-1]){
                    return true;
                }
            }
        }
    }

    return false;
}

813. 最大平均值和的分组

public double largestSumOfAverages(int[] nums, int k) {
    int n=nums.length;
    double sum[]=new double [n+1];
    double dp[][]=new double [n+1][k+1];
    for(int i=1;i<=n;i++){
        sum[i]=sum[i-1]+nums[i-1];
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=Math.min(i,k);j++){
            if(j==1){
                dp[i][1]=sum[i]/i;
            }
            else{
                for(int l=2;l<=i;l++){
                    dp[i][j]=Math.max(dp[i][j],dp[l-1][j-1]+(sum[i]-sum[l-1])/(i-l+1));
                }
            }
        }
    }
    return dp[n][k];
}

§6.4 不相交区间

2830. 销售利润最大化

public int maximizeTheProfit(int n, List<List<Integer>> offers) {
        List<int[]>[] groups = new ArrayList[n];
        Arrays.setAll(groups, e -> new ArrayList<>());
        for(List<Integer> offer:offers){
            groups[offer.get(1)].add(new int[]{offer.get(0),offer.get(2)});
        }
        int dp[]=new int [n+1];
        for(int end=0;end<n;end++){
            dp[end+1]=dp[end];
            for(int[]group:groups[end]){
                dp[end+1]=Math.max(dp[end+1],dp[group[0]]+group[1]);
            }
        }
        return dp[n];
    }

2008. 出租车的最大盈利

public long maxTaxiEarnings(int n, int[][] rides) {
    List<int[]>[] groups = new ArrayList[n + 1];
    for (int[] r : rides) {
        int start = r[0], end = r[1], tip = r[2];
        if (groups[end] == null) {
            groups[end] = new ArrayList<>();
        }
        groups[end].add(new int[]{start, end - start + tip});
    }

    long[] f = new long[n + 1];
    for (int i = 2; i <= n; i++) {
        f[i] = f[i - 1];
        if (groups[i] != null) {
            for (int[] p : groups[i]) {
                f[i] = Math.max(f[i], f[p[0]] + p[1]);
            }
        }
    }
    return f[n];
}

public long maxTaxiEarnings(int n, int[][] rides) {
        Arrays.sort(rides, (a, b) -> a[1] - b[1]);
        int m = rides.length;
        long[] dp = new long[m + 1];
        for (int i = 0; i < m; i++) {
            int j = binarySearch1(rides, i, rides[i][0]);
            dp[i + 1] = Math.max(dp[i], dp[j] + rides[i][1] - rides[i][0] + rides[i][2]);
        }
        return dp[m];
    }
    private int binarySearch1(int[][] rides, int right, int target){
        int low =0;
        while (low<right){
            int mid=low+(right-low)/2;
             if(rides[mid][1]>target){
                right=mid;
            }
            else low=mid+1;
        }
        return low;
    }

1235. 规划兼职工作

public int jobScheduling(int[] startTime, int[] endTime, int[] profit) {
        int n = startTime.length;
        int[][] jobs = new int[n][];
        for (int i = 0; i < n; ++i)
            jobs[i] = new int[]{startTime[i], endTime[i], profit[i]};
        Arrays.sort(jobs, (a, b) -> a[1] - b[1]); // 按照结束时间排序
        int[] dp = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            int k = Search(jobs, i - 1, jobs[i - 1][0]);
            dp[i] = Math.max(dp[i - 1], dp[k] + jobs[i - 1][2]);
        }
        return dp[n];
    }
    // 返回 endTime <= upper 的最大下标
    public int Search(int[][] jobs, int right, int target) {
        int left = 0;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (jobs[mid][1] > target) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }

七、其它线性 DP

§7.1 一维

§7.2 特殊子序列

§7.3 矩阵快速幂优化

1137. 第 N 个泰波那契数

552. 学生出勤记录 II

int N = 6;
 int mod = (int)1e9+7;
 long[][] mul(long[][] a, long[][] b) {
     int r = a.length, c = b[0].length, z = b.length;
     long[][] ans = new long[r][c];
     for (int i = 0; i < r; i++) {
         for (int j = 0; j < c; j++) {
             for (int k = 0; k < z; k++) {
                 ans[i][j] += a[i][k] * b[k][j];
         }
     }
     return ans;
 }
 public int checkRecord(int n) {
     long[][] ans = new long[][]{
         {1}, {0}, {0}, {0}, {0}, {0}
     };
     long[][] mat = new long[][]{
         {1, 1, 1, 0, 0, 0},
         {1, 0, 0, 0, 0, 0},
         {0, 1, 0, 0, 0, 0},
         {1, 1, 1, 1, 1, 1},
         {0, 0, 0, 1, 0, 0},
         {0, 0, 0, 0, 1, 0}
     };
     while (n != 0) {
         if ((n & 1) != 0) ans = mul(mat, ans);
         mat = mul(mat, mat);
         n >>= 1;
     }
     int res = 0;
     for (int i = 0; i < N; i++) {
         res += ans[i][0];
         res %= mod;
     }
     return res;
 }                    ans[i][j] %= mod;
}

2851. 字符串转换

public int numberOfWays(String s, String t, long k) {
        int n = s.length();
        int c = kmpSearch(s + s.substring(0, n - 1), t);//避免统计最后一个字母
        long[][] m = {
            {c - 1, c},
            {n - c, n - 1 - c},
        };
        m = pow(m, k);
        return s.equals(t) ? (int) m[0][0] : (int) m[0][1];
    }

    // KMP 模板
    private int[] calcMaxMatch(String s) {
        int[] match = new int[s.length()];
        int c = 0;
        for (int i = 1; i < s.length(); i++) {
            char v = s.charAt(i);
            while (c > 0 && s.charAt(c) != v) {
                c = match[c - 1];
            }
            if (s.charAt(c) == v) {
                c++;
            }
            match[i] = c;
        }
        return match;
    }

    // KMP 模板
    // 返回 text 中出现了多少次 pattern（允许 pattern 重叠）
    private int kmpSearch(String text, String pattern) {
        int[] match = calcMaxMatch(pattern);
        int lenP = pattern.length();
        int matchCnt = 0;
        int c = 0;
        for (int i = 0; i < text.length(); i++) {
            char v = text.charAt(i);
            while (c > 0 && pattern.charAt(c) != v) {
                c = match[c - 1];
            }
            if (pattern.charAt(c) == v) {
                c++;
            }
            if (c == lenP) {
                matchCnt++;
                c = match[c - 1];
            }
        }
        return matchCnt;
    }

    private static final long MOD = (long) 1e9 + 7;

    // 矩阵乘法
    private long[][] multiply(long[][] a, long[][] b) {
        long[][] c = new long[2][2];
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                c[i][j] = (a[i][0] * b[0][j] + a[i][1] * b[1][j]) % MOD;
            }
        }
        return c;
    }

    // 矩阵快速幂
    private long[][] pow(long[][] a, long n) {
        long[][] res = {{1, 0}, {0, 1}};
        for (; n > 0; n /= 2) {//二分法求幂
            if (n % 2 > 0) {
                res = multiply(res, a);
            }
            a = multiply(a, a);
        }
        return res;
    }

八、区间 DP

§8.1 最长回文子序列

516. 最长回文子序列

public int longestPalindromeSubseq(String s) {
    int [][]dp=new int[s.length()][s.length()];
     for (int i = 0; i < s.length(); i++) dp[i][i] = 1;
     for(int i=s.length();i>=0;i--){
        for(int j=i+1;j<s.length();j++){
            if(s.charAt(i)==s.charAt(j))
            dp[i][j]=dp[i+1][j-1]+2;
            else{
                dp[i][j]=Math.max(dp[i+1][j],dp[i][j-1]);
            }
        }
     }
     return dp[0][s.length()-1];
}

730. 统计不同回文子序列

int MOD = (int)1e9+7;
    public int countPalindromicSubsequences(String s) {
        char[] cs = s.toCharArray();
        int n = cs.length;
        int[][] f = new int[n][n];
        int[] L = new int[4], R = new int[4];
        Arrays.fill(L, -1);
        for (int i = n - 1; i >= 0; i--) {
            L[cs[i] - 'a'] = i;
            Arrays.fill(R, -1);
            for (int j = i; j < n; j++) {
                R[cs[j] - 'a'] = j;
                for (int k = 0; k < 4; k++) {
                    if (L[k] == -1 || R[k] == -1) continue;
                    int l = L[k], r = R[k];
                    if (l == r) f[i][j] = (f[i][j] + 1) % MOD;
                    else if (l == r - 1) f[i][j] = (f[i][j] + 2) % MOD;
                    else f[i][j] = (f[i][j] + f[l + 1][r - 1] + 2) % MOD;
                }
            }
        }
        return f[0][n - 1];
    }

1312. 让字符串成为回文串的最少插入次数

public int minInsertions(String s) {
    int n =s.length();
    int [][]dp=new int [n][n];
    for(int i=n-1;i>=0;i--){
        for(int j=i+1;j<n;j++){
            if(s.charAt(i)==s.charAt(j)){
                dp[i][j]=dp[i+1][j-1];
            }
            else{
                dp[i][j]=Math.min(dp[i+1][j],dp[i][j-1])+1;
            }
        }
    }
    return dp[0][n-1];
}

§8.2 其它区间 DP

子串类型可以用中心扩散法优化时间

5. 最长回文子串

public String longestPalindrome(String s) {
        if (s == null || s.length() < 2) {
            return s;
        }
        int strLen = s.length();
        int maxStart = 0;  //最长回文串的起点
        int maxEnd = 0;    //最长回文串的终点
        int maxLen = 1;  //最长回文串的长度

        boolean[][] dp = new boolean[strLen][strLen];

        for (int r = 0; r < strLen; r++) {
            for (int l = 0; l <=r; l++) {
                if (s.charAt(l) == s.charAt(r) && (r - l <= 2 || dp[l + 1][r - 1])) {
                    dp[l][r] = true;
                    if (r - l + 1 > maxLen) {
                        maxLen = r - l + 1;
                        maxStart = l;
                        maxEnd = r;
                    }
                }

            }
        }
        return s.substring(maxStart, maxEnd + 1);

    }

96. 不同的二叉搜索树

public int numTrees(int n) {
    int dp[]=new int[n+1];
    dp[0]=1;
    dp[1]=1;
    for(int i=2;i<=n;i++){
        for(int j=1;j<=i;j++){
            dp[i]+=dp[j-1]*dp[i-j];
        }
    }
    return dp[n];
}

375. 猜数字大小 II

public int getMoneyAmount(int n) {
    int[][] f = new int[n + 10][n + 10];
    for (int len = 2; len <= n; len++) {
        for (int l = 1; l + len - 1 <= n; l++) {
            int r = l + len - 1;
            f[l][r] = 0x3f3f3f3f;
            for (int x = l; x <= r; x++) {
                int cur = Math.max(f[l][x - 1], f[x + 1][r]) + x;
                f[l][r] = Math.min(f[l][r], cur);
            }
        }
    }
    return f[1][n];
}

312. 戳气球

public int maxCoins(int[] nums) {
        int n = nums.length;
        int[] arr = new int[n + 2];
        arr[0] = arr[n + 1] = 1;
        for (int i = 1; i <= n; i++) arr[i] = nums[i - 1];
        int[][] f = new int[n + 2][n + 2];
        for (int len = 3; len <= n + 2; len++) {
            for (int l = 0; l + len - 1 <= n + 1; l++) {
                int r = l + len - 1;
                for (int k = l + 1; k <= r - 1; k++) {
                    f[l][r] = Math.max(f[l][r], f[l][k] + f[k][r] + arr[l] * arr[k] * arr[r]);
                }
            }
        }
        return f[0][n + 1];
    }

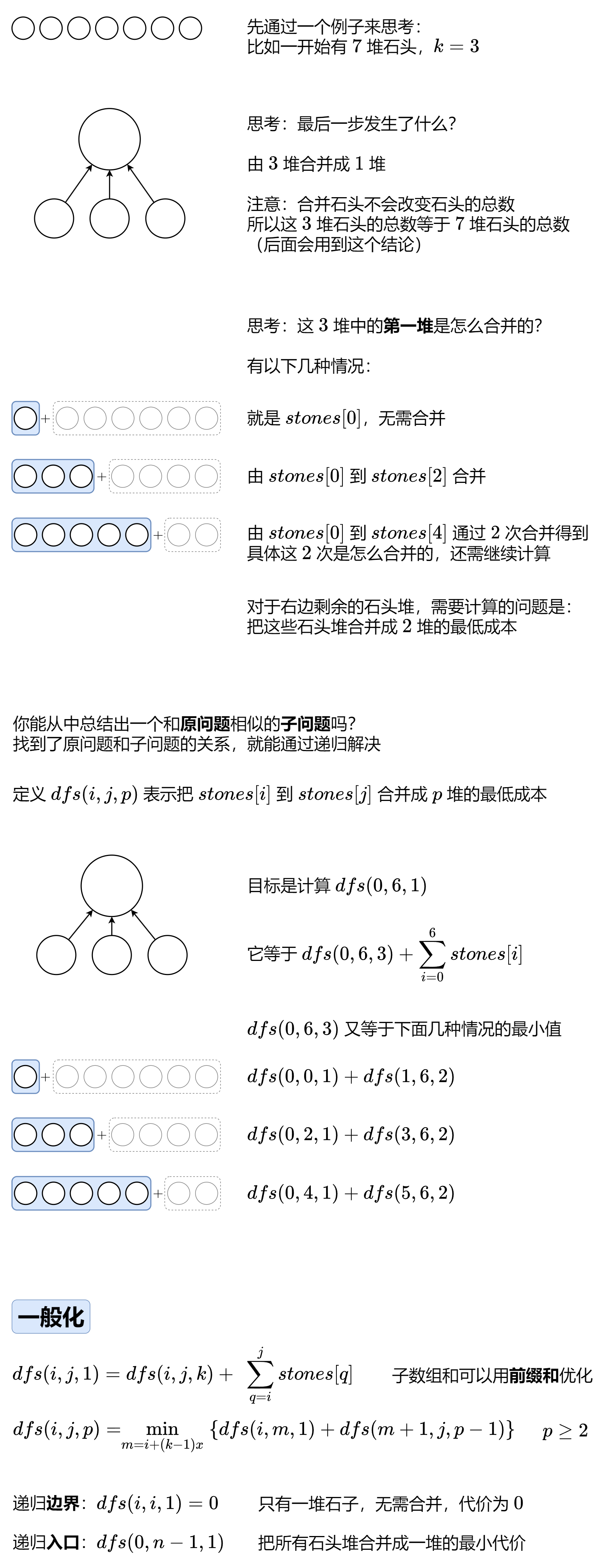
1000. 合并石头的最低成本

public int mergeStones(int[] stones, int k) {
        int n = stones.length;
        if ((n - 1) % (k - 1) > 0) // 无法合并成一堆
            return -1;

        var s = new int[n + 1];
        for (int i = 0; i < n; i++)
            s[i + 1] = s[i] + stones[i]; // 前缀和

        var f = new int[n][n];
        for (int i = n - 1; i >= 0; --i)
            for (int j = i + 1; j < n; ++j) {
                f[i][j] = Integer.MAX_VALUE;
                for (int m = i; m < j; m += k - 1)
                    f[i][j] = Math.min(f[i][j], f[i][m] + f[m + 1][j]);
                if ((j - i) % (k - 1) == 0) // 可以合并成一堆
                    f[i][j] += s[j + 1] - s[i];
            }
        return f[0][n - 1];
    }

九、状态压缩 DP（状压 DP）

§9.1 排列型 ① 相邻无关

§9.2 排列型 ② 相邻相关

§9.3 旅行商问题（TSP）

§9.4 枚举子集的子集

§9.5 其它状压 D

十、数位 DP

2719. 统计整数数目

public int count(String num1, String num2, int minSum, int maxSum) {
        int n = num2.length();
        num1 = "0".repeat(n - num1.length()) + num1; // 补前导零，和 num2 对齐

        int[][] memo = new int[n][Math.min(9 * n, maxSum) + 1];
        for (int[] row : memo) {
            Arrays.fill(row, -1);
        }

        return dfs(0, 0, true, true, num1.toCharArray(), num2.toCharArray(), minSum, maxSum, memo);
    }

    private int dfs(int i, int sum, boolean limitLow, boolean limitHigh, char[] num1, char[] num2, int minSum, int maxSum, int[][] memo) {
        if (sum > maxSum) { // 非法
            return 0;
        }
        if (i == num2.length) {
            return sum >= minSum ? 1 : 0;
        }
        if (!limitLow && !limitHigh && memo[i][sum] != -1) {
            return memo[i][sum];
        }

        int lo = limitLow ? num1[i] - '0' : 0;
        int hi = limitHigh ? num2[i] - '0' : 9;

        int res = 0;
        for (int d = lo; d <= hi; d++) { // 枚举当前数位填 d
            res = (res + dfs(i + 1, sum + d, limitLow && d == lo, limitHigh && d == hi,
                             num1, num2, minSum, maxSum, memo)) % 1_000_000_007;
        }

        if (!limitLow && !limitHigh) {
            memo[i][sum] = res;
        }
        return res;
    }

面试题 17.06. 2出现的次数

char s[];
int dp[][];
public int numberOf2sInRange(int n) {
    s=Integer.toString(n).toCharArray();
    int m=s.length;
    dp=new int [m][m];
    for(int i=0;i<m;i++)Arrays.fill(dp[i],-1);
    return dfs(0,0,true);
}
public int dfs(int i,int count,boolean islimit){
    if(i==s.length)return count;
    if(!islimit&&dp[i][count]>=0)return dp[i][count];
    int res=0;
    for(int j=0,up=islimit?s[i]-'0':9;j<=up;j++){
        res+=dfs(i+1,count+(j==2?1:0),islimit&&j==up);
    }
    if(!islimit)dp[i][count]=res;
    return res;
}

902. 最大为 N 的数字组合

private String[] digits;
    private char s[];
    private int dp[];

    public int atMostNGivenDigitSet(String[] digits, int n) {
        this.digits = digits;
        s = Integer.toString(n).toCharArray();
        dp = new int[s.length];
        Arrays.fill(dp, -1); // dp[i] = -1 表示 i 这个状态还没被计算出来
        return f(0, true, false);
    }

    private int f(int i, boolean isLimit, boolean isNum) {
        if (i == s.length) return isNum ? 1 : 0; // 如果填了数字，则为 1 种合法方案
        if (!isLimit && isNum && dp[i] >= 0) return dp[i]; // 在不受到任何约束的情况下，返回记录的结果，避免重复运算
        var res = 0;
        if (!isNum) // 前面不填数字，那么可以跳过当前数位，也不填数字
            // isLimit 改为 false，因为没有填数字，位数都比 n 要短，自然不会受到 n 的约束
            // isNum 仍然为 false，因为没有填任何数字
            res = f(i + 1, false, false);
        var up = isLimit ? s[i] : '9'; // 根据是否受到约束，决定可以填的数字的上限
        // 注意：对于一般的题目而言，如果此时 isNum 为 false，则必须从 1 开始枚举，由于本题 digits 没有 0，所以无需处理这种情况
        for (var d : digits) { // 枚举要填入的数字 d
            if (d.charAt(0) > up) break; // d 超过上限，由于 digits 是有序的，后面的 d 都会超过上限，故退出循环
            // isLimit：如果当前受到 n 的约束，且填的数字等于上限，那么后面仍然会受到 n 的约束
            // isNum 为 true，因为填了数字
            res += f(i + 1, isLimit && d.charAt(0) == up, true);
        }
        if (!isLimit && isNum) dp[i] = res; // 在不受到任何约束的情况下，记录结果
        return res;
    }

十一、数据结构优化 DP

十二、树形 DP

§12.1 树的直径

int max = 0;
public int diameterOfBinaryTree(TreeNode root) {
    if(root==null){
        return 0;
    }
        dfs1(root);
    return max;
}
public int dfs1(TreeNode root){
    if (root.left == null && root.right == null) {
        return 0;
    }
    int leftSize = root.left == null? 0: dfs1(root.left) + 1;
    int rightSize = root.right == null? 0: dfs1(root.right) + 1;
    max=Math.max(max,leftSize+rightSize);
    return Math.max(leftSize,rightSize);
}

​ 124. 二叉树中的最大路径和

int maxsum=Integer.MIN_VALUE;;
    public int maxPathSum(TreeNode root) {
        dfs(root);
        return maxsum;

    }

    public int dfs(TreeNode root){
        if(root==null)
            return 0;
       int leftgain=Math.max(dfs(root.left),0);
       int rightgain=Math.max(dfs(root.right),0);
       int sum=root.val+leftgain+rightgain;
       maxsum=Math.max(sum,maxsum);
       return root.val + Math.max(leftgain, rightgain);
   }

2246. 相邻字符不同的最长路径

List<Integer>[] g;
 String s;
 int ans;

 public int longestPath(int[] parent, String s) {
     this.s = s;
     var n = parent.length;
     g = new ArrayList[n];
     Arrays.setAll(g, e -> new ArrayList<>());
     for (var i = 1; i < n; i++) g[parent[i]].add(i);

     dfs(0);
     return ans + 1;
 }

 int dfs(int x) {
     var maxLen = 0;
     for (var y : g[x]) {
         var len = dfs(y) + 1;
         if (s.charAt(y) != s.charAt(x)) {
             ans = Math.max(ans, maxLen + len);
             maxLen = Math.max(maxLen, len);
         }
     }
     return maxLen;
 }

§12.2 树上最大独立集

337. 打家劫舍 III

public int rob(TreeNode root) {
    int[] res = robAction1(root);
    return Math.max(res[0],res[1]);
}
    int[] robAction1(TreeNode root) {
        int []res=new int[2];
        if(root==null)return res;
        int []left=robAction1(root.left);
        int []right=robAction1(root.right);
        res[0]=Math.max(left[0],left[1])+Math.max(right[0],right[1]);
        res[1]=root.val+left[0]+right[0];
        return res;
    }

§12.3 树上最小支配集

0:安装摄像头

1：不安装摄像头但是父节点安装摄像头
2：不安装摄像头但是儿子节点安装摄像头

public int minCameraCover(TreeNode root) {
    int[] res = dfs(root);
    return Math.min(res[0], res[2]);
}

private int[] dfs(TreeNode node) {
    if (node == null) {
        return new int[]{Integer.MAX_VALUE / 2, 0, 0}; // 除 2 防止加法溢出
    }
    int[] left = dfs(node.left);
    int[] right = dfs(node.right);
    int choose = Math.min(left[0], left[1]) + Math.min(right[0], right[1]) + 1;
    int byFa = Math.min(left[0], left[2]) + Math.min(right[0], right[2]);
    int byChildren = Math.min(Math.min(left[0] + right[2], left[2] + right[0]), left[0] + right[0]);
    return new int[]{choose, byFa, byChildren};
}

SDOI2006保安站岗

using namespace std;
typedef long long ll;
const int inf=1e9+7;
inline int read()
{
    int p=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){p=p*10+c-'0';c=getchar();}
    return f*p;}
const int maxn=1503;
struct Edge
{
	int from,to;
}p[maxn<<1];
int n,cnt,head[maxn<<1],val[maxn];
int f[maxn][4];
//设状态f[x][0],f[x][1],f[x][2]分别表示
//对于x点,被自己覆盖,被自己的儿子覆盖,被自己的父亲覆盖时
//满足以x为根的子树所有点都被覆盖的最小代价 
inline void add_edge(int x,int y)//加边 
{
	cnt++;
	p[cnt].from=head[x];
	head[x]=cnt;
	p[cnt].to=y;
}
inline void TreeDP(int x,int fa)//树形DP 
{
	f[x][0]=val[x];//初值:选择x点 
	int sum=0,must_need_mincost=inf;
	for(int i=head[x];i;i=p[i].from)
		{
			int y=p[i].to;
			if(y==fa)continue;
			TreeDP(y,x);
			int t=min(f[y][0],f[y][1]);
			f[x][0]+=min(t,f[y][2]);
            //自己被自己覆盖:儿子怎么样都行 
			f[x][2]+=t;
            //自己被父节点覆盖:儿子必须合法,要么选择儿子,要么是儿子被儿子的儿子覆盖 
			//以下是对f[x][1]的转移，请好好理解 
			if(f[y][0]<f[y][1])sum++;
            //如果选择儿子节点更优,选上,计数器sum++，证明选过f[y][0] 
			else must_need_mincost=min(must_need_mincost,f[y][0]-f[y][1]);
			//否则记录一个最小的必须支付代价
            //因为最后要保证x点被y覆盖,必须要找差值最小的,这样才最优 
			f[x][1]+=t;//自己被儿子覆盖,那么儿子必须合法 
		}
	if(!sum)f[x][1]+=must_need_mincost;
	//对于f[x][1]转移:如果一个f[y][0]都没选过,那么必须从差值最小的儿子里面选择一个 
}
int main()
{
	n=read();
	for(int i=1;i<=n;i++)
		{
			int x=read();
			val[x]=read();
			int num=read();
			while(num>0)
				{
					int y=read();
					add_edge(x,y);
					add_edge(y,x);
					num--;
				}
		}
	TreeDP(1,0);
	printf("%d",min(f[1][0],f[1][1]));
	//由于根节点没有父节点,最后答案就是min(f[1][0],f[1][1])
	//即1节点被自己覆盖或者被自己的儿子覆盖 
	return 0;
}

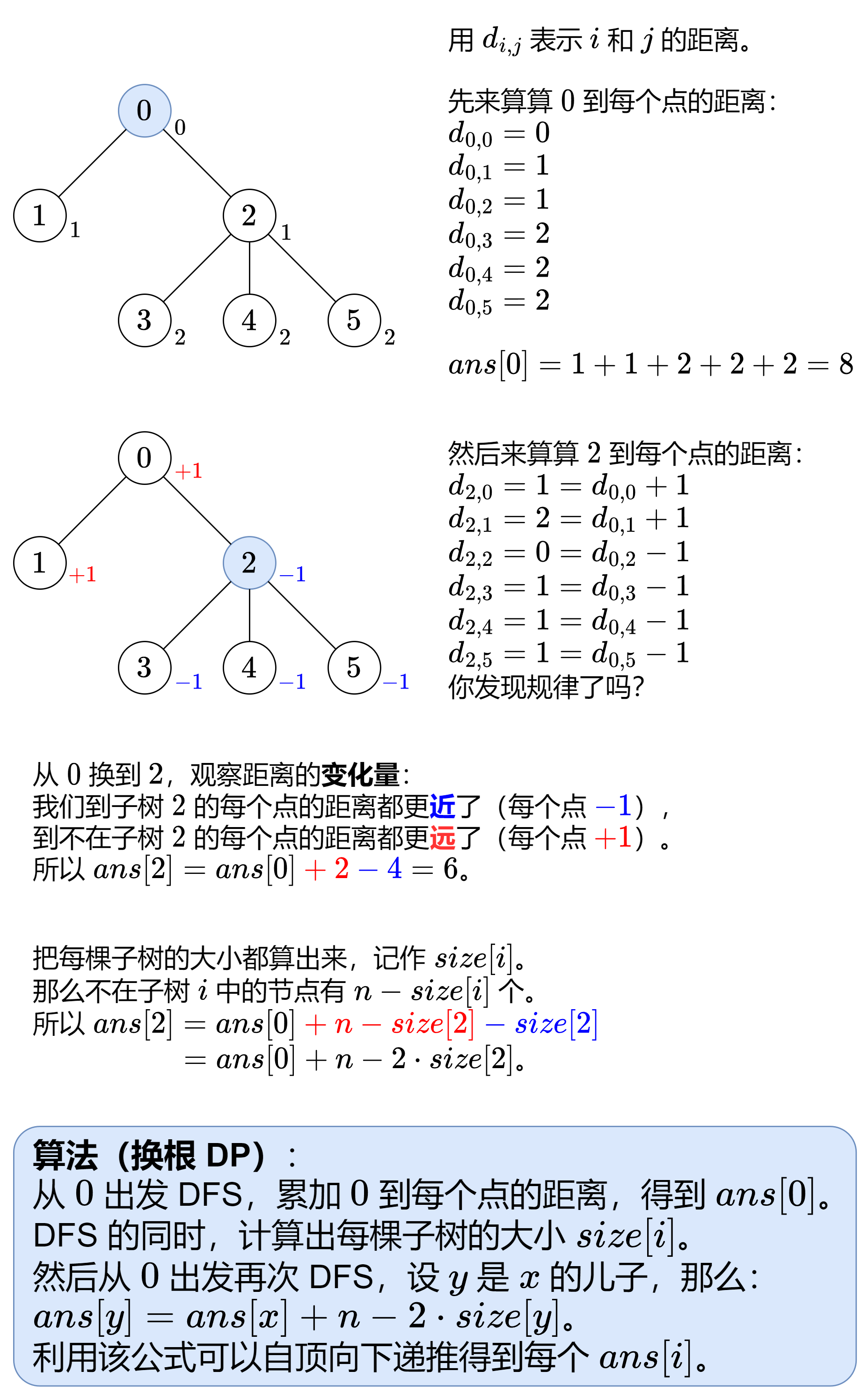
§12.4 换根 DP

834. 树中距离之和

   private List<Integer>[] g;
    private int[] ans, size;
public int[] sumOfDistancesInTree(int n, int[][] edges) {
    g = new ArrayList[n]; // g[x] 表示 x 的所有邻居
    Arrays.setAll(g, e -> new ArrayList<>());
    for (int [] e : edges) {
        int x = e[0], y = e[1];
        g[x].add(y);
        g[y].add(x);
    }
    ans = new int[n];
    size = new int[n];
    dfs(0, -1, 0); // 0 没有父节点
    reroot(0, -1); // 0 没有父节点
    return ans;
}

    private void dfs(int x, int fa, int depth) {
        ans[0] += depth; // depth 为 0 到 x 的距离
        size[x] = 1;
        for (int y : g[x]) { // 遍历 x 的邻居 y
            if (y != fa) { // 避免访问父节点
                dfs(y, x, depth + 1); // x 是 y 的父节点
                size[x] += size[y]; // 累加 x 的儿子 y 的子树大小
            }
        }
    }

    private void reroot(int x, int fa) {
        for (int y : g[x]) { // 遍历 x 的邻居 y
            if (y != fa) { // 避免访问父节点
                ans[y] = ans[x] + g.length - 2 * size[y];
                reroot(y, x); // x 是 y 的父节点
            }
        }
    }

2581. 统计可能的树根数目

private List<Integer>[] times;
   private Set<Long> s = new HashSet<>();
   private int k, res, cnt0;
   
   public int rootCount(int[][] edges, int[][] guesses, int k) {
           this.k = k;
       times = new ArrayList[edges.length + 1];
           Arrays.setAll(times, i -> new ArrayList<>());
           for (int[] e : edges) {
               int x = e[0];
               int y = e[1];
               times[x].add(y);
               times[y].add(x); // 建图
           }

           for (int[] e : guesses) { // guesses 转成哈希表
               s.add((long) e[0] << 32 | e[1]); // 两个 4 字节 int 压缩成一个 8 字节 long
           }

           dfs(0, -1);
           reroot(0, -1, cnt0);
           return res;
       }

       private void dfs(int x, int fa) {
           for (int y : times[x]) {
               if (y != fa) {
                   if (s.contains((long) x << 32 | y)) { // 以 0 为根时，猜对了
                       cnt0++;
                   }
                   dfs(y, x);
               }
           }
       }

       private void reroot(int x, int fa, int cnt) {
           if (cnt >= k) { // 此时 cnt 就是以 x 为根时的猜对次数
               res++;
           }
           for (int y : times[x]) {
               if (y != fa) {
                   int c = cnt;
                   if (s.contains((long) x << 32 | y)) c--; // 原来是对的，现在错了
                   if (s.contains((long) y << 32 | x)) c++; // 原来是错的，现在对了
                   reroot(y, x, c);
               }
           }
   }

图的建立

链式前向星——最完美图解

图的存储方法很多，最常见的除了邻接矩阵、邻接表和边集数组外，还有链式前向星。链式前向星是一种静态链表存储，用边集数组和邻接表相结合，可以快速访问一个顶点的所有邻接点，在算法竞赛中广泛应用。

链式前向星存储包括两种结构：

1. 边集数组：edge[ ]，edge[i]表示第i条边；
2. 头结点数组：head[ ]，head[i]存以i为起点的第一条边的下标(在edge[]中的下标)

struct node{
    int to,next,w;
}edge[maxe];//边集数组，边数一般要设置比maxn*maxn大的数，如果题目有要求除外

int head[maxn];//头结点数组

复制

每一条边的结构，如图所示。

例如，一个无向图，如图所示。

按以下顺序输入每条边的两个端点，建立的链式前向星，过程如下。

1. 输入 1 2 5

创建一条边1—2，权值为5，创建第一条边edge[0]，如图所示。

然后将该边链接到1号结点的头结点中。（初始时head[]数组全部初始化为-1）

即edge[0].next=head[1]; head[1]=0; 表示1号结点关联的第一个条边为0号边，如图所示。图中的虚线箭头仅表示他们之间的链接关系，不是指针。

因为是无向图，还需要添加它的反向边，2—1，权值为5。创建第二条边edge[1]，如图所示。

然后将该边链接到2号结点的头结点中。

即edge[1].next=head[2]; head[2]=1; 表示2号结点关联的第一个条边为1号边，如图所示。

1. 输入 1 4 3

创建一条边1—4，权值为3，创建第3条边edge[2]，如图所示。

然后将该边链接到1号结点的头结点中（头插法）。

即edge[2].next=head[1]; head[1]=2; 表示1号结点关联的第一个条边为2号边，如图所示。

因为是无向图，还需要添加它的反向边，4—1，权值为3。创建第4条边edge[3]，如图所示。

然后将该边链接到4号结点的头结点中。

即edge[3].next=head[4]; head[4]=3; 表示4号结点关联的第一个条边为3号边，如图所示。

1. 依次输入以下三条边，创建的链式前向星，如图所示。

​ 2 3 8

​ 2 4 12

​ 3 4 9

添加一条边u v w的代码如下：

void add(int u,int v,int w){//添加一条边
    edge[cnt].to=v;
    edge[cnt].w=w;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}

复制

如果是有向图，每输入一条边，执行一次add(u,v,w)即可；如果是无向图，则需要执行两次add(u,v,w); add(v,u,w)。

如何使用链式前向星访问一个结点u的所有邻接点呢？

for(int i=head[u];i!=-1;i=edge[i].next){
    int v=edge[i].to; //u的邻接点
    int w=edge[i].w; //u—v的权值
       …
}

复制

链式前向星的特性：

1. 和邻接表一样，因为采用头插法进行链接，所以边输入顺序不同，创建的链式前向星也不同。
2. 对于无向图，每输入一条边，需要添加两条边，互为反向边。例如，输入第一条边1 2 5，实际上添加了两条边，如图所示。

这两条边可以通过互为反向边，可以通过与1的异或运算得到其反向边，0^1=1，1^1=0。也就是说如果一条边的下标为i，则其反向边为i^1。这个特性应用在网络流中非常方便。

3.链式前向星具有边集数组和邻接表的功能，属于静态链表，不需要频繁地创建结点，应用十分灵活。

总代码：

#include<iostream>//创建无向网的链式前向星 
#include<cstring>
using namespace std;
const int maxn=100000+5;
int maxx[maxn],head[maxn];
int n,m,x,y,w,cnt;

struct Edge{
	int to,w,next;
}e[maxn];

void add(int u,int v,int w){//添加一条边u--v 
 	e[cnt].to=v;
 	e[cnt].w=w;
	e[cnt].next=head[u];
	head[u]=cnt++;
} 

void printg(){//输出链式前向星
	cout<<"----------链式前向星如下：----------"<<endl;
	for(int v=1;v<=n;v++){
		cout<<v<<"：  ";
		for(int i=head[v];~i;i=e[i].next){
			int v1=e[i].to,w1=e[i].w;
			cout<<"["<<v1<<" "<<w1<<"]\t";
		}
		cout<<endl;
	}
}

int main(){
	cin>>n>>m;
	memset(head,-1,sizeof(head));
	cnt=0;
	for(int i=1;i<=m;i++){
		cin>>x>>y>>w;
		add(x,y,w);//添加边
		add(y,x,w);//添加反向边 
	}
	printg();
	return 0;
}
/*输入样例
4 5
1 2 5
1 4 3
2 3 8
2 4 12
3 4 9
*/

线段树

线段树的建立

如果题目中给了具体的区间范围，我们根据该范围建立线段树。见题目 区域和检索 - 数组可修改

public void buildTree(Node node, int start, int end) {
    // 到达叶子节点
    if (start == end) {
        node.val = arr[start];
        return ;
    }
    int mid = (start + end) >> 1;
    buildTree(node.left, start, mid);
    buildTree(node.right, mid + 1, end);
    // 向上更新
    pushUp(node);
}
// 向上更新
private void pushUp(Node node) {
    node.val = node.left.val + node.right.val;
}

但是很多时候，题目中都没有给出很具体的范围，只有数据的取值范围，一般都很大，所以我们更常用的是「动态开点」

下面我们手动模拟一下「动态开点」的过程。同样的，也是基于上面的例子 nums = [1, 2, 3, 4, 5]

假设一种情况，最开始只知道数组的长度 5，而不知道数组内每个元素的大小，元素都是后面添加进去的。所以线段树的初始状态如下图所示：(只有一个节点，很孤独！！)

假设此时，我们添加了一个元素 [2, 2]; val = 3。现在线段树的结构如下图所示：

这里需要解释一下，如果一个节点没有左右孩子，会一下子把左右孩子节点都给创建出来，如上图橙色节点所示，具体代码可见方法 pushDown()

两个橙色的叶子节点仅仅只是被创建出来了，并无实际的值，均为 0；而另外一个橙色的非叶子节点，值为 3 的原因是下面的孩子节点的值向上更新得到的

下面给出依次添加剩余节点的过程：(注意观察值的变化！！)

线段树的更新
我看大多数教程都是把更新分为两种：「点更新」和「区间更新」。其实这两种可以合并成一种，「点更新」不就是更新长度为 1 的区间嘛！！

更新区间的前提是找到需要更新的区间，所以和查询的思路很相似

如果我们要把区间 [2, 4] 内的元素都「➕1」

当我们向孩子节点遍历的时候会把「懒惰标记」下推给孩子节点

我们需要稍微修改一下 Node 的数据结构

class Node {
    // 左右孩子节点
    Node left, right;
    // 当前节点值
    int val;
    // 懒惰标记
    int add;
}

基于「动态开点」的前提，我们下推懒惰标记的时候，如果节点不存在左右孩子节点，那么我们就创建左右孩子节点

 * @Description: 线段树（动态开点）

   * @Author: LFool
   * @Date 2022/6/7 09:15
     **/
     public class SegmentTreeDynamic {
     class Node {
         Node left, right;
         int val, add;
     }
     private int N = (int) 1e9;
     private Node root = new Node();
     // 下面来实现更新的函数：
     // 在区间 [start, end] 中更新区间 [l, r] 的值，将区间 [l, r] ➕ val
     // 对于上面的例子，应该这样调用该函数：update(root, 0, 4, 2, 4, 1)
     public void update(Node node, int start, int end, int l, int r, int val) {
       // 找到满足要求的区间
       if (l <= start && end <= r) {
           // 区间节点加上更新值
           // 注意：需要✖️该子树所有叶子节点
           node.val += (end - start + 1) * val;
           // 添加懒惰标记
           // 对区间进行「加减」的更新操作，懒惰标记需要累加，不能直接覆盖
           node.add += val;
           return ;
       }
       int mid = (start + end) >> 1;
       // 下推标记
       // mid - start + 1：表示左孩子区间叶子节点数量
       // end - mid：表示右孩子区间叶子节点数量
       pushDown(node, mid - start + 1, end - mid);
       // [start, mid] 和 [l, r] 可能有交集，遍历左孩子区间
       if (l <= mid) update(node.left, start, mid, l, r, val);
       // [mid + 1, end] 和 [l, r] 可能有交集，遍历右孩子区间
       if (r > mid) update(node.right, mid + 1, end, l, r, val);
       // 向上更新
       pushUp(node);
     }
   //线段树的查询       
   // 在区间 [start, end] 中查询区间 [l, r] 的结果，即 [l ,r] 保持不变
   // 对于上面的例子，应该这样调用该函数：query(root, 0, 4, 2, 4)
    public int query(Node node, int start, int end, int l, int r) {
    // 区间 [l ,r] 完全包含区间 [start, end]
    // 例如：[2, 4] = [2, 2] + [3, 4]，当 [start, end] = [2, 2] 或者 [start, end] = [3, 4]，直接返回
    if (l <= start && end <= r) return node.val;
    // 把当前区间 [start, end] 均分得到左右孩子的区间范围
    // node 左孩子区间 [start, mid]
    // node 左孩子区间 [mid + 1, end]
    int mid = (start + end) >> 1, ans = 0;
    // 下推标记
    pushDown(node, mid - start + 1, end - mid);
    // [start, mid] 和 [l, r] 可能有交集，遍历左孩子区间
    if (l <= mid) ans += query(node.left, start, mid, l, r);
    // [mid + 1, end] 和 [l, r] 可能有交集，遍历右孩子区间
    if (r > mid) ans += query(node.right, mid + 1, end, l, r);
    // ans 把左右子树的结果都累加起来了，与树的后续遍历同理
    return ans;
    }
    // 向上更新
   private void pushUp(Node node) {
       node.val = node.left.val + node.right.val;
   }
//先来实现下推懒惰标记的函数：
// leftNum 和 rightNum 表示左右孩子区间的叶子节点数量
// 因为如果是「加减」更新操作的话，需要用懒惰标记的值✖️叶子节点的数量
private void pushDown(Node node, int leftNum, int rightNum) {
    // 动态开点
    if (node.left == null) node.left = new Node();
    if (node.right == null) node.right = new Node();
    // 如果 add 为 0，表示没有标记
    if (node.add == 0) return ;
    // 注意：当前节点加上标记值✖️该子树所有叶子节点的数量
    node.left.val += node.add * leftNum;
    node.right.val += node.add * rightNum;
    // 把标记下推给孩子节点
    // 对区间进行「加减」的更新操作，下推懒惰标记时需要累加起来，不能直接覆盖
    node.left.add += node.add;
    node.right.add += node.add;
    // 取消当前节点标记
    node.add = 0;
}
}

2407. 最长递增子序列 II - 力扣（LeetCode）

class Solution {
    public int lengthOfLIS(int[] nums, int k) {
        int ans = 0;
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            // 查询区间 [nums[i] - k, nums[i] - 1] 的最值
            int cnt = query(root, 0, N, Math.max(0, nums[i] - k), nums[i] - 1) + 1;
            // 更新，注意这里是覆盖更新，对应的模版中覆盖更新不需要累加，已在下方代码中标注
            update(root, 0, N, nums[i], nums[i], cnt);
            ans = Math.max(ans, cnt);
        }
        return ans;
    }
    // *************** 下面是模版 ***************
    class Node {
        Node left, right;
        int val, add;
    }
    private int N = (int) 1e5;
    private Node root = new Node();
    public void update(Node node, int start, int end, int l, int r, int val) {
        if (l <= start && end <= r) {
            node.val = val; // 不需要累加
            node.add = val; // 不需要累加
            return ;
        }
        pushDown(node);
        int mid = (start + end) >> 1;
        if (l <= mid) update(node.left, start, mid, l, r, val);
        if (r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    }
    public int query(Node node, int start, int end, int l, int r) {
        if (l <= start && end <= r) return node.val;
        pushDown(node);
        int mid = (start + end) >> 1, ans = 0;
        if (l <= mid) ans = query(node.left, start, mid, l, r);
        if (r > mid) ans = Math.max(ans, query(node.right, mid + 1, end, l, r));
        return ans;
    }
    private void pushUp(Node node) {
        node.val = Math.max(node.left.val, node.right.val);
    }
    private void pushDown(Node node) {
        if (node.left == null) node.left = new Node();
        if (node.right == null) node.right = new Node();
        if (node.add == 0) return ;
        node.left.val = node.add;  // 不需要累加
        node.right.val = node.add; // 不需要累加
        node.left.add = node.add;  // 不需要累加
        node.right.add = node.add; // 不需要累加
        node.add = 0;
    }
}

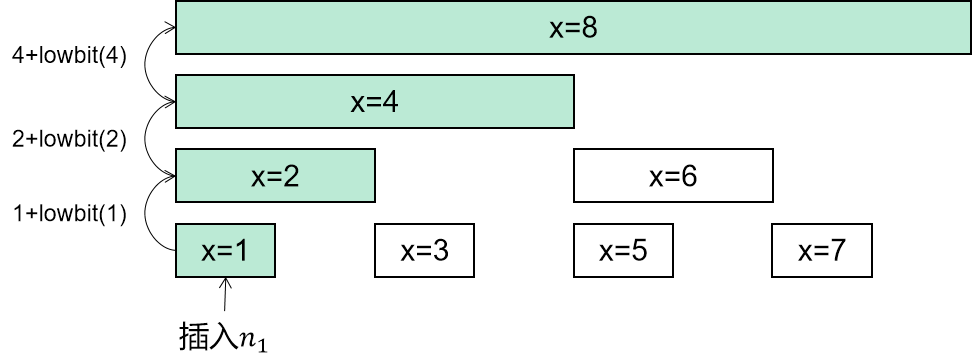
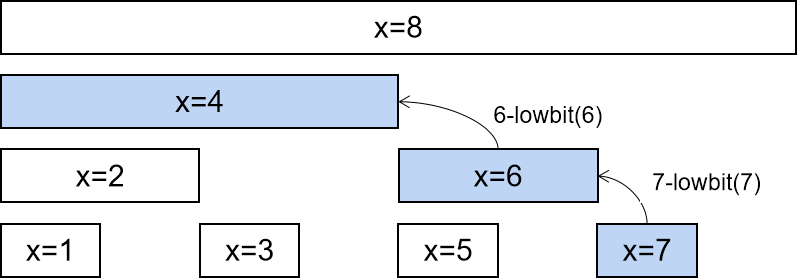
树状数组

307. 区域和检索 - 数组可修改

class NumArray {
    int[] tree;
    int lowbit(int x) {
        return x & -x;
    }
    int query(int x) {
        int ans = 0;
        for (int i = x; i > 0; i -= lowbit(i)) ans += tree[i];
        return ans;
    }
    void add(int x, int u) {
        for (int i = x; i <= n; i += lowbit(i)) tree[i] += u;
    }

    int[] nums;
    int n;
    public NumArray(int[] _nums) {
        nums = _nums;
        n = nums.length;
        tree = new int[n + 1];
        for (int i = 0; i < n; i++) add(i + 1, nums[i]);
    }
    
    public void update(int i, int val) {
        add(i + 1, val - nums[i]);
        nums[i] = val;
    }
    
    public int sumRange(int l, int r) {
        return query(r + 1) - query(l);
    }
}

//模版
// 上来先把三个方法写出来
{
    int[] tree;
    int lowbit(int x) {
        return x & -x;
    }
    // 查询前缀和的方法
    int query(int x) {
        int ans = 0;
        for (int i = x; i > 0; i -= lowbit(i)) ans += tree[i];
        return ans;
    }
    // 在树状数组 x 位置中增加值 u
    void add(int x, int u) {
        for (int i = x; i <= n; i += lowbit(i)) tree[i] += u;
    }
}

// 初始化「树状数组」，要默认数组是从 1 开始
{
    for (int i = 0; i < n; i++) add(i + 1, nums[i]);
}

// 使用「树状数组」：
{   
    void update(int i, int val) {
        // 原有的值是 nums[i]，要使得修改为 val，需要增加 val - nums[i]
        add(i + 1, val - nums[i]); 
        nums[i] = val;
    }
    
    int sumRange(int l, int r) {
        return query(r + 1) - query(l);
    }
}

3072. 将元素分配到两个数组中 II

根据题意，要实现 greaterCount 函数，需要快速查找一个有序结构中，严格大于 val 的元素数量。我们可以使用「树状数组」来实现这个数据结构，其它「线段树」结构也可以实现相同功能。

首先，因为我们只关心数组元素的大小关系，我们可以将数组「离散化」。

然后我们根据题意进行模拟，初始化两个数组和其对应的树，依次遍历原数组中的元素，根据题目条件，将元素加入到对应数组中，并将元素离散化后的数组索引加入到树中。

class TreeArrays{
    private  int []tree;
    public TreeArrays(int n){
        tree=new int[n+1];
    }
    public void add (int i){
        while(i<tree.length){
            tree[i]++;
            i+=i&-i;
        }
    }
    public int get(int i){
        int res=0;
        while(i>0){
            res+=tree[i];
            i-=i&-i;
        }
        return res;
    }
}

class Solution {
    
    public int[] resultArray(int[] nums) {
        int n = nums.length;
        int[] sortedNums = Arrays.copyOf(nums, n);
        Arrays.sort(sortedNums);

        Map<Integer, Integer> index = new HashMap<>();
        for (int i = 0; i < n; i++) {
            index.put(sortedNums[i], i+1);
        }

        List<Integer> arr1 = new ArrayList<>(List.of(nums[0]));
        List<Integer> arr2 = new ArrayList<>(List.of(nums[1]));
        TreeArrays tree1 = new TreeArrays(n);
        TreeArrays tree2 = new TreeArrays(n);
        tree1.add(index.get(nums[0]));
        tree2.add(index.get(nums[1]));

        for (int i = 2; i < n; i++) {
            int count1 = arr1.size() - tree1.get(index.get(nums[i]));
            int count2 = arr2.size() - tree2.get(index.get(nums[i]));
            if (count1 > count2 || (count1 == count2 && arr1.size() <= arr2.size())) {
                arr1.add(nums[i]);
                tree1.add(index.get(nums[i]));
            } else {
                arr2.add(nums[i]);
                tree2.add(index.get(nums[i]));
            }
        }

        int i = 0;
        for (int a: arr1) {
            nums[i++] = a;
        }
        for (int a: arr2) {
            nums[i++] = a;
        }
        return nums;
    }
}

二分强化

五、堆（优先队列）

2530. 执行 K 次操作后的最大分数

自己写一个堆排序

public long maxKelements(int[] nums, int k) {
    buildheap(nums); // 原地堆化（最大堆）
    long ans = 0;
    while (k-- > 0) {
        ans += nums[0]; // 堆顶
        nums[0] = (nums[0] + 2) / 3;
        sink(nums, 0); // 堆化（只需要把 nums[0] 下沉）
    }
    return ans;
} 
public void buildheap(int []num){
    for(int i=num.length/2-1;i>=0;i--){
        sink(num,i);
    }
}
public void sink(int []arr,int index){
    int length=arr.length;
    int leftChild = 2 * index + 1;//左子节点下标
    int rightChild = 2 * index + 2;//右子节点下标
    int present = index;//要调整的节点下标
     //下沉左边
if (leftChild < length && arr[leftChild] > arr[present]) {
    present = leftChild;	
}

//下沉右边
if (rightChild < length && arr[rightChild] > arr[present]) {
    present = rightChild;
}

//如果下标不相等 证明调换过了
if (present != index) {
    //交换值
    int temp = arr[index];
    arr[index] = arr[present];
    arr[present] = temp;

    //继续下沉 在取出头元素后与尾元素交换继续下沉
    sink(arr, present);
    }
}

1834. 单线程 CPU

三个参数排序，先按照到达时间排序，再按照执行时间排序，最后再按照到达顺序排序

public int[] getOrder(int[][] tasks) {
        int n =tasks.length;
        int [][]list=new int[n][3];
        for(int i=0;i<n;i++){
            list[i]=new int []{tasks[i][0],tasks[i][1],i};
        }
        Arrays.sort(list,(a,b)->a[0]-b[0]);
        PriorityQueue<int[]>queue=new PriorityQueue<>((a,b)->{
            if(a[1]!=b[1])return a[1]-b[1];
            return a[2]-b[2];
        });
        int []res=new int[n];
        for (int time = 1, j = 0, idx = 0; idx < n; ) {
            while (j < n && list[j][0] <= time) queue.add(list[j++]);
            if (queue.isEmpty()) {
                time = list[j][0];
            } else {
                int[] cur = queue.poll();
                res[idx++] = cur[2];
                time += cur[1];
            }
        }
        return res;
    }

1792. 最大平均通过率

public double maxAverageRatio(int[][] classes, int extraStudents) {
 PriorityQueue<int[]> pq = new PriorityQueue<int[]>((a, b) -> {
            long val1 = (long) (b[1] + 1) * b[1] * (a[1] - a[0]);
            long val2 = (long) (a[1] + 1) * a[1] * (b[1] - b[0]);
            if (val1 == val2) {
                return 0;
            }
            return val1 < val2 ? 1 : -1;
        });
        for (int[] c : classes) {
            pq.offer(new int[]{c[0], c[1]});
        }

        for (int i = 0; i < extraStudents; i++) {
            int[] arr = pq.poll();
            int pass = arr[0], total = arr[1];
            pq.offer(new int[]{pass + 1, total + 1});
        }

        double res = 0;
        for (int i = 0; i < classes.length; i++) {
            int[] arr = pq.poll();
            int pass = arr[0], total = arr[1];
            res += 1.0 * pass / total;
        }
        return res / classes.length;
    }

2402. 会议室 III

public int mostBooked(int n, int[][] meetings) {
       var cnt = new int[n];
       var idle = new PriorityQueue<Integer>();
       for (var i = 0; i < n; ++i) idle.offer(i);
       var using = new PriorityQueue<Pair<Long, Integer>>((a, b) -> !Objects.equals(a.getKey(), b.getKey()) ? Long.compare(a.getKey(), b.getKey()) : Integer.compare(a.getValue(), b.getValue()));
       Arrays.sort(meetings, (a, b) -> Integer.compare(a[0], b[0]));
       for (var m : meetings) {
           long st = m[0], end = m[1];
           while (!using.isEmpty() && using.peek().getKey() <= st) {
               idle.offer(using.poll().getValue()); // 维护在 st 时刻空闲的会议室
           }
           int id;
           if (idle.isEmpty()) {
               var p = using.poll(); // 没有可用的会议室，那么弹出一个最早结束的会议室（若有多个同时结束的，会弹出下标最小的）
               end += p.getKey() - st; // 更新当前会议的结束时间
               id = p.getValue();
           } else id = idle.poll();
           ++cnt[id];
           using.offer(new Pair<>(end, id)); // 使用一个会议室
       }
       var ans = 0;
       for (var i = 0; i < n; ++i) if (cnt[i] > cnt[ans]) ans = i;
       return ans;
   }

2940. 找到 Alice 和 Bob 可以相遇的建筑

这题关键在于记录下无法跳到的的末尾的位置，然后从这个末尾位置开始使用优先队列从小到排列与每个为的高度值对比求出可以一起跳到的位置

public int[] leftmostBuildingQueries(int[] heights, int[][] queries) {
       int[] ans = new int[queries.length];
       Arrays.fill(ans, -1);
       List<int[]>[] left = new ArrayList[heights.length];
       Arrays.setAll(left, e -> new ArrayList<>());
       for (int qi = 0; qi < queries.length; qi++) {
           int i = queries[qi][0], j = queries[qi][1];
           if (i > j) {
               int temp = i;
               i = j;
               j = temp; // 保证 i <= j
           }
           if (i == j || heights[i] < heights[j]) {
               ans[qi] = j; // i 直接跳到 j
           } else {
               left[j].add(new int[]{heights[i], qi}); // 离线
           }
       }

       PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]);
       for (int i = 0; i < heights.length; i++) { // 从小到大枚举下标 i
           while (!pq.isEmpty() && pq.peek()[0] < heights[i]) {
               ans[pq.poll()[1]] = i; // 可以跳到 i（此时 i 是最小的）
           }
           for (int[] p : left[i]) {
               pq.offer(p); // 后面再回答
           }
       }
       return ans;
   }

§5.3 重排元素

1405. 最长快乐字符串

此类题都是贪心和堆排序结合用堆排序满足贪心优先的想法

public String longestDiverseString(int a, int b, int c) {
       PriorityQueue<int[]> q = new PriorityQueue<>((x,y)->y[1]-x[1]);
       if (a > 0) q.add(new int[]{0, a});
       if (b > 0) q.add(new int[]{1, b});
       if (c > 0) q.add(new int[]{2, c});
       StringBuilder sb = new StringBuilder();
       while (!q.isEmpty()) {
           int[] cur = q.poll();
           int n = sb.length();
           if (n >= 2 && sb.charAt(n - 1) - 'a' == cur[0] && sb.charAt(n - 2) - 'a' == cur[0]) {
               if (q.isEmpty()) break;
               int[] next = q.poll();
               sb.append((char)(next[0] + 'a'));
               if (--next[1] != 0) q.add(next);
               q.add(cur);
           } else {
               sb.append((char)(cur[0] + 'a'));
               if (--cur[1] != 0) q.add(cur);
           }
       }
       return sb.toString();
   }

§5.4 第 K 小/大

264. 丑数 II

int[] nums = new int[]{2,3,5};
    public int nthUglyNumber(int n) {
        PriorityQueue <Long>priorityQueue=new PriorityQueue<>();
        Set<Long>set=new HashSet<>();
        set.add(1L);
        priorityQueue.add(1L);
        for(int i=1;i<=n;i++){
            long temp=priorityQueue.poll();
            if(i==n)return (int)temp;
            for(int num:nums ){
                long x=num*temp;
                if(!set.contains(x)){
                    set.add(x);
                    priorityQueue.add(x);
                }
            }
        }
        return -1;
    }

2386. 找出数组的第 K 大和

public long kSum(int[] nums, int k) {
        int n = nums.length;
        long total = 0;
        for (int i = 0; i < n; i++) {
            if (nums[i] >= 0) {
                total += nums[i];
            } else {
                nums[i] = -nums[i];
            }
        }
        Arrays.sort(nums);
        long ret = 0;
        PriorityQueue<long[]> pq = new PriorityQueue<long[]>((a, b) -> Long.compare(a[0], b[0]));
        pq.offer(new long[]{nums[0], 0});
        for (int j = 2; j <= k; j++) {
            long[] arr = pq.poll();
            long t = arr[0];
            int i = (int) arr[1];
            ret = t;
            if (i == n - 1) {
                continue;
            }
            pq.offer(new long[]{t + nums[i + 1], i + 1});
            pq.offer(new long[]{t - nums[i] + nums[i + 1], i + 1});
        }
        return total - ret;
    }

§5.5 反悔堆

LCP 30. 魔塔游戏

1.初始化血量 hp=1。
2.从左到右遍历数组，把小于 0 的数丢到一个小根堆中。
3.遍历的同时，把 nums[i] 加到 hp 中。如果 hp<1，那么弹出堆顶，hp 减去堆顶，相当于把之前扣掉的血重新加回来。同时把调整次数增加一。注意如果 hp<1，那么必然是由当前这个小于 0 的 nums[i] 导致的，这一保证了此时堆不为空，二保证了 hp 减去堆顶后必然可以恢复成正数，因为堆顶不会比 nums[i] 还大。
4返回调整次数。

public int magicTower(int[] nums) {
        PriorityQueue<Integer>queue=new PriorityQueue<>();
        long cur=1;
        int back=0;
        int res=0;
        for(int num:nums){
            if(num<0)queue.offer(num);
            cur+=num;
            if(cur<=0){
                res++;
                int n=queue.poll();
                cur-=n;
                back+=n;
            }
        }
        cur+=back;
        return cur>0?res:-1;
    }

630. 课程表 III

看上去，找不到一个合适的贪心策略。别放弃！顺着这个思路，如果我们可以「反悔」呢？

按照 lastDay 从小到大排序，然后遍历 courses。比如先上完 duration=7 的课和 duration=10 的课，后面遍历到了 duration=4 的课，但受到 lastDay 的限制，无法上 duration=4 的课。此时，我们可以「撤销」前面 duration 最长的课，也就是 duration=10 的课，这样就可以上 duration=4 的课了！虽然能上完的课程数目没有变化，但是由于我们多出了 10−4=6 天时间，在后续的遍历中，更有机会上完更多的课程。

在上面的讨论中，我们需要维护一个数据结构，来帮助我们快速找到 duration 最长的课程。这可以用最大堆解决。

public int scheduleCourse(int[][] courses) {
       Arrays.sort(courses, (a, b) -> a[1] - b[1]); // 按照 lastDay 从小到大排序
       PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> b - a); // 最大堆
       int day=0;
       for(int []course:courses){
           int duration = course[0], lastDay = course[1];
           if(day+duration<=lastDay){
               day+=duration;
               pq.offer(duration);
           }
           else if(!pq.isEmpty()&&duration<pq.peek()){
               day-=pq.poll()-duration;
               pq.offer(duration);
           }
       }
       return pq.size();
   }

3049. 标记所有下标的最早秒数 II

周赛题参见周赛

§5.6 懒删除堆

2349. 设计数字容器系统

用最小堆堆存储改数字曾经存在于那个数据组中，然后再判断当前数据组是否存储这个数字如果存储返回

class NumberContainers {
        Map<Integer,Integer>map=new HashMap<>();
        Map<Integer,PriorityQueue<Integer>>ms=new HashMap<>();
    public NumberContainers() {

    }
    
    public void change(int index, int number) {
        map.put(index,number);
        ms.computeIfAbsent(number, k -> new PriorityQueue<>()).offer(index);
    }
    
    public int find(int number) {
        var q=ms.get(number); 
        if(q==null)return -1;
        while(!q.isEmpty()&&map.get(q.peek())!=number)q.poll();
        return q.isEmpty()?-1:q.peek();
    }
}

§5.7 对顶堆

295. 数据流的中位数

class MedianFinder {


    Queue<Integer>min=new PriorityQueue<>();
    Queue<Integer>max=new PriorityQueue<>();
    public MedianFinder() {
        min = new PriorityQueue<Integer>((a, b) -> (b - a));
        max = new PriorityQueue<Integer>((a, b) -> (a - b));
    }

    public void addNum(int num) {
        if(min.isEmpty()||num<=min.peek()){
            min.offer(num);
            if(max.size()+1<min.size()){
                max.offer(min.poll());
            }
        }
        else {
            max.offer(num);
            if(min.size()<max.size()){
                min.offer(max.poll());
            }
        }
    }

    public double findMedian() {
        if(max.size()<min.size()){
            return min.peek();
        }
        return (max.peek()+min.peek())/2.0;
    }
}

2102. 序列顺序查询

295. 数据流的中位数的变种题
     小根堆的最小值 >= 大根堆的最大值
     295题求中间的一个或两个数，保证两个堆的大小差距不超过1即可
     本题求第i个数(i等于get()的次数)，保证小根堆的大小等于i即可

class SORTracker {
    List<String> names = new ArrayList<>();
    List<Integer> scores = new ArrayList<>();
    Comparator<Integer> comparator = Comparator.comparing(scores::get)
            .thenComparing(Comparator.comparing(names::get).reversed());
    Queue<Integer> minHeap = new PriorityQueue<>(comparator);
    Queue<Integer> maxHeap = new PriorityQueue<>(comparator.reversed());

/*
//使用 Lambda 表达式改写 Comparator
Comparator<Integer> comparator = (i1, i2) -> {
    int scoreComparison = scores.get(i1).compareTo(scores.get(i2));
    if (scoreComparison != 0) {
        return scoreComparison;
    }
    // If scores are the same, compare names in reversed order
    return names.get(i2).compareTo(names.get(i1));
};

//重写 compare 方法
Comparator<Integer> comparator = new Comparator<Integer>() {
    @Override
    public int compare(Integer i1, Integer i2) {
        int scoreComparison = scores.get(i1).compareTo(scores.get(i2));
        if (scoreComparison != 0) {
            return scoreComparison;
        }
       // If scores are the same, compare names in reversed order
        return names.get(i2).compareTo(names.get(i1));
    }
};
*/

Queue<Integer> minHeap = new PriorityQueue<>(comparator);
Queue<Integer> maxHeap = new PriorityQueue<>(comparator.reversed());    Comparator<Integer> comparator = new Comparator<Integer>() {
    @Override
    public int compare(Integer i1, Integer i2) {
        int scoreComparison = scores.get(i1).compareTo(scores.get(i2));
        if (scoreComparison != 0) {
            return scoreComparison;
        }
        // If scores are the same, compare names in reversed order
        return names.get(i2).compareTo(names.get(i1));
    }
};

Queue<Integer> minHeap = new PriorityQueue<>(comparator);
Queue<Integer> maxHeap = new PriorityQueue<>(comparator.reversed());
    public SORTracker() {
    }

    public void add(String name, int score) {
        names.add(name);
        scores.add(score);
        minHeap.offer(names.size() - 1);
        maxHeap.offer(minHeap.poll());
    }

    public String get() {
        minHeap.offer(maxHeap.poll());
        return names.get(minHeap.peek());
    }
}

六、字典树（trie）

212. 单词搜索 II

 int[][] dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};

    public List<String> findWords(char[][] board, String[] words) {
        Trie trie = new Trie();
        for (String word : words) {
            trie.insert(word);
        }

        Set<String> ans = new HashSet<String>();
        for (int i = 0; i < board.length; ++i) {
            for (int j = 0; j < board[0].length; ++j) {
                dfs(board, trie, i, j, ans);
            }
        }

        return new ArrayList<String>(ans);
    }

    public void dfs(char[][] board, Trie now, int i1, int j1, Set<String> ans) {
        if (!now.children.containsKey(board[i1][j1])) {
            return;
        }
        char ch = board[i1][j1];
        Trie nxt = now.children.get(ch);
        if (!"".equals(nxt.word)) {
            ans.add(nxt.word);
            nxt.word = "";
        }

        if (!nxt.children.isEmpty()) {
            board[i1][j1] = '#';
            for (int[] dir : dirs) {
                int i2 = i1 + dir[0], j2 = j1 + dir[1];
                if (i2 >= 0 && i2 < board.length && j2 >= 0 && j2 < board[0].length) {
                    dfs(board, nxt, i2, j2, ans);
                }
            }
            board[i1][j1] = ch;
        }

        if (nxt.children.isEmpty()) {
            now.children.remove(ch);
        }
    }
}

class Trie {
    String word;
    Map<Character, Trie> children;
    boolean isWord;

    public Trie() {
        this.word = "";
        this.children = new HashMap<Character, Trie>();
    }

    public void insert(String word) {
        Trie cur = this;
        for (int i = 0; i < word.length(); ++i) {
            char c = word.charAt(i);
            if (!cur.children.containsKey(c)) {
                cur.children.put(c, new Trie());
            }
            cur = cur.children.get(c);
        }
        cur.word = word;
    }

3045. 统计前后缀下标对 II

将字符的前n位和倒数n位一起拼成一个组，这个就可以将该组作为一个前缀树节点，然后依次判断该组出现的次数累加即可

class Trie{
    Map<Integer,Trie>son=new HashMap<>();
    int cnt;
}

class Solution {
    public long countPrefixSuffixPairs(String[] words) {
        long res=0;
        Trie t=new Trie();
        for(String s :words){
            char c[]=s.toCharArray();
            int n=c.length;
            Trie cur=t;
            for(int i=0;i<n;i++){
                int pos=(c[i]-'a')<<5|(c[n-1-i]-'a');
                cur=cur.son.computeIfAbsent(pos, k->new Trie());
                res+=cur.cnt;
            }
            cur.cnt++;
        }
        return res;
    }
}

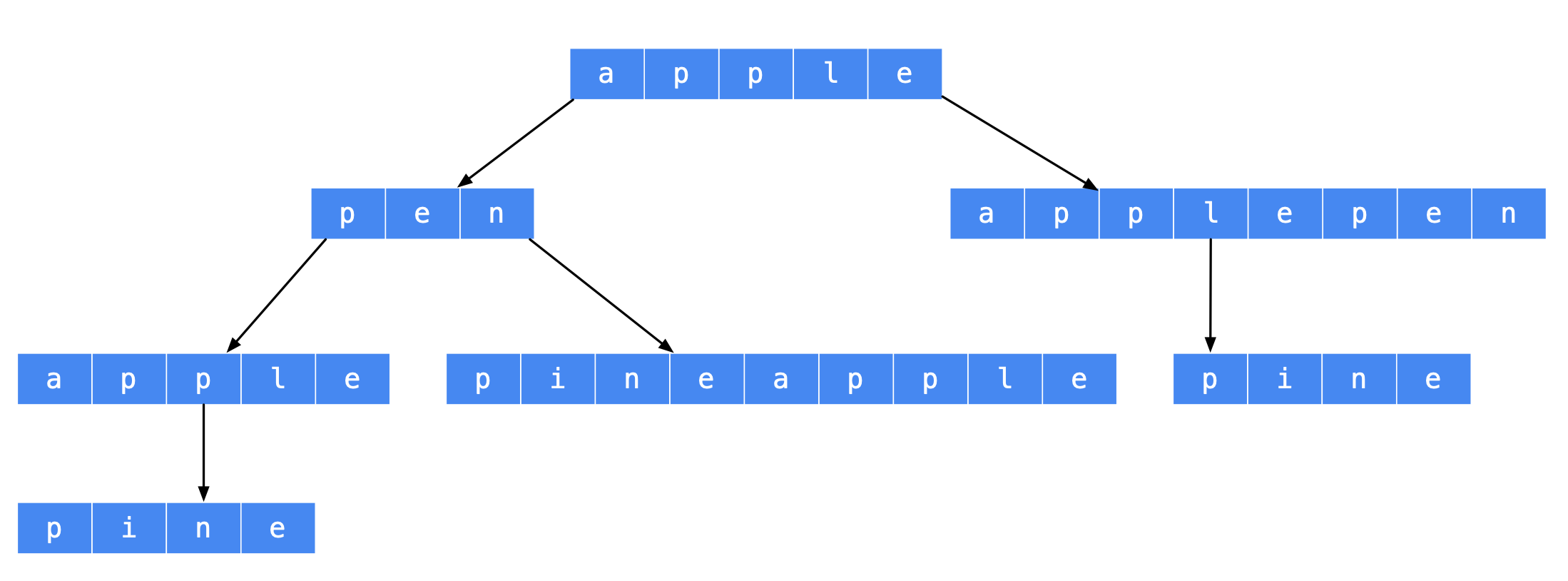
§6.3 字典树优化 DP

140. 单词拆分 II

此题先将类似于单词拆分1 记录这个字符串能否被拆分成对应的单词set，然后再从后往前回溯便利每个dp[i]==true 的单词求得集合

public List<String> wordBreak(String s, List<String> wordDict) {
    Set<String>set=new HashSet<>(wordDict);
    int n=s.length();
    boolean dp[]=new boolean[n+1];
    dp[0]=true;
    for(int i=1;i<=n;i++){
        for(int j=i-1;j>=0;j--){
            if(set.contains(s.substring(j,i))&&dp[j]){
                dp[i]=true;
                break;
            }
        }
    }
    List<String> res = new ArrayList<>();
    if (dp[n]) {
        Deque<String> path = new ArrayDeque<>();
        dfs(s, n, set, dp, path, res);
        return res;
    }
    return res;
}
private void dfs(String s ,int n,Set<String>set,boolean dp[],
Deque<String>path,List<String> res){
    if(n==0){
        res.add(String.join(" ", path));
        return;
    }
        for(int j=n-1;j>=0;j--){
            String word=s.substring(j,n);
            if(set.contains(word)&&dp[j]){
                path.addFirst(word);
                dfs(s, j, set, dp, path, res);
                path.removeFirst(); 
            }
        }
}

七、并查集

737. 句子相似性 II

public boolean areSentencesSimilarTwo(String[] sentence1, String[] sentence2, List<List<String>> similarPairs) {   
        if (sentence1.length != sentence2.length) return false;
        Map<String, Integer> index = new HashMap();
        int count = 0;
        sim s=new sim(2*similarPairs.size());
        for(List<String>pair:similarPairs){
            for(String p:pair){
                if(!index.containsKey(p)){
                    index.put(p,count++);
                }
            }
            sim.union(index.get(pair.get(0)),index.get(pair.get(1)));
        }
        for(int i=0;i<sentence1.length;i++){
            String s1=sentence1[i],s2=sentence2[i];
            if(s1.equals(s2))continue;
            if(!index.containsKey(s1)||!index.containsKey(s2)
            ||sim.find(index.get(s1))!=sim.find(index.get(s2)))
            return false;
        }
        return true;
    }
}

class sim {
    static int parent [];
    public sim(int n){
        parent=new int[n];
        for(int i=0;i<n;i++){
            parent[i]=i;
        }
    }
    public static int find(int x){
        if(parent[x]!=x)parent[x]=find(parent[x]);
        return parent[x];
    }
    public static void union(int x,int y){
        parent[find(x)]=find(y);
    }
}

765. 情侣牵手

首先，我们总是以「情侣对」为单位进行设想：

当有两对情侣相互坐错了位置，ta们两对之间形成了一个环。需要进行一次交换，使得每队情侣独立（相互牵手）

如果三对情侣相互坐错了位置，ta们三对之间形成了一个环，需要进行两次交换，使得每队情侣独立（相互牵手）

如果四对情侣相互坐错了位置，ta们四对之间形成了一个环，需要进行三次交换，使得每队情侣独立（相互牵手）

也就是说，如果我们有 k 对情侣形成了错误环，需要交换 k - 1 次才能让情侣牵手。

于是问题转化成 n / 2 对情侣中，有多少个这样的环。

可以直接使用「并查集」来做。

由于 0和1配对、2和3配对 … 因此互为情侣的两个编号除以 2 对应同一个数字，可直接作为它们的「情侣组」编号：

public int minSwapsCouples(int[] row) {
        int n=row.length;
        int t=n/2;
        int f[]=new int[t];
        
        for (int i = 0; i < t; i++) {
            f[i]=i;
        }
        for (int i = 0; i < n; i+=2) {
            int x=row[i]/2;
            int y=row[i+1]/2;
            add(f,x,y);
        }
        Map<Integer, Integer> map = new HashMap<Integer, Integer>();
        for (int i = 0; i < t; i++) {
            int fx = getf(f, i);
            map.put(fx, map.getOrDefault(fx, 0) + 1);
        }
        int res=0;
        for (Map.Entry<Integer,Integer> entry:map.entrySet()) {
            res+=entry.getValue()-1;
        }
        return res;
    }
    public int getf(int[] f, int x) {
        if (f[x] == x) {
            return x;
        }
        f[x]=getf(f,f[x]);
        return f[x];
    }
    public void add(int[] f,int x,int y){
        int fx=getf(f,x);
        int fy=getf(f,y);
        f[fx]=fy;
    }


//简化写法
    int[] p = new int[70];
    public int minSwapsCouples(int[] row) {
        int n=row.length, m=n/2;
        for(int i=0;i<m;i++){
            p[i]=i;
        }
        for(int i=0;i<n;i+=2){
            union(row[i]/2, row[i+1]/2);
        }
        int res=0;
        for(int i=0;i<m;i++){
            if(i!=find(i))res++;
        }
        return res;
    }
    public int  find(int x){
        if(p[x]!=x)p[x]=find(p[x]);
        return p[x];
    }
    public void union(int x,int y){
        p[find(x)]=find(y);
    }

2709. 最大公约数遍历

待定

§7.3 公因数并查集

2709. 最大公约数遍历

将每个数与自己的公因数相连，再遍历每个数，如果不相同则无法连接

class Solution {
 public boolean canTraverseAllPairs(int[] nums) {
        if (nums.length == 1) {
            return true;
        }
        int maxNum = 0;
        for (int num : nums) {
            if (num == 1) {
                return false;
            }
            maxNum = Math.max(maxNum, num);
        }
        UnionFind uf = new UnionFind(maxNum + 1);
        for (int num : nums) {
            for (int i = 2; i * i <= num; i++) {
                if (num % i == 0) {
                    uf.union(num, i);
                    uf.union(num, num / i);
                }
            }
        }
        int root = 0;
        for (int num : nums) {
            int currRoot = uf.find(num);
            if (root == 0) {
                root = currRoot;
            } else if (currRoot != root) {
                return false;
            }
        }
        return true;
    }

}
class UnionFind {
    private int[] parent;
    private int[] rank;

    public UnionFind(int n) {
        parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
        rank = new int[n];
    }

    public void union(int x, int y) {
        int rootx = find(x);
        int rooty = find(y);
        if (rootx != rooty) {
            if (rank[rootx] > rank[rooty]) {
                parent[rooty] = rootx;
            } else if (rank[rootx] < rank[rooty]) {
                parent[rootx] = rooty;
            } else {
                parent[rooty] = rootx;
                rank[rootx]++;
            }
        }
    }

    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }
}

§7.4 数组上的并查集

1488. 避免洪水泛滥

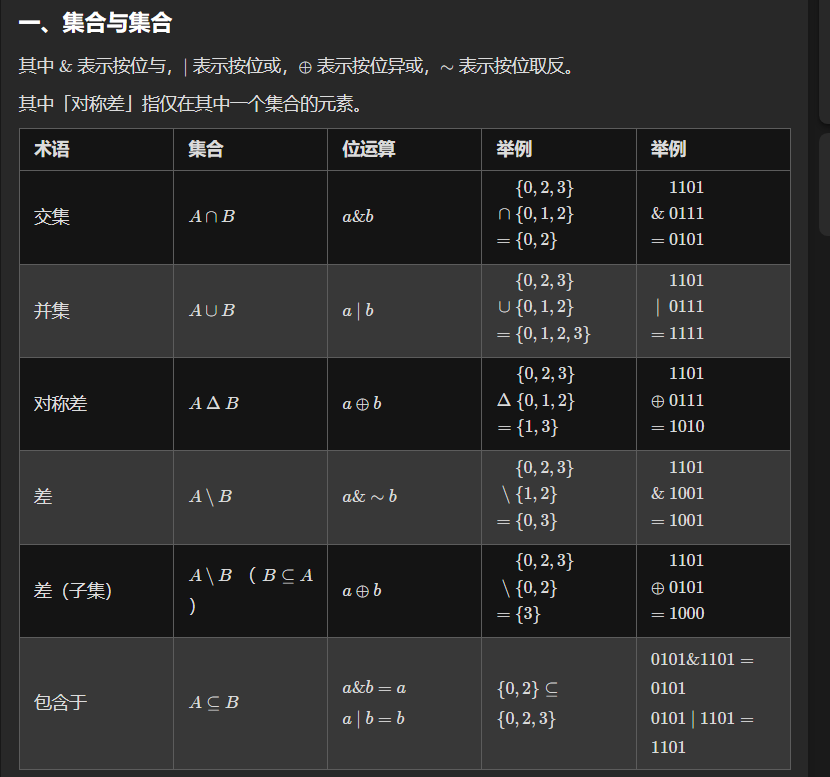
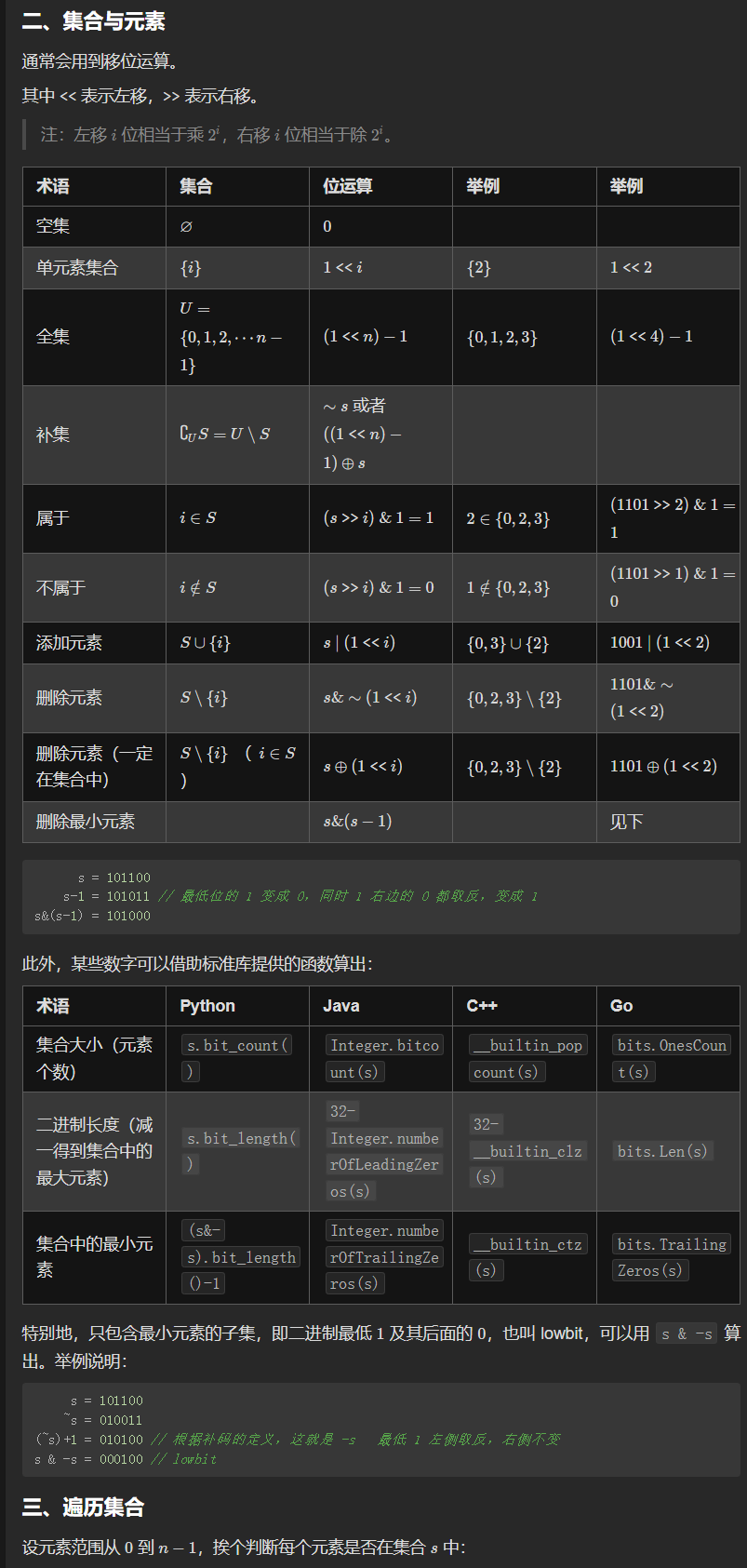
从集合论到位运算，常见位运算技巧分类总结

三、遍历集合

for (int i = 0; i < n; i++) {
    if (((s >> i) & 1) == 1) { // i 在 s 中
        // 处理 i 的逻辑
    }
}

四、枚举集合

for (int s = 0; s < (1 << n); s++) {
    // 处理 s 的逻辑
}

for (int sub = s; sub > 0; sub = (sub - 1) & s) {
    // 处理 sub 的逻辑
}

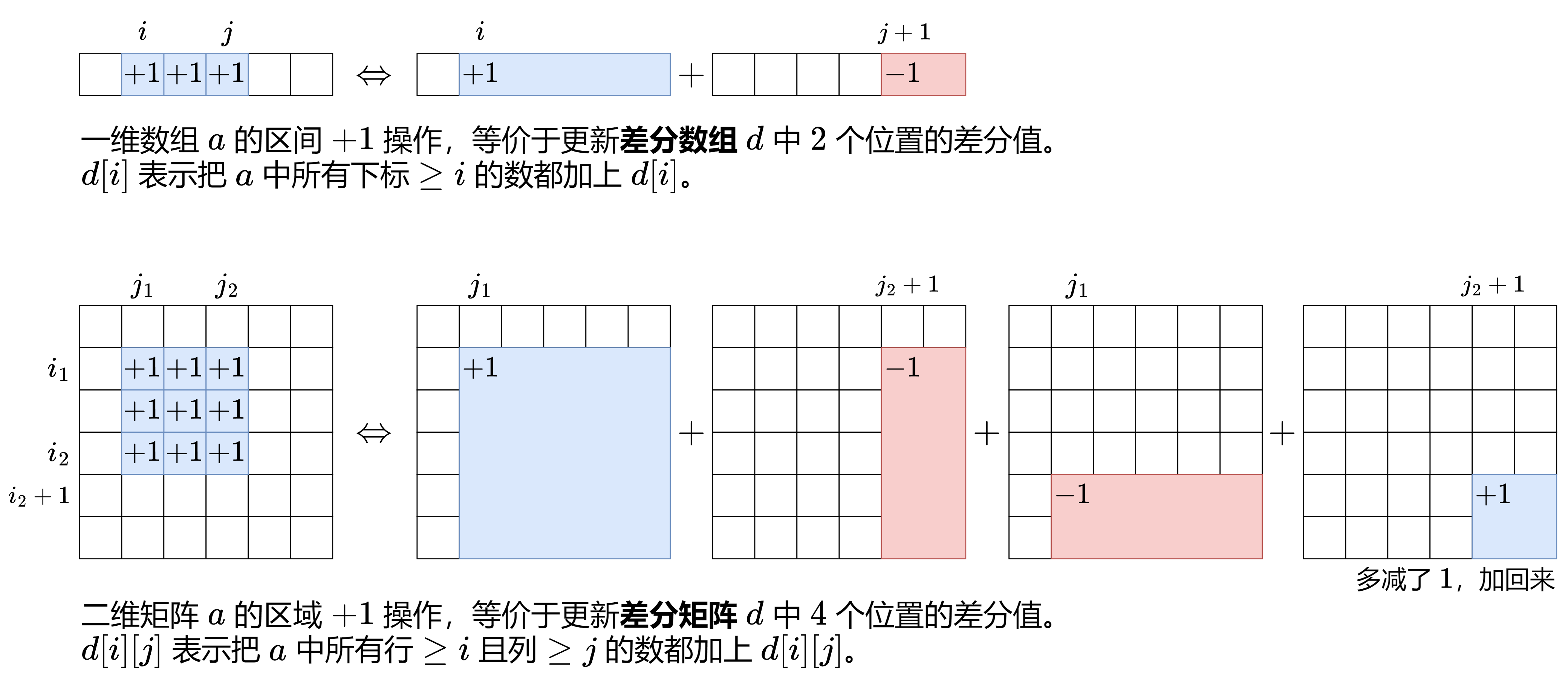
八、差分数组

1094. 拼车

   public boolean carPooling(int[][] trips, int capacity) {
int[] d = new int[1001];
       for (int[] t : trips) {
           int num = t[0], from = t[1], to = t[2];
           d[from] += num;
           d[to] -= num;
       }
       int s = 0;
       for (int v : d) {
           s += v;
           if (s > capacity) {
               return false;
           }
       }
       return true;
   }

2848. 与车相交的点

public int numberOfPoints(List<List<Integer>> nums) {
    int maxend=0;
    for(List<Integer>list:nums){
        maxend =Math.max(maxend,list.get(1));
    }
    int diff[]=new int[maxend+2];
    for(List<Integer>list:nums){
        diff[list.get(0)]++;
        diff[list.get(1)+1]--;
    }
    int res=0;
    int sum=0;
    for(int d:diff){
        sum+=d;
        if(sum>0){
            res++;
        }
    }
    return res;
}

一维差分的思想可以推广至二维，请点击图片放大查看：

2132. 用邮票贴满网格图

class Solution {
    public boolean possibleToStamp(int[][] grid, int stampHeight, int stampWidth) {
        int m = grid.length;
        int n = grid[0].length;

        // 1. 计算 grid 的二维前缀和
        int[][] s = new int[m + 1][n + 1];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + grid[i][j];
            }
        }

        // 2. 计算二维差分
        // 为方便第 3 步的计算，在 d 数组的最上面和最左边各加了一行（列），所以下标要 +1
        int[][] d = new int[m + 2][n + 2];
        for (int i2 = stampHeight; i2 <= m; i2++) {
            for (int j2 = stampWidth; j2 <= n; j2++) {
                int i1 = i2 - stampHeight + 1;
                int j1 = j2 - stampWidth + 1;
                if (s[i2][j2] - s[i2][j1 - 1] - s[i1 - 1][j2] + s[i1 - 1][j1 - 1] == 0) {
                    d[i1][j1]++;
                    d[i1][j2 + 1]--;
                    d[i2 + 1][j1]--;
                    d[i2 + 1][j2 + 1]++;
                }
            }
        }

        // 3. 还原二维差分矩阵对应的计数矩阵（原地计算）
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                d[i + 1][j + 1] += d[i + 1][j] + d[i][j + 1] - d[i][j];
                if (grid[i][j] == 0 && d[i + 1][j + 1] == 0) {
                    return false;
                }
            }
        }
        return true;
    }
}