算法题总结
数组 1、如何处理循环数组 使用2倍的数组长度来取%完成一次循环,可以查找到前半部分的数组
1 2 3 4 5 6 7 for (int i=1 ;i<2 *nums.length;i++){ while (!st.isEmpty()&&nums[i]>nums[st.peek()]){ result[st.peek()] = nums[i % nums.length]; st.pop(); } st.push(i); }nums[i]=nums[i % nums.length];
2、二分查找 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 public int search (int [] nums, int target) { if (target < nums[0 ] || target > nums[nums.length - 1 ]) { return -1 ; } int left = 0 , right = nums.length - 1 ; while (left <= right) { int mid = left + ((right - left) >> 1 ); if (nums[mid] == target) return mid; else if (nums[mid] < target) left = mid + 1 ; else if (nums[mid] > target) right = mid - 1 ; } return -1 ; } int left = 0 , right = nums.length - 1 ; while (left <= right) { int mid = left + ((right - left) >> 1 ); else if (nums[mid] < target) left = mid + 1 ;[mid+1 ,right] else right = mid - 1 ;[left,mid-1 ] } return left; int left = 0 , right = nums.length; while (left < right) { int mid = left + ((right - left) >> 1 ); else if (nums[mid] < target) left = mid + 1 ;[mid+1 ,right) else right = mid ;[left,mid) } return left; int left = -1 , right = nums.length; while (left + 1 < right) { int mid = left + (right - left) / 2 ; if (nums[mid] < target) left = mid; else right = mid; } return right;
剑指 Offer 53 - I. 在排序数组中查找数字 I 考察二分法 考察了对于二分查找后对数据左右边界判断的方法
1 2 3 4 5 6 7 8 9 10 11 else { if (nums[begin] == nums[end]) { return end - begin + 1 ; } if (nums[begin] < target) { begin++; } if (nums[end] > target) { end--; } }
剑指 Offer 53 - II. 0~n-1中缺失的数字 思想依然是二分查找的方法 考察如何对于low和high两个数值的修改判断出缺失数字
1 2 3 4 5 int mid=low+(high-low)/2 ;if (nums[mid]!=mid)high=mid-1 ;else low=mid+1 ;return low;
思路是数量既然是1-n之中存在,但是却有n+1个笼子那可以只用二分查找缩小查找范围,如果小于mid数字多那就是小的那半重复,如果大于mid多就是大于部分重复
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 while (l<=r){ int half=(r-l)/2 +l; int count=0 ; for (int i = 0 ; i < nums.length; i++) { if (nums[i]<=half){ count++; } } if (count<=half){ l=half+1 ; } else { r=half-1 ; res=half; } }
这两个题目的破题关键:
定理一:只有在顺序区间内才可以通过区间两端的数值判断target是否在其中。
定理二:判断顺序区间还是乱序区间,只需要对比 left 和 right 是否是顺序对即可,left <= right,顺序区间,否则乱序区间。
定理三:每次二分都会至少存在一个顺序区间。
通过不断的用Mid二分,根据定理二,将整个数组划分成顺序区间和乱序区间,然后利用定理一判断target是否在顺序区间,如果在顺序区间,下次循环就直接取顺序区间,如果不在,那么下次循环就取乱序区间。
将数组一分为二,其中一定有一个是有序的,另一个可能是有序,也能是部分有序。 此时有序部分用二分法查找。无序部分再一分为二,其中一个一定有序,另一个可能有序,可能无序。就这样循环.
假设我们要找第 k 小数,我们可以每次循环排除掉 k/2 个数,所以我们采用递归的思路,为了防止数组长度小于 k/2,所以每次比较 min(k/2,len(数组) 对应的数字,把小的那个对应的数组的数字排除,将两个新数组进入递归,并且 k 要减去排除的数字的个数。递归出口就是当 k=1 或者其中一个数字长度是 0 了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 public double findMedianSortedArrays (int [] nums1, int [] nums2) { int n = nums1.length; int m = nums2.length; int left = (n + m + 1 ) / 2 ; int right = (n + m + 2 ) / 2 ; return (getKth(nums1,0 ,nums2,0 ,left)+ getKth(nums1,0 ,nums2,0 ,right)) * 0.5 ; } private int getKth (int [] nums1, int i, int [] nums2, int j, int k) { if ( i >= nums1.length) return nums2[j + k - 1 ]; if ( j >= nums2.length) return nums1[i + k - 1 ]; if (k == 1 ){ return Math.min(nums1[i], nums2[j]); } int midVal1 = (i + k / 2 - 1 < nums1.length) ? nums1[i + k / 2 - 1 ] : Integer.MAX_VALUE; int midVal2 = (j + k / 2 - 1 < nums2.length) ? nums2[j + k / 2 - 1 ] : Integer.MAX_VALUE; if (midVal1 < midVal2){ return getKth(nums1, i + k / 2 , nums2, j , k - k / 2 ); }else { return getKth(nums1, i, nums2, j + k / 2 , k - k / 2 ); } }
此题二分是因为本身矩阵是有序的,我们找值时总最小的最左值到最大的右下值进行二分查找,小于此值的都在上板部分,统计这部分个数,然后就可以返回结果,对于数组我们选用梯形遍历从左下角一直遍历到右上角
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 public int kthSmallest (int [][] matrix, int k) { int n = matrix.length; int left = matrix[0 ][0 ]; int right = matrix[n - 1 ][n - 1 ]; while (left < right) { int mid = left + ((right - left) >> 1 ); if (check(matrix, mid, k, n)) { right = mid; } else { left = mid + 1 ; } } return left; } public boolean check (int [][] matrix, int mid, int k, int n) { int i = n - 1 ; int j = 0 ; int num = 0 ; while (i >= 0 && j < n) { if (matrix[i][j] <= mid) { num += i + 1 ; j++; } else { i--; } } return num >= k; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 public int [] searchRange(int [] nums, int target) { int start = lowerBound(nums, target); if (start == nums.length || nums[start] != target) { return new int []{-1 , -1 }; } int end = lowerBound(nums, target + 1 ) - 1 ; return new int []{start, end}; } private int lowerBound (int [] nums, int target) { int left = 0 , right = nums.length - 1 ; while (left <= right) { int mid = left + (right - left) / 2 ; if (nums[mid] < target) { left = mid + 1 ; } else { right = mid - 1 ; } } return left; }
162. 寻找峰值
不难发现,如果 在确保有解的情况下,我们可以根据当前的分割点 mid 与左右元素的大小关系来指导 l 或者 r 的移动。
假设当前分割点 mid 满足关系 num[mid]>nums[mid+1] 的话,一个很简单的想法是 num[mid] 可能为峰值,而 nums[mid+1] 必然不为峰值,于是让 r=mid,从左半部分继续找峰值。
估计不少同学靠这个思路 AC 了,只能说做法对了,分析没对。
上述做法正确的前提有两个:
对于任意数组而言,一定存在峰值(一定有解);
1 2 3 4 5 6 7 8 9 10 public int findPeakElement (int [] nums) { int n = nums.length; int l = 0 , r = n - 1 ; while (l < r) { int mid = l + r >> 1 ; if (nums[mid] > nums[mid + 1 ]) r = mid; else l = mid + 1 ; } return r; }
3、删除数组时使用双指针法
双指针在遇到不满足条件时一起增加但是在满足条件时快指针动这样可以将后面元素加上来
1 2 3 4 5 6 7 8 9 10 11 public : int removeElement (vector<int >& nums, int val) int slowIndex = 0 ; for (int fastIndex = 0 ; fastIndex < nums.size (); fastIndex++) { if (val != nums[fastIndex]) { nums[slowIndex++] = nums[fastIndex]; } } return slowIndex; } };
双指针还可以用于前后倒序排列
1 2 3 4 5 6 7 8 9 10 11 12 13 14 public int [] sortedSquares(int [] nums) { int l = 0 ; int r = nums.length - 1 ; int [] res = new int [nums.length]; int j = nums.length - 1 ; while (l <= r){ if (nums[l] * nums[l] > nums[r] * nums[r]){ res[j--] = nums[l] * nums[l++]; }else { res[j--] = nums[r] * nums[r--]; } } return res; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public void sortColors (int [] nums) { int n = nums.length; int p0 = 0 , p1 = 0 ; for (int i = 0 ; i < n; ++i) { if (nums[i] == 1 ) { int temp = nums[i]; nums[i] = nums[p1]; nums[p1] = temp; ++p1; } else if (nums[i] == 0 ) { int temp = nums[i]; nums[i] = nums[p0]; nums[p0] = temp; if (p0 < p1) { temp = nums[i]; nums[i] = nums[p1]; nums[p1] = temp; } ++p0; ++p1; } } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 public int findUnsortedSubarray (int [] nums) { int n = nums.length; int l = 0 ; while (l + 1 < n && nums[l] <= nums[l + 1 ]) { l++; } if (l == n - 1 ) { return 0 ; } int r = n - 1 ; while (r - 1 >= 0 && nums[r] >= nums[r - 1 ]) { r--; } int min = nums[l]; int max = nums[r]; for (int i = l, j = r; i <= r && j >= l; i++, j--) { min = min < nums[i] ? min : nums[i]; max = max > nums[j] ? max : nums[j]; } while (l - 1 >= 0 && nums[l - 1 ] > min) { l--; } while (r + 1 < n && nums[r + 1 ] < max) { r++; } return r - l + 1 ; }
5、滑动窗口
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 int minSubArrayLen (int s, vector<int >& nums) int result = INT32_MAX; int sum = 0 ; int i = 0 ; int subLength = 0 ; for (int j = 0 ; j < nums.size (); j++) { sum += nums[j]; while (sum >= s) { subLength = (j - i + 1 ); result = result < subLength ? result : subLength; sum -= nums[i++]; } } return result == INT32_MAX ? 0 : result; }
注意需要统计次数时或者不求最大值时建议使用hashmap配合这样滑动窗口可以包含自身
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public String minWindow (String s, String t) { char [] sc = s.toCharArray();char [] tc = t.toCharArray(); int [] hash=new int [128 ]; for (char ch : tc) hash[ch]--; String res = "" ; int length=0 ; for (int i = 0 ,j=0 ; i < sc.length; i++) { hash[sc[i]]++; if (hash[sc[i]]<=0 )length++; while (length == tc.length && hash[sc[j]] > 0 ) hash[sc[j++]]--; if (length==tc.length) if (res.equals("" )||res.length()>i-j+1 ) res=s.substring(j,i+1 );` } return res; }
这两题拥有相同的思路将窗口开到指定大小在窗口大小内寻找是否符合要求,通过右指针到达具体窗口大小,左指针移动来整个平移滑动窗口,比较在规定窗口内的值是否符合答案.
1 2 #424 if (right - left + 1 > historyCharMax + k) {
1 2 #567 if (right-left+1 ==length1)return true ;
只要元素a>元素b而且元素a还在元素b的右侧,那么当滑动窗口移动时,元素b在不在队列里最大值都是元素a所以就可以在add时去除b元素,在弹出时判断该元素是否存在再弹出
1 2 3 4 5 6 7 8 9 10 11 12 13 int res[]=new int [nums.length-k+1 ];Deque<Integer>queue=new LinkedList <>(); for (int i = k,j=0 ; i <nums.length ; i++) { res[j++]=queue.peek(); if (nums[i-k]==queue.peek()) queue.poll(); while (!queue.isEmpty()&&queue.getLast()<nums[i]) { queue.removeLast(); } queue.offer(nums[i]); } return res;
我们每次移动一个单词的长度,也就是 3 个字符,这样所有的移动被分成了三类。总共需要移动对比的次数就是一个word的长度因为我们滑动窗口是以每个word长度进行的根据鸽笼原理大于word长度x开始的都是前面word长度以内开始的子情况,之后就是三种情况完全相同count == word_num 添加坐标,不同则清空left移动到不同的之后,对应word数量不同也清空left移动一位
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 public List<Integer> findSubstring (String s, String[] words) { List<Integer> res = new ArrayList <>(); if (s == null || s.length() == 0 || words == null || words.length == 0 ) return res; HashMap<String, Integer> map = new HashMap <>(); int one_word = words[0 ].length(); int word_num = words.length; int all_len = one_word * word_num; for (String word : words) { map.put(word, map.getOrDefault(word, 0 ) + 1 ); } for (int i = 0 ; i < one_word; i++) { int left = i, right = i, count = 0 ; HashMap<String, Integer> tmp_map = new HashMap <>(); while (right + one_word <= s.length()) { String w = s.substring(right, right + one_word); right += one_word; if (!map.containsKey(w)) { count = 0 ; left = right; tmp_map.clear(); } else { tmp_map.put(w, tmp_map.getOrDefault(w, 0 ) + 1 ); count++; while (tmp_map.getOrDefault(w, 0 ) > map.getOrDefault(w, 0 )) { String t_w = s.substring(left, left + one_word); count--; tmp_map.put(t_w, tmp_map.getOrDefault(t_w, 0 ) - 1 ); left += one_word; } if (count == word_num) res.add(left); } } } return res; }
排序 1、基本排序介绍
1.冒泡排序 (Bubble Sort)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public class BubbleSort1_01 { public static void main (String[] args) { int a[]={3 ,44 ,38 ,5 ,47 ,15 ,36 ,26 ,27 ,2 ,46 ,4 ,19 ,50 ,48 }; int count=0 ; for (int i = 0 ; i < a.length-1 ; i++) { boolean flag=true ; for (int j = 0 ; j < a.length-1 -i; j++) { if (a[j]>a[j+1 ]) { int temp=a[j]; a[j]=a[j+1 ]; a[j+1 ]=temp; flag=false ; } count++; } if (flag) { break ; } } System.out.println(Arrays.toString(a)); System.out.println("一共比较了:" +count+"次" ); } }
2.选择排序(Select Sort)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 3. import java.util.Arrays;public class SelectSort_02 { public static void main (String[] args) { int a[]={3 ,44 ,38 ,5 ,47 ,15 ,36 ,26 ,27 ,2 ,46 ,4 ,19 ,50 ,48 }; for (int i = 0 ; i < a.length-1 ; i++) { int index=i; for (int j = i+1 ; j < a.length; j++) { if (a[j]<a[index]) { index=j; } } int temp=a[index]; a[index]=a[i]; a[i]=temp; } System.out.println(Arrays.toString(a)); } }
3.插入排序(Insert Sort)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 import java.util.Arrays;public class InsertSort_03 { public static void main (String[] args) { int a[]={3 ,44 ,38 ,5 ,47 ,15 ,36 ,26 ,27 ,2 ,46 ,4 ,19 ,50 ,48 }; for (int i = 0 ; i < a.length; i++) { int insertValue=a[i]; int insertIndex=i-1 ; while (insertIndex>=0 && insertValue <a[insertIndex]) { a[insertIndex+1 ]=a[insertIndex]; insertIndex--; } a[insertIndex+1 ]=insertValue; } System.out.println(Arrays.toString(a)); } }
4.希尔排序(Shell Sort)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 import java.util.Arrays;public class ShellSort_04 { public static void main (String[] args) { int a[]={3 ,44 ,38 ,5 ,47 ,15 ,36 ,26 ,27 ,2 ,46 ,4 ,19 ,50 ,48 }; int count=0 ; for (int gap=a.length / 2 ; gap > 0 ; gap = gap / 2 ) { for (int i = gap; i < a.length; i++) { for (int j = i - gap; j>=0 ; j=j-gap) { if (a[j]>a[j+gap]) { int temp=a[j]; a[j]=a[j+gap]; a[j+gap]=temp; count++; } } } } System.out.println(count); System.out.println(Arrays.toString(a)); } }
5.快速排序(Quick Sort)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 import java.util.Arrays;public class QuickSort_05 { public static void main (String[] args) { int a[]={3 ,44 ,38 ,5 ,47 ,15 ,36 ,26 ,27 ,2 ,46 ,4 ,19 ,50 ,48 }; quicksort(a,0 ,a.length-1 ); System.out.println(Arrays.toString(a)); } private static void quicksort (int [] a, int low, int high) { int i,j; if (low>high) { return ; } i=low; j=high; int temp=a[low]; while (i<j){ while ( temp<=a[j] && i<j) { j--; } while ( temp>=a[i] && i<j) { i++; } if (i<j) { int t=a[i]; a[i]=a[j]; a[j]=t; } } a[low]=a[i]; a[i]=temp; quicksort(a, low, j-1 ); quicksort(a, j+1 , high); } }
6.归并排序(Merge Sort)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 import java.util.Arrays;public class MergeSort_06 { public static void main (String[] args) { int a[]={3 ,44 ,38 ,5 ,47 ,15 ,36 ,26 ,27 ,2 ,46 ,4 ,19 ,50 ,48 }; int temp[]=new int [a.length]; mergesort(a,0 ,a.length-1 ,temp); System.out.println(Arrays.toString(a)); } private static void mergesort (int [] a, int left, int right, int [] temp) { if (left<right) { int mid=(left+right)/2 ; mergesort(a, left, mid, temp); mergesort(a, mid+1 , right, temp); merge(a,left,right,mid,temp); } } private static void merge (int [] a, int left, int right, int mid, int [] temp) { int i=left; int j=mid+1 ; int t=0 ; while (i<=mid && j<=right) { if (a[i]<=a[j]) { temp[t]=a[i]; t++; i++; }else { temp[t]=a[j]; t++; j++; } } while (i<=mid) { temp[t]=a[i]; t++; i++; } while (j<=right) { temp[t]=a[j]; t++; j++; } t=0 ; int tempLeft=left; while (tempLeft<=right) { a[tempLeft]=temp[t]; t++; tempLeft++; } }
7.堆排序(Heap Sort) 第一步:构建初始堆buildHeap, 使用sink(arr,i, length)调整堆顶的值;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 public class Heap_Sort_07 { public static void main (String[] args) { int a[]={3 ,44 ,38 ,5 ,47 ,15 ,36 ,26 ,27 ,2 ,46 ,4 ,19 ,50 ,48 }; sort(a); System.out.println(Arrays.toString(a)); } public static void sort (int [] arr) { int length = arr.length; buildHeap(arr,length); for ( int i = length - 1 ; i > 0 ; i-- ) { int temp = arr[0 ]; arr[0 ] = arr[i]; arr[i] = temp; length--; sink(arr, 0 ,length); } } private static void buildHeap (int [] arr, int length) { for (int i = length / 2 ; i >= 0 ; i--) { sink(arr,i, length); } } private static void sink (int [] arr, int index, int length) { int leftChild = 2 * index + 1 ; int rightChild = 2 * index + 2 ; int present = index; if (leftChild < length && arr[leftChild] > arr[present]) { present = leftChild; } if (rightChild < length && arr[rightChild] > arr[present]) { present = rightChild; } if (present != index) { int temp = arr[index]; arr[index] = arr[present]; arr[present] = temp; sink(arr, present, length); } } }
8.计数排序 (Count Sort) 9.桶排序(Bucket Sort)
思路:
设置一个定量的数组当作空桶子。
寻访序列,并且把项目一个一个放到对应的桶子去。
对每个不是空的桶子进行排序。
从不是空的桶子里把项目再放回原来的序列中。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 public class BucketSort_09 { public static void sort (int [] arr) { int max = arr[0 ]; int min = arr[0 ]; int length = arr.length for (int i=1 ; i<length; i++) { if (arr[i] > max) { max = arr[i]; } else if (arr[i] < min) { min = arr[i]; } } int diff = max - min; ArrayList<ArrayList<Integer>> bucketList = new ArrayList <>(); for (int i = 0 ; i < length; i++){ bucketList.add(new ArrayList <>()); } float section = (float ) diff / (float ) (length - 1 ); for (int i = 0 ; i < length; i++){ int num = (int ) (arr[i] / section) - 1 ; if (num < 0 ){ num = 0 ; } bucketList.get(num).add(arr[i]); } for (int i = 0 ; i < bucketList.size(); i++){ Collections.sort(bucketList.get(i)); } int index = 0 ; for (ArrayList<Integer> arrayList : bucketList){ for (int value : arrayList){ arr[index] = value; index++; } } } }
10.基数排序(Raix Sort) 将问题转换为
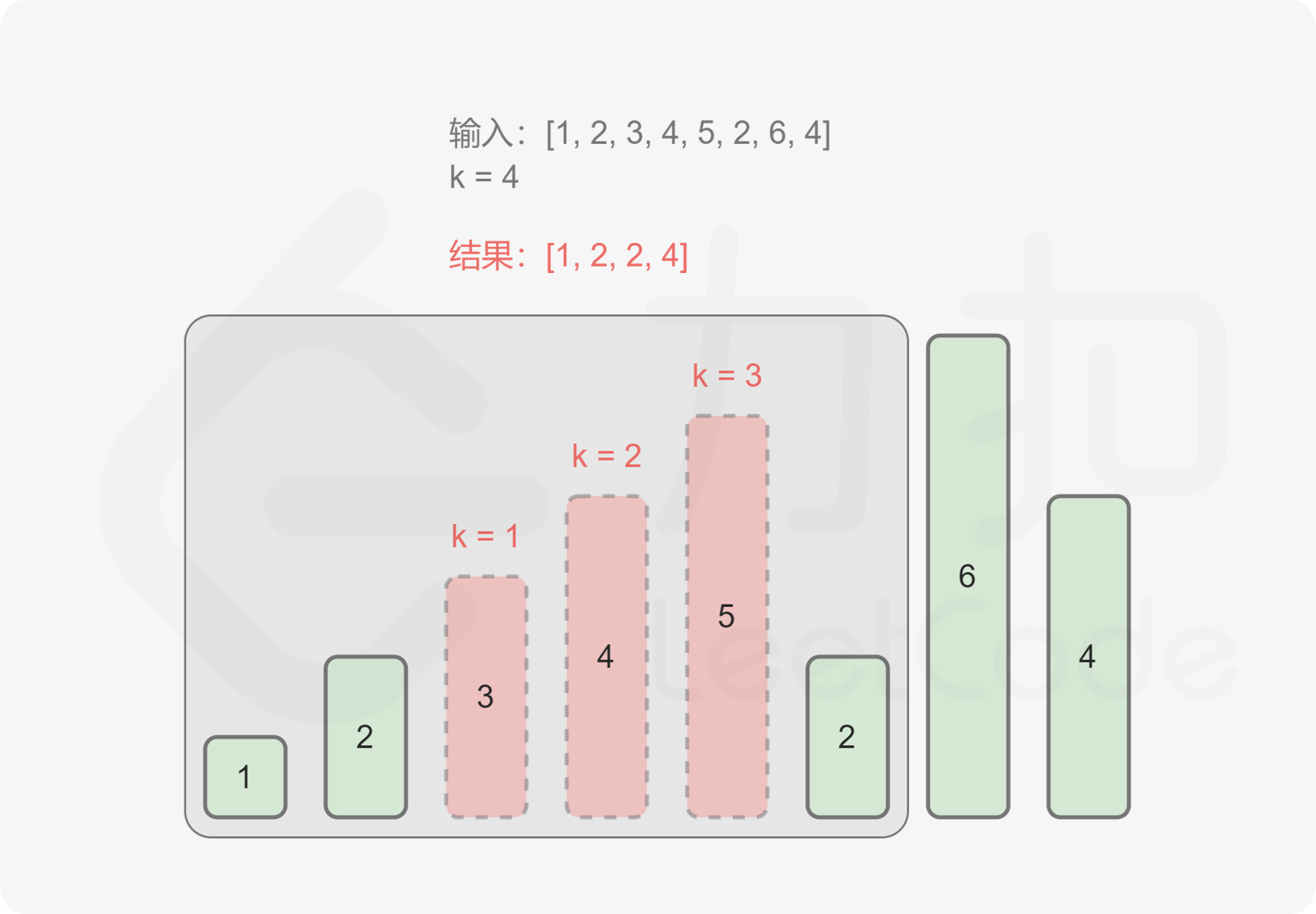
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public long kSum (int [] nums, int k) { int n = nums.length; long total = 0 ; for (int i = 0 ; i < n; i++) { if (nums[i] >= 0 ) { total += nums[i]; } else { nums[i] = -nums[i]; } } Arrays.sort(nums); long ret = 0 ; PriorityQueue<long []> pq = new PriorityQueue <long []>((a, b) -> Long.compare(a[0 ], b[0 ])); pq.offer(new long []{nums[0 ], 0 }); for (int j = 2 ; j <= k; j++) { long [] arr = pq.poll(); long t = arr[0 ]; int i = (int ) arr[1 ]; ret = t; if (i == n - 1 ) { continue ; } pq.offer(new long []{t + nums[i + 1 ], i + 1 }); pq.offer(new long []{t - nums[i] + nums[i + 1 ], i + 1 }); } return total - ret; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 class Solution {int count; public int reversePairs (int [] nums) { this .count = 0 ; merge(nums, 0 , nums.length - 1 ); return count; } public void merge (int [] nums, int left, int right) { int mid = left + ((right - left) >> 1 ); if (left < right) { merge(nums, left, mid); merge(nums, mid + 1 , right); mergeSort(nums, left, mid, right); } } public void mergeSort (int [] nums, int left, int mid, int right) { int [] temparr = new int [right - left + 1 ]; int index = 0 ; int temp1 = left, temp2 = mid + 1 ; while (temp1 <= mid && temp2 <= right) { if (nums[temp1] <= nums[temp2]) { temparr[index++] = nums[temp1++]; } else { count += (mid - temp1 + 1 ); temparr[index++] = nums[temp2++]; } } while (temp1 <= mid) { temparr[index++] = nums[temp1++]; } while (temp2 <= right) { temparr[index++] = nums[temp2++]; } for (int k = 0 ; k < temparr.length; k++) { nums[k + left] = temparr[k]; } } }
拓扑排序
选择图中一个入度为0的点,记录下来
在图中删除该点和所有以它为起点的边
重复1和2,直到图为空或没有入度为0的点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 public List<Integer> haveCircularDependency (int n, int [][] prerequisites) { List<List<Integer>> g = new ArrayList <>(); int [] indeg = new int [n]; List<Integer> res = new ArrayList <>(); for (int i = 0 ; i < n; i++) { g.add(new ArrayList <>()); } for (int [] prerequisite : prerequisites) { int a = prerequisite[0 ]; int b = prerequisite[1 ]; g.get(a).add(b); indeg[b]++; } Queue<Integer> q = new LinkedList <>(); for (int i = 0 ; i < n; i++) { if (indeg[i] == 0 ) { q.add(i); } } while (!q.isEmpty()) { int t = q.poll(); res.add(t); for (int j : g.get(t)) { indeg[j]--; if (indeg[j] == 0 ) { q.add(j); } } } if (res.size() == n) return res; else return new ArrayList <>(); }
链表 ps:在链表操作中不会直接使用head头节点操作而是使用一个新头指针来操作链表
1、206.反转链表
标准双指针问题
1 2 3 4 5 6 7 8 9 10 11 12 13 ListNode* reverseList (ListNode* head) { ListNode* temp; ListNode* cur = head; ListNode* pre = NULL ; while (cur) { temp = cur->next; cur->next = pre; pre = cur; cur = temp; } return pre; }
链表作题一定要画图,不画图,操作多个指针很容易乱,而且要操作的先后顺序
2、快慢指针法 3、环形链表判断
如果有环,如何找到这个环的入口 此时已经可以判断链表是否有环了,那么接下来要找这个环的入口了。
假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点 节点数为y。 从相遇节点 再到环形入口节点节点数为 z。 如图所示:
那么相遇时: slow指针走过的节点数为: x + y, fast指针走过的节点数:x + y + n (y + z),n为fast指针在环内走了n圈才遇到slow指针, (y+z)为 一圈内节点的个数A。
因为fast指针是一步走两个节点,slow指针一步走一个节点, 所以 fast指针走过的节点数 = slow指针走过的节点数 * 2:
1 (x + y) * 2 = x + y + n (y + z)
两边消掉一个(x+y): x + y = n (y + z)
因为要找环形的入口,那么要求的是x,因为x表示 头结点到 环形入口节点的的距离。
所以要求x ,将x单独放在左面:x = n (y + z) - y ,
再从n(y+z)中提出一个 (y+z)来,整理公式之后为如下公式:x = (n - 1) (y + z) + z 注意这里n一定是大于等于1的,因为 fast指针至少要多走一圈才能相遇slow指针。
这个公式说明什么呢?
先拿n为1的情况来举例,意味着fast指针在环形里转了一圈之后,就遇到了 slow指针了。
当 n为1的时候,公式就化解为 x = z,
这就意味着,从头结点出发一个指针,从相遇节点 也出发一个指针,这两个指针每次只走一个节点, 那么当这两个指针相遇的时候就是 环形入口的节点 。
同类型题目287. 寻找重复数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 while (fast != null && fast.next != null ) { slow = slow.next; fast = fast.next.next; if (slow == fast) { ListNode index1 = fast; ListNode index2 = head; while (index1 != index2) { index1 = index1.next; index2 = index2.next; } return index1; } }
19. 删除链表的倒数第 N 个结点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public ListNode removeNthFromEnd (ListNode head, int n) { ListNode dummyNode = new ListNode (0 ); dummyNode.next = head; ListNode fast=dummyNode; ListNode slow=dummyNode; for (int i = 0 ; i < n ; i++){ fast = fast.next; } while (fast.next != null ){ fast = fast.next; slow = slow.next; } slow.next = slow.next.next; return dummyNode.next; }
160. 相交链表
循环遍历直到相交
1 2 3 4 5 6 7 8 public ListNode getIntersectionNode (ListNode headA, ListNode headB) { ListNode A = headA, B = headB; while (A != B) { A = A != null ? A.next : headB; B = B != null ? B.next : headA; } return A; }
4、分割链表反转
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 public class ReorderList { public void reorderList (ListNode head) { ListNode fast = head, slow = head; while (fast.next != null && fast.next.next != null ) { slow = slow.next; fast = fast.next.next; } ListNode right = slow.next; slow.next = null ; right = reverseList(right); ListNode left = head; while (right != null ) { ListNode curLeft = left.next; left.next = right; left = curLeft; ListNode curRight = right.next; right.next = left; right = curRight; } } public ListNode reverseList (ListNode head) { ListNode headNode = new ListNode (0 ); ListNode cur = head; ListNode next = null ; while (cur != null ) { next = cur.next; cur.next = headNode.next; headNode.next = cur; cur = next; } return headNode.next; } }
使用虚拟构造一个头节点pre来完成对于一个新链表的创建 例如合并两个排序链表时就可以使用这个方法来创建一个新链表 1 2 3 4 5 6 ListNode pre = new ListNode (0 ); ListNode cur = pre; return pre.next;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public ListNode mergeTwoLists (ListNode l1, ListNode l2) { ListNode cur=new ListNode (0 ); ListNode re=cur; while (l1!=null &&l2!=null ){ if (l1.val<l2.val){ re.next=l1; l1=l1.next; } else { re.next=l2; l2=l2.next; } re=re.next; } if (l1==null ){ re.next=l2; }else re.next=l1; return cur.next; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 public ListNode insertionSortList (ListNode head) { if (head==null )return head; ListNode temp=new ListNode (0 ); temp.next=head; ListNode sorted=head,cur=head.next; while (cur!=null ){ if (sorted.val<=cur.val){ sorted=sorted.next; } else { ListNode pre=temp; while (pre.next.val<=cur.val){ pre=pre.next; } sorted.next=cur.next; cur.next=pre.next; pre.next=cur; } cur=sorted.next; } return temp.next; } public ListNode sortList (ListNode head) { if (head == null || head.next == null ) return head; ListNode slow=head,fast=head.next; while (fast!=null &&fast.next!=null ){ slow=slow.next; fast=fast.next.next; } ListNode temp=slow.next; slow.next=null ; ListNode left=sortList(head); ListNode right=sortList(temp); ListNode node = merge(left,right); return node; } public ListNode merge (ListNode left,ListNode right) { ListNode res=new ListNode (0 ); ListNode temp=res,temp1=left,temp2=right; while (temp1!=null &&temp2!=null ){ if (temp1.val> temp2.val){ temp.next=temp2; temp2=temp2.next; temp=temp.next; } else { temp.next=temp1; temp1=temp1.next; temp=temp.next; } } if (temp1==null )temp.next=temp2; else temp.next=temp1; return res.next; }
5、合并k个链表 这题就是更新于合并两个排序链表
将k个链表两两合并即可完成
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 public ListNode mergeKLists (ListNode[] lists) { if (lists == null || lists.length == 0 ) return null ; return merge(lists, 0 , lists.length - 1 ); } private ListNode merge (ListNode[] lists, int left, int right) { if (left == right) return lists[left]; int mid = left + (right - left) / 2 ; ListNode l1 = merge(lists, left, mid); ListNode l2 = merge(lists, mid + 1 , right); return mergeTwoLists(l1, l2); } private ListNode mergeTwoLists (ListNode l1, ListNode l2) { if (l1 == null ) return l2; if (l2 == null ) return l1; if (l1.val < l2.val) { l1.next = mergeTwoLists(l1.next, l2); return l1; } else { l2.next = mergeTwoLists(l1,l2.next); return l2; } }
小tips:使用while 加||可以在内部在判断l1或者l2是否为空这样可以哪怕一边为空都可以继续循环
1 2 3 4 while (l1!=null ||l2!=null ){ int num1 = l1 == null ? 0 : l1.val; int num2 = l2 == null ? 0 : l2.val;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public ListNode addTwoNumbers (ListNode l1, ListNode l2) { ListNode pre=new ListNode (0 ); ListNode cur=pre; int carry=0 ; while (l1!=null ||l2!=null ){ int num1 = l1 == null ? 0 : l1.val; int num2 = l2 == null ? 0 : l2.val; int sum=num1+num2+carry; carry=sum/10 ; int val=sum%10 ; cur.next = new ListNode (val); cur=cur.next; if (l1!=null )l1=l1.next; if (l2!=null )l2=l2.next; } if (carry == 1 ) { cur.next = new ListNode (carry); } return pre.next; }
实现关键就在于将其分组拆分后先反转链表再拼接
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public ListNode reverseKGroup (ListNode head, int k) { ListNode hair = new ListNode (0 ); hair.next = head; ListNode pre = hair; ListNode end=hair; while (end.next != null ) { for (int i = 0 ; i < k&& end != null ; i++) { end=end.next; } if (end==null )break ; ListNode next=end.next; ListNode start=pre.next; end.next=null ; pre.next=reverse(start); start.next=next; end=start; pre=start; } return hair.next; }
记录pre指针位置,最后链接时pre的next链接right pre.next.next链接succ就可以
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public ListNode reverseBetween (ListNode head, int left, int right) { ListNode dummy = new ListNode (0 , head), p0 = dummy; for (int i = 0 ; i < left - 1 ; ++i) p0 = p0.next; ListNode pre = null , cur = p0.next; for (int i = 0 ; i < right - left + 1 ; ++i) { ListNode nxt = cur.next; cur.next = pre; pre = cur; cur = nxt; } p0.next.next = cur; p0.next = pre; return dummy.next; }
关键点在与将链表链接成环,先链接再斩断
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public ListNode rotateRight (ListNode head, int k) { if (k == 0 || head == null || head.next == null ) { return head; } int n = 1 ; ListNode iter = head; while (iter.next != null ) { iter = iter.next; n++; } int add = n - k % n; if (add == n) { return head; } iter.next = head; while (add-- > 0 ) { iter = iter.next; } ListNode ret = iter.next; iter.next = null ; return ret; }
给定一个奇数位升序,偶数位降序的链表,将其重新排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 class ListNode { int val; ListNode next; ListNode(int x) { val = x; next = null ; } } class Solution { public ListNode sortOddEvenList (ListNode head) { if (head == null || head.next == null ) { return head; } ListNode[] partitions = partition(head); ListNode oddList = partitions[0 ]; ListNode evenList = reverse(partitions[1 ]); return merge(oddList, evenList); } private ListNode[] partition(ListNode head) { ListNode evenHead = head.next; ListNode odd = head, even = evenHead; while (even != null && even.next != null ) { odd.next = even.next; odd = odd.next; even.next = odd.next; even = even.next; } odd.next = null ; return new ListNode []{head, evenHead}; } private ListNode reverse (ListNode head) { ListNode dummy = new ListNode (-1 ); ListNode p = head; while (p != null ) { ListNode temp = p.next; p.next = dummy.next; dummy.next = p; p = temp; } return dummy.next; } private ListNode merge (ListNode p, ListNode q) { ListNode dummy = new ListNode (-1 ); ListNode r = dummy; while (p != null && q != null ) { if (p.val <= q.val) { r.next = p; p = p.next; } else { r.next = q; q = q.next; } r = r.next; } if (p != null ) { r.next = p; } if (q != null ) { r.next = q; } return dummy.next; } }
哈希 哈希map遍历 1、 通过ForEach循环进行遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 public class Test { public static void main (String[] args) throws IOException { Map<Integer, Integer> map = new HashMap <Integer, Integer>(); map.put(1 , 10 ); map.put(2 , 20 ); for (Map.Entry<Integer, Integer> entry : map.entrySet()) { System.out.println("Key = " + entry.getKey() + ", Value = " + entry.getValue()); } } }
2、 ForEach迭代键值对方式
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public class Test { public static void main (String[] args) throws IOException { Map<Integer, Integer> map = new HashMap <Integer, Integer>(); map.put(1 , 10 ); map.put(2 , 20 ); for (Integer key : map.keySet()) { System.out.println("Key = " + key); } for (Integer value : map.values()) { System.out.println("Value = " + value); } } }
3、使用带泛型的迭代器进行遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 public class Test { public static void main (String[] args) throws IOException { Map<Integer, Integer> map = new HashMap <Integer, Integer>(); map.put(1 , 10 ); map.put(2 , 20 ); Iterator<Map.Entry<Integer, Integer>> entries = map.entrySet().iterator(); while (entries.hasNext()) { Map.Entry<Integer, Integer> entry = entries.next(); System.out.println("Key = " + entry.getKey() + ", Value = " + entry.getValue()); } } }
4、使用不带泛型的迭代器进行遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public class Test { public static void main (String[] args) throws IOException { Map map = new HashMap (); map.put(1 , 10 ); map.put(2 , 20 ); Iterator<Map.Entry> entries = map.entrySet().iterator(); while (entries.hasNext()) { Map.Entry entry = (Map.Entry) entries.next(); Integer key = (Integer) entry.getKey(); Integer value = (Integer) entry.getValue(); System.out.println("Key = " + key + ", Value = " + value); } } }
5、通过Java8 Lambda表达式遍历
1 2 3 4 5 6 7 8 public class Test { public static void main (String[] args) throws IOException { Map<Integer, Integer> map = new HashMap <Integer, Integer>(); map.put(1 , 10 ); map.put(2 , 20 ); map.forEach((k, v) -> System.out.println("key: " + k + " value:" + v)); } }
computeIfAbsent()方法 hashMap.computeIfAbsent(“china”, key -> getValues(key)).add(“liSi”);的意思表示key为“China”的建值对是否存在,返回的是value的值。
如果存在则获取china的值,并操作值的set添加数据“lisi”。
如果不存在,则调用方法,新创建set结构,将”lisi”添加到set中,再存入到hashMap中
破题关键在于第一破除环形数组,在正常数组背后加头元素成为链式数组 ,第二找到两个相同的元素离得最远的距离除以二就是就是传播所需要的长时间
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public int minimumSeconds (List<Integer> nums) { int size = nums.size(); Map<Integer,List<Integer>>map =new HashMap <>(); for (int i = 0 ; i <size ; i++) { map.computeIfAbsent(nums.get(i), k -> new ArrayList <>()).add(i); } int res=size; for (List<Integer> a : map.values()) { a.add(a.get(0 ) + size); int mx = 0 ; for (int i = 1 ; i < a.size(); ++i) { mx = Math.max(mx, (a.get(i) - a.get(i - 1 )) / 2 ); } res = Math.min(res, mx); } return res; }
1、基本哈希映射 2、字母相同哈希思路 开一个int hash[26]进行哈希映射,之后选择取min来完成相同字母的统计
3、多数之和
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public int [] twoSum(int [] nums, int target) { int [] res = new int [2 ]; if (nums == null || nums.length == 0 ){ return res; } Map<Integer, Integer> map = new HashMap <>(); for (int i = 0 ; i < nums.length; i++){ int temp = target - nums[i]; if (map.containsKey(temp)){ res[1 ] = i; res[0 ] = map.get(temp); break ; } map.put(nums[i], i); } return res; }
四数相加同理将两个数分组然后使用哈希匹配
4、s三数之和以上不适合用哈希 使用双指针法完成 给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
对数组先进行升序排序
依然还是在数组中找到 abc 使得a + b +c =0,我们这里相当于 a = nums[i],b = nums[left],c = nums[right]。
接下来如何移动left 和right呢, 如果nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了,因为数组是排序后了,所以right下标就应该向左移动,这样才能让三数之和小一些。
如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了,left 就向右移动,才能让三数之和大一些,直到left与right相遇为止。
5、hashset去重 128. 最长连续序列
从小的开始去找大的跳过大的数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public int longestConsecutive (int [] nums) { Set<Integer> num_set = new HashSet <Integer>(); for (int num : nums) { num_set.add(num); } int longestStreak = 0 ; for (int num : num_set) { if (!num_set.contains(num - 1 )) { int currentNum = num; int currentStreak = 1 ; while (num_set.contains(currentNum + 1 )) { currentNum += 1 ; currentStreak += 1 ; } longestStreak = Math.max(longestStreak, currentStreak); } } return longestStreak; }
纯模拟题
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 private Map<Integer, Tweet> twitter;private Map<Integer, Set<Integer>> followings;private static int timestamp = 0 ;private static PriorityQueue<Tweet> maxHeap;public Twitter () { followings = new HashMap <>(); twitter = new HashMap <>(); maxHeap = new PriorityQueue <>((o1, o2) -> -o1.timestamp + o2.timestamp); } public void postTweet (int userId, int tweetId) { timestamp++; if (twitter.containsKey(userId)) { Tweet oldHead = twitter.get(userId); Tweet newHead = new Tweet (tweetId, timestamp); newHead.next = oldHead; twitter.put(userId, newHead); } else { twitter.put(userId, new Tweet (tweetId, timestamp)); } } public List<Integer> getNewsFeed (int userId) { maxHeap.clear(); if (twitter.containsKey(userId)) { maxHeap.offer(twitter.get(userId)); } Set<Integer> followingList = followings.get(userId); if (followingList != null && followingList.size() > 0 ) { for (Integer followingId : followingList) { Tweet tweet = twitter.get(followingId); if (tweet != null ) { maxHeap.offer(tweet); } } } List<Integer> res = new ArrayList <>(10 ); int count = 0 ; while (!maxHeap.isEmpty() && count < 10 ) { Tweet head = maxHeap.poll(); res.add(head.id); if (head.next != null ) { maxHeap.offer(head.next); } count++; } return res; } public void follow (int followerId, int followeeId) { if (followeeId == followerId) { return ; } Set<Integer> followingList = followings.get(followerId); if (followingList==null ){ Set<Integer> init = new HashSet <>(); init.add(followeeId); followings.put(followerId, init); } else { if (followingList.contains(followeeId)) { return ; } followingList.add(followeeId); } } public void unfollow (int followerId, int followeeId) { if (followeeId==followerId)return ; Set<Integer>followinglist=followings.get(followerId); if (followinglist==null )return ; followinglist.remove(followeeId); } private class Tweet { private int id; private int timestamp; private Tweet next; public Tweet (int id, int timestamp) { this .id = id; this .timestamp = timestamp; } }
两数异或 421. 数组中两个数的最大异或值
以上两题是类似于两数之和的两数异或判断
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 public int findMaximumXOR (int [] nums) { int max = 0 ; for (int x : nums) { max = Math.max(max, x); } int highBit = 31 - Integer.numberOfLeadingZeros(max); int ans = 0 , mask = 0 ; Set<Integer> seen = new HashSet <>(); for (int i = highBit; i >= 0 ; i--) { seen.clear(); mask |= 1 << i; int newAns = ans | (1 << i); for (int x : nums) { x &= mask; if (seen.contains(newAns ^ x)) { ans = newAns; break ; } seen.add(x); } } return ans; } public int maximumStrongPairXor (int [] nums) { Arrays.sort(nums); int highBit = 31 - Integer.numberOfLeadingZeros(nums[nums.length - 1 ]); int ans = 0 , mask = 0 ; Map<Integer, Integer> mp = new HashMap <>(); for (int i = highBit; i >= 0 ; i--) { mp.clear(); mask |= 1 << i; int newAns = ans | (1 << i); for (int y : nums) { int maskY = y & mask; if (mp.containsKey(newAns ^ maskY) && mp.get(newAns ^ maskY) * 2 >= y) { ans = newAns; break ; } mp.put(maskY, y); } } return ans; }
这题需要找到这个计算规律将寻找字符频数转换为区间内次数计算
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public int uniqueLetterString (String s) { Map<Character, List<Integer>> map = new HashMap (); char [] sc = s.toCharArray(); for (int i = 0 ; i < sc.length; i++) { if (!map.containsKey(sc[i])) map.put(sc[i], new ArrayList ()); map.get(sc[i]).add(i); } int result = 0 ; for (Map.Entry<Character, List<Integer>> entry : map.entrySet()) { int head = -1 , tail = -1 ; List<Integer> item = entry.getValue(); for (int i = 0 ; i < item.size(); i++) { tail = (i < item.size() - 1 ) ? item.get(i + 1 ) : sc.length; result += (item.get(i) - head) * (tail - item.get(i)); head = item.get(i); } } return result; }
442. 数组中重复的数据
原地hash 448 41 题也是一样的
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public List<Integer> findDuplicates (int [] nums) { for (int i=0 ;i<nums.length;i++){ while (nums[i]!=nums[nums[i]-1 ]){ swap(nums,i,nums[i]-1 ); } } List<Integer> ans = new ArrayList <Integer>(); for (int i = 0 ; i < nums.length; ++i) { if (nums[i] - 1 != i) { ans.add(nums[i]); } } return ans; } public void swap (int [] nums, int index1, int index2) { int temp = nums[index1]; nums[index1] = nums[index2]; nums[index2] = temp; }
由字符串预处理得到这样的哈希数组和次方数组复杂度为 O(n)。当我们需要计算子串 s[i…j] 的哈希值,只需要利用前缀和思想 h[j]−h[i−1]∗p[j−i+1] 即可在 O(1) 时间内得出哈希值(与子串长度无关)。类似于前缀和你需要求i到j的哈希值时就用 h[j]−h[i−1]∗p[j−i+1] 得到然后每次比较两个串的值是否相同
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution {int N = (int )1e5 +10 , P = 131313 ; int [] h = new int [N], p = new int [N]; public List<String> findRepeatedDnaSequences (String s) { int n = s.length(); List<String> ans = new ArrayList <>(); p[0 ] = 1 ; for (int i = 1 ; i <= n; i++) { h[i] = h[i - 1 ] * P + s.charAt(i - 1 ); p[i] = p[i - 1 ] * P; } Map<Integer, Integer> map = new HashMap <>(); for (int i = 1 ; i + 10 - 1 <= n; i++) { int j = i + 10 - 1 ; int hash = h[j] - h[i - 1 ] * p[j - i + 1 ]; int cnt = map.getOrDefault(hash, 0 ); if (cnt == 1 ) ans.add(s.substring(i - 1 , i + 10 - 1 )); map.put(hash, cnt + 1 ); } return ans; } }
1044. 最长重复子串
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class Solution { long [] h, p; public String longestDupSubstring (String s) { int P = 1313131 , n = s.length(); h = new long [n + 10 ]; p = new long [n + 10 ]; p[0 ] = 1 ; for (int i = 0 ; i < n; i++) { p[i + 1 ] = p[i] * P; h[i + 1 ] = h[i] * P + s.charAt(i); } String ans = "" ; int l = 0 , r = n; while (l < r) { int mid = l + r + 1 >> 1 ; String t = check(s, mid); if (t.length() != 0 ) l = mid; else r = mid - 1 ; ans = t.length() > ans.length() ? t : ans; } return ans; } String check (String s, int len) { int n = s.length(); Set<Long> set = new HashSet <>(); for (int i = 1 ; i + len - 1 <= n; i++) { int j = i + len - 1 ; long cur = h[j] - h[i - 1 ] * p[j - i + 1 ]; if (set.contains(cur)) return s.substring(i - 1 , j); set.add(cur); } return "" ; } }
字符串 1.方法1:char[]数组转成String,使用 String 类的 valueOf() 方法 我们可以使用 String 类的 String.valueOf(char) 方法和 Character 类的 Character.toString(char) 方法在 java 中将 char 转换为 String。
String.valueOf(char) 方法和 Character 类的 Character.toString(char)方法的区别: 1.String.valueOf(char) 方法可以将char[] 和char 变量名转成String类型 2.Character.toString(char)方法只能在char 变量名转成String类型 2、字符翻转 本质就是双指针对于前面字符交换
在遇到交换k位之后的字符时,思路为翻转后k个再翻转前k个最后翻转整个字符
3、kmp算法 (1)KMP的主要思想是当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头再去做匹配了。 (2)所以如何记录已经匹配的文本内容,是KMP的重点,也是next数组肩负的重任。 前缀表是用来回退的,它记录了模式串与主串(文本串)不匹配的时候,模式串应该从哪里开始重新匹配。
(3)如何计算前缀表 接下来就要说一说怎么计算前缀表。
如图:
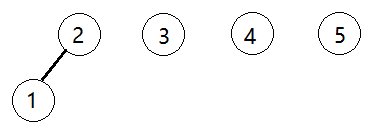
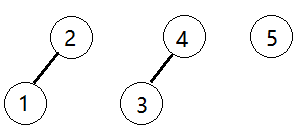
长度为前1个字符的子串a,最长相同前后缀的长度为0。(注意字符串的前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串 ;后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串 。)
长度为前2个字符的子串aa,最长相同前后缀的长度为1。
长度为前3个字符的子串aab,最长相同前后缀的长度为0。
以此类推: 长度为前4个字符的子串aaba,最长相同前后缀的长度为1。 长度为前5个字符的子串aabaa,最长相同前后缀的长度为2。 长度为前6个字符的子串aabaaf,最长相同前后缀的长度为0。
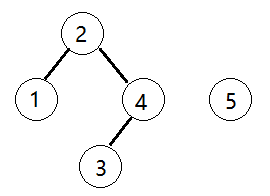
那么把求得的最长相同前后缀的长度就是对应前缀表的元素,如图:
可以看出模式串与前缀表对应位置的数字表示的就是:下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。
再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如动画所示:
找到的不匹配的位置, 那么此时我们要看它的前一个字符的前缀表的数值是多少。
为什么要前一个字符的前缀表的数值呢,因为要找前面字符串的最长相同的前缀和后缀。
所以要看前一位的 前缀表的数值。
前一个字符的前缀表的数值是2, 所以把下标移动到下标2的位置继续比配。 可以再反复看一下上面的动画。
最后就在文本串中找到了和模式串匹配的子串了。
其实这并不涉及到KMP的原理,而是具体实现,next数组既可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 public void getNext (int [] next, String s) { int j = -1 ; next[0 ] = j; for (int i = 1 ; i < s.length(); i++){ while (j >= 0 && s.charAt(i) != s.charAt(j+1 )){ j=next[j]; } if (s.charAt(i) == s.charAt(j+1 )){ j++; } next[i] = j; } } public int strStr (String haystack, String needle) { if (needle.length()==0 ){ return 0 ; } int [] next = new int [needle.length()]; getNext(next, needle); int j = -1 ; for (int i = 0 ; i < haystack.length(); i++){ while (j>=0 && haystack.charAt(i) != needle.charAt(j+1 )){ j = next[j]; } if (haystack.charAt(i) == needle.charAt(j+1 )){ j++; } if (j == needle.length()-1 ){ return (i-needle.length()+1 ); } } return -1 ; }
操作等价于把末尾字母一个一个地移到开头,比如字符串 abcd,「把 cd 移到开头」和「先把 d 移到开头,再把 c 移到开头」,都会得到字符串 cdab。
所以操作得到的是 sss 的循环同构字符串,这意味着,只要 s+s中包含 t,就可以从 sss 变成 t。比如示例 1 的 s+s=abcdabcd,其中就包含一个 cdab。
计算有多少个 sss 的循环同构字符串等于 t,记作 ccc。这可以用 KMP 等字符串匹配算法解决,即寻找 ttt 在 s+ss+ss+s(去掉最后一个字符)中的出现次数。例如示例 2 中 c=3。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 public int numberOfWays (String s, String t, long k) { int n = s.length(); int c = kmpSearch(s + s.substring(0 , n - 1 ), t); long [][] m = { {c - 1 , c}, {n - c, n - 1 - c}, }; m = pow(m, k); return s.equals(t) ? (int ) m[0 ][0 ] : (int ) m[0 ][1 ]; } private int [] calcMaxMatch(String s) { int [] match = new int [s.length()]; int c = 0 ; for (int i = 1 ; i < s.length(); i++) { char v = s.charAt(i); while (c > 0 && s.charAt(c) != v) { c = match[c - 1 ]; } if (s.charAt(c) == v) { c++; } match[i] = c; } return match; } private int kmpSearch (String text, String pattern) { int [] match = calcMaxMatch(pattern); int lenP = pattern.length(); int matchCnt = 0 ; int c = 0 ; for (int i = 0 ; i < text.length(); i++) { char v = text.charAt(i); while (c > 0 && pattern.charAt(c) != v) { c = match[c - 1 ]; } if (pattern.charAt(c) == v) { c++; } if (c == lenP) { matchCnt++; c = match[c - 1 ]; } } return matchCnt; } private static final long MOD = (long ) 1e9 + 7 ;private long [][] multiply(long [][] a, long [][] b) { long [][] c = new long [2 ][2 ]; for (int i = 0 ; i < 2 ; i++) { for (int j = 0 ; j < 2 ; j++) { c[i][j] = (a[i][0 ] * b[0 ][j] + a[i][1 ] * b[1 ][j]) % MOD; } } return c; } private long [][] pow(long [][] a, long n) { long [][] res = {{1 , 0 }, {0 , 1 }}; for (; n > 0 ; n /= 2 ) { if (n % 2 > 0 ) { res = multiply(res, a); } a = multiply(a, a); } return res; }
4.Z 函数(扩展 KMP) 对于个长度为 n 的字符串s。定义函数 **z[i]**表示 s 和 **s[i,n-1]**(即以 s[i]开头的后缀)的最长公共前缀(LCP)的长度。z被称为 s 的 Z 函数 。特别地, z[0] = 0
Z Algorithm (JavaScript Demo) (utdallas.edu)
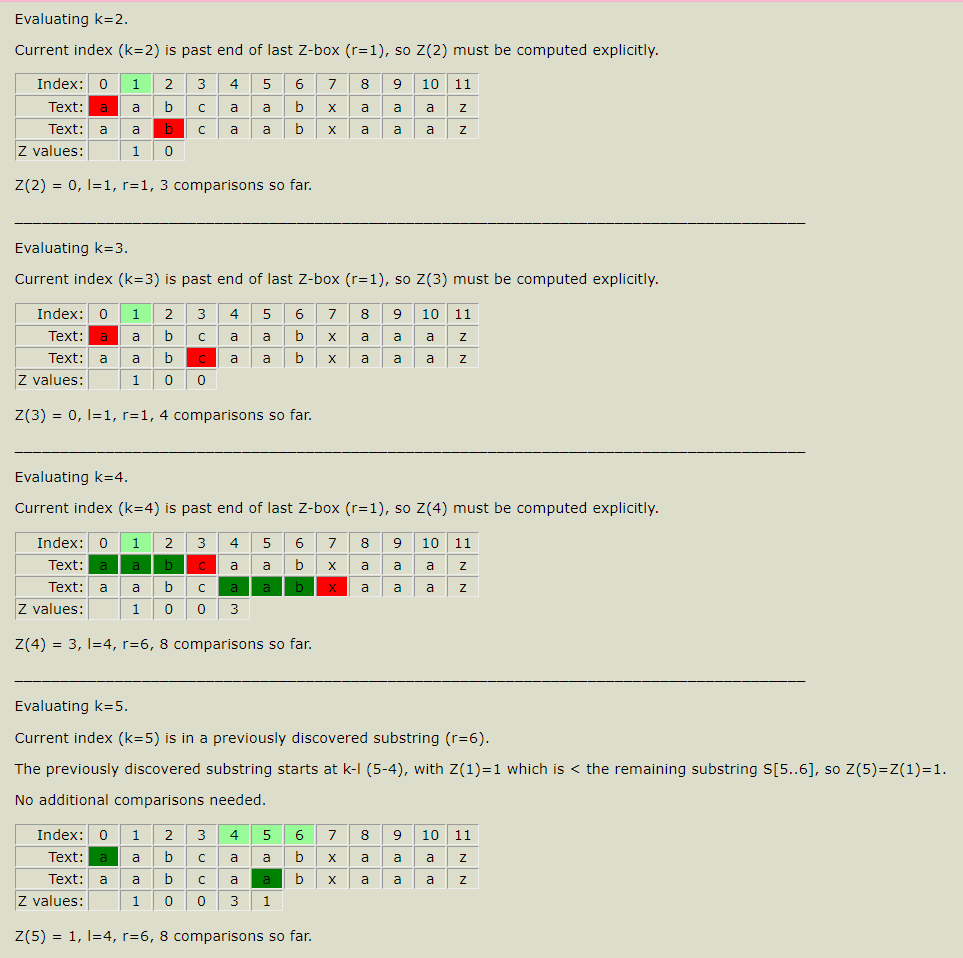
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public int minimumTimeToInitialState (String S, int k) { char [] s = S.toCharArray(); int n = s.length; int [] z = new int [n]; int l = 0 , r = 0 ; for (int i = 1 ; i < n; i++) { if (i <= r) { z[i] = Math.min(z[i - l], r - i + 1 ); } while (i + z[i] < n && s[z[i]] == s[i + z[i]]) { l = i; r = i + z[i]; z[i]++; } if (i % k == 0 && z[i] >= n - i) { return i / k; } } return (n - 1 ) / k + 1 ; }
5、状态机
此题有个记录字符串字符出现频率的方法
1 masks[i] |= 1 << (word.charAt(j) - 'a' );
对于字符 ‘a’:1 << (word.charAt(j) - 'a') 计算为 1 << 0,结果是 1(二进制:0000 0001)。
对于字符 ‘b’:1 << (word.charAt(j) - 'a') 计算为 1 << 1,结果是 2(二进制:0000 0010)。
对于字符 ‘c’:1 << (word.charAt(j) - 'a') 计算为 1 << 2,结果是 4(二进制:0000 0100)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public int maxProduct (String[] words) { int length = words.length; int [] masks = new int [length]; for (int i = 0 ; i < length; i++) { String word = words[i]; int wordLength = word.length(); for (int j = 0 ; j < wordLength; j++) { masks[i] |= 1 << (word.charAt(j) - 'a' ); } } int maxProd = 0 ; for (int i = 0 ; i < length; i++) { for (int j = i + 1 ; j < length; j++) { if ((masks[i] & masks[j]) == 0 ) { maxProd = Math.max(maxProd, words[i].length() * words[j].length()); } } } return maxProd; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public int maximumSwap (int num) { char [] chars = String.valueOf(num).toCharArray(); int maxIdx = chars.length - 1 ; int low=-1 ,high=0 ; for (int i = chars.length-2 ; i >=0 ;i--) { if (chars[i]>chars[maxIdx]) { maxIdx=i; } else if (chars[i] < chars[maxIdx]){ low=i; high= maxIdx; } } if (low == -1 ) { return num; } char s=chars[low]; chars[low]=chars[high]; chars[high]=s; return Integer.parseInt(String.valueOf(chars)); }
栈与队列 Stack add & push
共同点:
add,push都可以向stack中添加元素。
不同点:
add是继承自Vector的方法,且返回值类型是boolean。
push是Stack自身的方法,返回值类型是参数类类型。
具体的看源码:
1 2 3 4 5 6 public synchronized boolean add (E e) { modCount++; ensureCapacityHelper(elementCount + 1 ); elementData[elementCount++] = e; return true ; }
1 2 3 4 5 public E push (E item) { addElement(item); return item; }
peek & pop
共同点:
peek,pop都是返回栈顶元素。
不同点:
peek()函数返回栈顶的元素,但不弹出该栈顶元素。
150. 逆波兰表达式求值
此题关键在于栈存放数字在遍历到符号时取出数字运算即可
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Stack<Integer>caculate=new Stack <>(); for (int i = 0 ;i<tokens.length;i++){ if ("+" .equals(tokens[i])) { caculate.push(caculate.pop() + caculate.pop()); } else if ("-" .equals(tokens[i])) { caculate.push(-caculate.pop() + caculate.pop()); } else if ("*" .equals(tokens[i])) { caculate.push(caculate.pop() * caculate.pop()); } else if ("/" .equals(tokens[i])) { int temp1 = caculate.pop(); int temp2 = caculate.pop(); caculate.push(temp2 / temp1); } else { caculate.push(Integer.valueOf(tokens[i])); } } return caculate.pop();
739. 每日温度
此题在于使用stack存储数组下标这样在栈中取出时自然可以定位第几天的前面的最高温是多少
1 2 3 4 while (!stack.isEmpty()&&temperatures[i]>temperatures[stack.peek()]){ res[stack.peek()]=i-stack.peek(); stack.pop(); }
853. 车队
抓住一个思想,如果你位置在我前面,最终到达时间比我慢我们两个之间就会相遇,即使两个车相遇但是以最慢的那个车速度来行驶,行驶时间都是最慢那个车的最长时间,所以继续用那个车的最长时间来进行比较看是否会有二次相遇.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public int carFleet (int target, int [] position, int [] speed) { Map<Integer,Integer>map=new TreeMap <>(); for (int i = 0 ; i < position.length; i++) { map.put(position[i],speed[i]); } Stack<Float>stack = new Stack <>(); for (Map.Entry<Integer, Integer> entry : map.entrySet()) { int pos = entry.getKey(); int spd = entry.getValue(); float time=(float ) (target-pos)/(float )spd; while (!stack.isEmpty()&&time>=stack.peek()){ stack.pop(); System.out.println(stack.size()); } stack.push(time); } return stack.size(); }
Queue 1、add()和offer()区别:
add()和offer()都是向队列中添加一个元素。一些队列有大小限制,因此如果想在一个满的队列中加入一个新项,调用 add() 方法就会抛出一个 unchecked 异常,而调用 offer() 方法会返回 false。因此就可以在程序中进行有效的判断!
2、poll()和remove()区别:
remove() 和 poll() 方法都是从队列中删除第一个元素。如果队列元素为空,调用remove() 的行为与 Collection 接口的版本相似会抛出异常,但是新的 poll() 方法在用空集合调用时只是返回 null。因此新的方法更适合容易出现异常条件的情况。
3、element() 和 peek() 区别:
element() 和 peek() 用于在队列的头部查询元素。与 remove() 方法类似,在队列为空时, element() 抛出一个异常,而 peek() 返回 null。
PriorityQueue 1 2 PriorityQueue<int []> pq = new PriorityQueue <>((pair1, pair2)->pair2[1 ]-pair1[1 ]);
1 2 PriorityQueue<int []> pq = new PriorityQueue <>((pair1,pair2)->pair1[1 ]-pair2[1 ]);
贪心 + 优先队列,在遍历房间的过程中,如果 nums[i]为负数,我们将其放入一个小根堆(优先队列)中。当计算完第 i 个房间的生命值影响后,如果生命值小于等于 0,那么我们取出堆顶元素,表示将该房间调整至末尾,并将其补回生命值中。由于一定会从小根堆中取出一个小于等于 nums[i] 的值,因此调整完成后,生命值一定大于 0。
当所有房间遍历完成后,我们还需要将所有从堆中取出元素的和重新加入生命值,如果生命值小于等于 0,说明无解。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public int magicTower (int [] nums) { Queue<Integer>queue=new PriorityQueue <>(); int cur=1 ; int back=0 ; int res=0 ; for (int num:nums){ if (num<0 )queue.add(num); cur+=num; if (cur<=0 ){ res++; int n=queue.poll(); cur-=n; back+=n; } } cur+=back; return cur>0 ?1 :0 ; }
使用例子利用大小顶堆反复跳实现对于队列的排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 public class MedianFinder { Queue<Integer>min=new PriorityQueue <>(); Queue<Integer>max=new PriorityQueue <>(); public MedianFinder () { min = new PriorityQueue <Integer>((a, b) -> (b - a)); max = new PriorityQueue <Integer>((a, b) -> (a - b)); } public void addNum (int num) { if (min.isEmpty()||num<=min.peek()){ min.offer(num); if (max.size()+1 <min.size()){ max.offer(min.poll()); } } else { max.offer(num); if (min.size()+1 <max.size()){ min.offer(max.poll()); } } } public double findMedian () { if (max.size()<min.size()){ return min.peek(); } return (max.peek()+min.peek())/2.0 ; } }
此题使用PriorityQueue来完成 对于插入数字的排序 为了方便操作并且字符是已经排好序的我们选用字符索引作为priorityqueue的存储数字
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public List<List<Integer>> kSmallestPairs (int [] nums1, int [] nums2, int k) { List<List<Integer>>res=new ArrayList <>(); int m=nums1.length; int n=nums2.length; Queue<int []>queue=new PriorityQueue <>((a,b)->{ return nums1[a[0 ]] + nums2[a[1 ]] - nums1[b[0 ]] - nums2[b[1 ]]; }); for (int i = 0 ; i < Math.min(m, k); i++) { queue.offer(new int []{i,0 }); } while (k-->0 &&!queue.isEmpty()){ int [] idxPair = queue.poll(); List<Integer>group=new ArrayList <>(); group.add(nums1[idxPair[0 ]]); group.add(nums2[idxPair[1 ]]); res.add(group); if (idxPair[1 ]+1 <n){ queue.offer(new int []{idxPair[0 ],idxPair[1 ]+1 }); } } return res; }
辅助栈法 最小栈
按照上面的思路,我们只需要设计一个数据结构,使得每个元素 a 与其相应的最小值 m 时刻保持一一对应。因此我们可以使用一个辅助栈,与元素栈同步插入与删除,用于存储与每个元素对应的最小值。
当一个元素要入栈时,我们取当前辅助栈的栈顶存储的最小值,与当前元素比较得出最小值,将这个最小值插入辅助栈中;
当一个元素要出栈时,我们把辅助栈的栈顶元素也一并弹出;
在任意一个时刻,栈内元素的最小值就存储在辅助栈的栈顶元素中。
字符串解码
构建辅助栈 stack, 遍历字符串 s 中每个字符 c; 当 c 为数字时,将数字字符转化为数字 multi,用于后续倍数计算; 当 c 为字母时,在 res 尾部添加 c; 当 c 为 [ 时,将当前 multi 和 res 入栈,并分别置空置 000: 记录此 [ 前的临时结果 res 至栈,用于发现对应 ] 后的拼接操作; 记录此 [ 前的倍数 multi 至栈,用于发现对应 ] 后,获取 multi × […] 字符串。 进入到新 [ 后,res 和 multi 重新记录。 当 c 为 ] 时,stack 出栈,拼接字符串 res = last_res + cur_multi * res,其中: last_res是上个 [ 到当前 [ 的字符串,例如 “3[a2[c]]” 中的 a; cur_multi是当前 [ 到 ] 内字符串的重复倍数,例如 “3[a2[c]]” 中的 2。 返回字符串 res。
使用辅助的栈帮忙存储每一层的字符结果这样可以将其递归返回到上一层输出
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public String decodeString (String s) { StringBuilder res = new StringBuilder (); int multi = 0 ; LinkedList<Integer> stack_multi = new LinkedList <>(); LinkedList<String> stack_res = new LinkedList <>(); for (Character c : s.toCharArray()) { if (c == '[' ) { stack_multi.addLast(multi); stack_res.addLast(res.toString()); multi = 0 ; res = new StringBuilder (); } else if (c == ']' ) { StringBuilder tmp = new StringBuilder (); int cur_multi = stack_multi.removeLast(); for (int i = 0 ; i < cur_multi; i++) tmp.append(res); res = new StringBuilder (stack_res.removeLast() + tmp); } else if (c >= '0' && c <= '9' ) multi = multi * 10 + Integer.parseInt(c + "" ); else res.append(c); } return res.toString(); }
两种思路如果使用栈则是按照行求
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public int trap (int [] height) { Stack<Integer> st = new Stack <>(); st.push(0 ); int sum = 0 ; for (int i = 1 ; i < height.length; i++) { while (!st.empty() && height[i] > height[st.peek()]) { int mid = st.peek(); st.pop(); if (!st.empty()) { int h = Math.min(height[st.peek()], height[i]) - height[mid]; int w = i - st.peek() - 1 ; sum += h * w; } } st.push(i); } return sum; }
如果使用双指针则是按照列来求, 每次计算相邻两个列的差值只要最右边有高于左边的水就一定留得住
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public int trap (int [] height) { int left=0 ,right=height.length-1 ; int leftheight=height[left],rightheight=height[right]; int leftmax=0 ,rightmax=0 ; int sum=0 ; while (left<=right){ leftmax=Math.max(leftmax,height[left]); rightmax=Math.max(rightmax,height[right]); if (leftmax<rightmax){ sum+=leftmax-height[left]; left++; } else { sum+=rightmax-height[right]; right--; } } return sum; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 public int leastInterval (char [] tasks, int n) { int [] hash = new int [26 ]; for (int i = 0 ; i < tasks.length; ++i) { hash[tasks[i] - 'A' ] += 1 ; } Arrays.sort(hash); int minLen = (n+1 ) * (hash[25 ] - 1 ) + 1 ; for (int i = 24 ; i >= 0 ; --i){ if (hash[i] == hash[25 ]) ++ minLen; } return Math.max(minLen, tasks.length); }
此题思路为银行家算法先从小满足能够获取的资源,然后经可能在最小资源中选取最大的获利
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public int findMaximizedCapital (int k, int w, int [] profits, int [] capital) { int n=profits.length; int curr = 0 ; int eff[][]=new int [n][2 ]; for (int i = 0 ; i <n; i++) { eff[i][0 ]=capital[i]; eff[i][1 ]=profits[i]; } Arrays.sort(eff,(a,b)->{return a[0 ]-b[0 ];}); PriorityQueue<Integer>queue=new PriorityQueue <>((x, y) -> y - x); for (int i = 0 ; i < k; i++) { while (curr<n&&eff[curr][0 ]<=w){ queue.add(eff[curr][1 ]); curr++; } if (!queue.isEmpty()) { w += queue.poll(); } else { break ; } } return w; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 public int calculate (String s) { Deque<Integer> queue = new LinkedList <Integer>(); queue.add(1 ); int pre=1 ; int res=0 ; int i=0 ; while (i<s.length()) { if (s.charAt(i)==' ' )i++; else if (s.charAt(i)=='+' ){ pre=queue.peek(); i++; } else if (s.charAt(i)=='-' ){ pre=-queue.peek(); i++; } else if (s.charAt(i)=='(' ){ queue.push(pre); i++; } else if (s.charAt(i)==')' ) { queue.pop(); i++; } else { long num=0 ; while (i<s.length()&&Character.isDigit(s.charAt(i))){ num=num*10 +s.charAt(i)-'0' ; i++; } res+=num*pre; } } return res; }
计算器类题通用模版
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 class Solution { Map<Character, Integer> map = new HashMap <>(){{ put('-' , 1 ); put('+' , 1 ); put('*' , 2 ); put('/' , 2 ); put('%' , 2 ); put('^' , 3 ); }}; public int calculate (String s) { s = s.replaceAll(" " , "" ); char [] cs = s.toCharArray(); int n = s.length(); Deque<Integer> nums = new ArrayDeque <>(); nums.addLast(0 ); Deque<Character> ops = new ArrayDeque <>(); for (int i = 0 ; i < n; i++) { char c = cs[i]; if (c == '(' ) { ops.addLast(c); } else if (c == ')' ) { while (!ops.isEmpty()) { if (ops.peekLast() != '(' ) { calc(nums, ops); } else { ops.pollLast(); break ; } } } else { if (isNumber(c)) { int u = 0 ; int j = i; while (j < n && isNumber(cs[j])) u = u * 10 + (cs[j++] - '0' ); nums.addLast(u); i = j - 1 ; } else { if (i > 0 && (cs[i - 1 ] == '(' || cs[i - 1 ] == '+' || cs[i - 1 ] == '-' )) { nums.addLast(0 ); } while (!ops.isEmpty() && ops.peekLast() != '(' ) { char prev = ops.peekLast(); if (map.get(prev) >= map.get(c)) { calc(nums, ops); } else { break ; } } ops.addLast(c); } } } while (!ops.isEmpty()) calc(nums, ops); return nums.peekLast(); } void calc (Deque<Integer> nums, Deque<Character> ops) { if (nums.isEmpty() || nums.size() < 2 ) return ; if (ops.isEmpty()) return ; int b = nums.pollLast(), a = nums.pollLast(); char op = ops.pollLast(); int ans = 0 ; if (op == '+' ) ans = a + b; else if (op == '-' ) ans = a - b; else if (op == '*' ) ans = a * b; else if (op == '/' ) ans = a / b; else if (op == '^' ) ans = (int )Math.pow(a, b); else if (op == '%' ) ans = a % b; nums.addLast(ans); } boolean isNumber (char c) { return Character.isDigit(c); } }
二叉树 递归三要素
确定递归函数的参数和返回值: 确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。确定终止条件: 写完了递归算法, 运行的时候,经常会遇到栈溢出的错误,就是没写终止条件或者终止条件写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出。确定单层递归的逻辑: 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。
1、树的遍历方式 递归实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 void postorder (TreeNode root, List<Integer> list) { if (root==null ){ return ; } postorder(root.left,list); postorder(root.right,list); list.add(root.val); } void frontorder (TreeNode root, List<Integer> list) { if (root==null ) return ; list.add(root.val); frontorder(root.left,list); frontorder(root.right,list); } void midorder (TreeNode root, List<Integer> list) { if (root==null ) return ; midorder(root.left,list); list.add(root.val); frontorder(root.right,list); }
迭代实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 public List<Integer> preorderTraversal (TreeNode root) { List<Integer> result = new ArrayList <>(); if (root == null ){ return result; } Stack<TreeNode> stack = new Stack <>(); stack.push(root); while (!stack.isEmpty()){ TreeNode node = stack.pop(); result.add(node.val); if (node.right != null ){ stack.push(node.right); } if (node.left != null ){ stack.push(node.left); } } return result; } } public List<Integer> inorderTraversal (TreeNode root) { List<Integer> result = new ArrayList <>(); if (root == null ){ return result; } Stack<TreeNode> stack = new Stack <>(); TreeNode cur = root; while (cur != null || !stack.isEmpty()){ if (cur != null ){ stack.push(cur); cur = cur.left; }else { cur = stack.pop(); result.add(cur.val); cur = cur.right; } } return result; } public List<Integer> postorderTraversal (TreeNode root) { List<Integer> result = new ArrayList <>(); if (root == null ){ return result; } Stack<TreeNode> stack = new Stack <>(); stack.push(root); while (!stack.isEmpty()){ TreeNode node = stack.pop(); result.add(node.val); if (node.left != null ){ stack.push(node.left); } if (node.right != null ){ stack.push(node.right); } } Collections.reverse(result); return result; }
层序遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public List<List<Integer>> findBottomLeftValue (TreeNode root) { List<List<Integer>> resList = new ArrayList <List<Integer>>(); if (root == null ) return null ; Queue<TreeNode> que = new LinkedList <TreeNode>(); que.offer(root); while (!que.isEmpty()) { List<Integer> itemList = new ArrayList <Integer>(); int len = que.size(); while (len > 0 ) { TreeNode tmpNode = que.poll(); itemList.add(tmpNode.val); if (tmpNode.left != null ) que.offer(tmpNode.left); if (tmpNode.right != null ) que.offer(tmpNode.right); len--; } resList.add(itemList); } return resList; }
Ps:层序遍历变种 请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以此类推。
使用LinkedList实现对于队列的反转插入
1 2 3 if (!isEven) item.addLast(root.val); else item.addFirst(root.val);
958. 二叉树的完全性检验
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public boolean isCompleteTree (TreeNode root) { Deque<TreeNode> deque = new LinkedList <>(); deque.addLast(root); boolean flag = true ; while (!deque.isEmpty()){ TreeNode node = deque.pollLast(); if (node == null ){ flag = false ; } else { if (!flag){ return false ; } deque.addFirst(node.left); deque.addFirst(node.right); } } return true ; }
两个类型一致的题目关键点在于先从先序遍历/后序遍历找到树的头结点 然后再去拆分其左右子树范围再递归创建左右子树
1 2 3 4 5 6 7 8 9 10 11 #后序 if (inBegin >= inEnd || postBegin >= postEnd) { return null ; } int rootIndex = map.get(postorder[postEnd - 1 ]); TreeNode root = new TreeNode (inorder[rootIndex]); int lenOfLeft = rootIndex - inBegin; root.left = findNode(inorder, inBegin, rootIndex, postorder, postBegin, postBegin + lenOfLeft); root.right = findNode(inorder, rootIndex + 1 , inEnd, postorder, postBegin + lenOfLeft, postEnd - 1 );
1 2 3 4 5 6 7 8 9 10 11 #先序 if (preBegin >= preEnd || inBegin >= inEnd) { return null ; } int rootIndex = map.get(preorder[preBegin]); TreeNode root = new TreeNode (inorder[rootIndex]); int lenOfLeft = rootIndex - inBegin; root.left = findNode(preorder, preBegin + 1 , preBegin + lenOfLeft + 1 , inorder, inBegin, rootIndex); root.right = findNode(preorder, preBegin + lenOfLeft + 1 , preEnd, inorder, rootIndex + 1 , inEnd);
其中 preorder 是一个具有 无重复 值的二叉树的前序遍历,postorder 是同一棵树的后序遍历
树可以构造,答案不唯一 也是找到后序遍历切入点找到左右子树长度创建
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public TreeNode constructFromPrePost (int [] preorder, int [] postorder) { int n = preorder.length; Map<Integer, Integer> postMap = new HashMap <Integer, Integer>(); for (int i = 0 ; i < n; i++) { postMap.put(postorder[i], i); } return dfs(preorder, postorder, postMap, 0 , n - 1 , 0 , n - 1 ); } public TreeNode dfs (int [] preorder, int [] postorder, Map<Integer, Integer> postMap, int preLeft, int preRight, int postLeft, int postRight) { if (preLeft > preRight) { return null ; } int leftCount = 0 ; if (preLeft < preRight) { leftCount = postMap.get(preorder[preLeft + 1 ]) - postLeft + 1 ; } return new TreeNode (preorder[preLeft], dfs(preorder, postorder, postMap, preLeft + 1 , preLeft + leftCount, postLeft, postLeft + leftCount - 1 ), dfs(preorder, postorder, postMap, preLeft + leftCount + 1 , preRight, postLeft + leftCount, postRight - 1 )); }
此题使用两遍dfs 第一遍算出每一层的节点值的和,第二次dfs时用每层和减去本节点的非兄弟节点的值的和就是替换的兄弟节点值的和
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 List<Integer>sum=new ArrayList <>(); public TreeNode replaceValueInTree (TreeNode root) {dfs1(root,0 ); root.val=0 ; dfs2(root,0 ); return root;} public void dfs1 (TreeNode root,int depth) { if (root==null )return ; if (sum.size()<=depth) { sum.add(0 ); } sum.set(depth, sum.get(depth) + root.val); dfs1(root.left, depth + 1 ); dfs1(root.right, depth + 1 ); } public void dfs2 (TreeNode node,int depth) { int l=node.left==null ?0 :node.left.val; int r=node.right==null ?0 :node.right.val; int add=l+r; depth++; if (node.left!=null ){ node.left.val=sum.get(depth)-add; dfs2(node.left,depth); } if (node.right!=null ){ node.right.val=sum.get(depth)-add; dfs2(node.right,depth); } }
此题思想是从下层的子节点的祖先找起一层层返回判断左右节点是否都存在公共祖先如果存在则返回当前节点,如果不存在返回存在节点的祖先
1 2 3 4 5 6 7 8 9 public TreeNode lowestCommonAncestor (TreeNode root, TreeNode p, TreeNode q) { if (root==p||root==q||root==null )return root; TreeNode left=lowestCommonAncestor(root.left,p,q); TreeNode right=lowestCommonAncestor(root.right,p,q); if (left!=null &&right!=null )return root; else if (left==null &&right!=null )return right; else if (left!=null &&right==null )return left; else return null ; }
具体做法是,对于当前节点,如果其左子节点不为空,则在其左子树中找到最右边的节点,作为前驱节点,将当前节点的右子节点赋给前驱节点的右子节点,然后将当前节点的左子节点赋给当前节点的右子节点,并将当前节点的左子节点设为空。对当前节点处理结束后,继续处理链表中的下一个节点,直到所有节点都处理结束.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 1 / \ 2 5 / \ \ 3 4 6 1 \ 2 5 / \ \ 3 4 6 1 \ 2 / \ 3 4 \ 5 \ 6 1 \ 2 \ 3 4 \ 5 \ 6 1 \ 2 \ 3 \ 4 \ 5 \ 6
1 2 3 4 5 6 7 8 9 10 11 12 public void flatten (TreeNode root) { while (root !=null ){ if (root.left!=null ){ TreeNode pre = root.left; while (pre.right!=null )pre=pre.right; pre.right=root.right; root.right=root.left; root.left=null ; } root=root.right; } }
2、特殊二叉树 完全二叉树 在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2^(h-1) 个节点。
大家要自己看完全二叉树的定义,很多同学对完全二叉树其实不是真正的懂了。
我来举一个典型的例子如题:
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
对于情况一,可以直接用 2^树深度 - 1 来计算,注意这里根节点深度为1。
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
1 2 3 4 5 6 7 8 9 public int minIncrements (int n, int [] cost) { int ans = 0 ; for (int i = n - 2 ; i > 0 ; i -= 2 ) { ans += Math.abs(cost[i] - cost[i + 1 ]); cost[i / 2 ] += Math.max(cost[i], cost[i + 1 ]); } return ans; }
平衡二叉树 一棵度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
二叉搜索树 二叉搜索树 前面介绍的树,都没有数值的,而二叉搜索树是有数值的了,二叉搜索树是一个有序树 。意味着中序遍历是一个顺序递增数组
若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
它的左、右子树也分别为二叉排序树
下面这两棵树都是搜索树
数组构建二叉搜索树 1 2 3 4 5 6 7 8 9 10 11 public TreeNode constructMaximumBinaryTree2 (int [] nums, int leftIndex, int rightIndex) { if (rightIndex - leftIndex < 0 ) { return null ; } int maxVal=(leftIndex+rightIndex)/2 ; TreeNode root = new TreeNode (nums[maxVal]); root.left = constructMaximumBinaryTree2(nums, leftIndex, (leftIndex+rightIndex)/2 -1 ); root.right = constructMaximumBinaryTree2(nums, (leftIndex+rightIndex)/2 +1 , rightIndex); return root; }
3、计算节点数/深度
递归的思想
1 2 3 int leftdepth = getdepth(node->left); int rightdepth = getdepth(node->right); int depth = 1 + Math.max(leftdepth, rightdepth);
Ps:在选择边界时尽量使用统一选择要么都左闭右开要么右闭左开
来看一下一共分几步:
第一步:如果数组大小为零的话,说明是空节点了。
第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
第五步:切割后序数组,切成后序左数组和后序右数组
第六步:递归处理左区间和右区间
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 Map<Integer, Integer> map; public TreeNode buildTree (int [] inorder, int [] postorder) { map = new HashMap <>(); for (int i = 0 ; i < inorder.length; i++) { map.put(inorder[i], i); } return findNode(inorder, 0 , inorder.length, postorder,0 , postorder.length); } public TreeNode findNode (int [] inorder, int inBegin, int inEnd, int [] postorder, int postBegin, int postEnd) { if (inBegin >= inEnd || postBegin >= postEnd) { return null ; } int rootIndex = map.get(postorder[postEnd - 1 ]); TreeNode root = new TreeNode (inorder[rootIndex]); int lenOfLeft = rootIndex - inBegin; root.left = findNode(inorder, inBegin, rootIndex, postorder, postBegin, postBegin + lenOfLeft); root.right = findNode(inorder, rootIndex + 1 , inEnd, postorder, postBegin + lenOfLeft, postEnd - 1 ); return root; } public TreeNode findNode (int [] preorder, int preBegin, int preEnd, int [] inorder, int inBegin, int inEnd) { if (preBegin >= preEnd || inBegin >= inEnd) { return null ; } int rootIndex = map.get(preorder[preBegin]); TreeNode root = new TreeNode (inorder[rootIndex]); int lenOfLeft = rootIndex - inBegin; root.left = findNode(preorder, preBegin + 1 , preBegin + lenOfLeft + 1 , inorder, inBegin, rootIndex); root.right = findNode(preorder, preBegin + lenOfLeft + 1 , preEnd, inorder, rootIndex + 1 , inEnd); return root; }
根据二叉搜索树的性质
如果目标节点大于当前节点值,则去右子树中删除;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 if (root == null ) return null ;if (root.val > key) { root.left = deleteNode(root.left,key); } else if (root.val < key) { root.right = deleteNode(root.right,key); } else { if (root.left==null )return root.right; if (root.right==null )return root.left; TreeNode rootleft=root.left; TreeNode rootright=root.right; while (rootright.left!=null )rootright=rootright.left; rootright.left=rootleft; root=root.right; } return root;
注意此处中序遍历后有个变式的二分查找,我们需要使用n和-1来判断该元素是否超出界限。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 public List<List<Integer>> closestNodes (TreeNode root, List<Integer> queries) { List<Integer> arr = new ArrayList <>(); dfs(root, arr); int n = arr.size(); int [] a = new int [n]; for (int i = 0 ; i < n; i++) { a[i] = arr.get(i); } List<List<Integer>> ans = new ArrayList <>(queries.size()); for (int q : queries) { int j = binarysearch(a, q); int mx = j == n ? -1 : a[j]; if (j == n || a[j] != q) { j--; } int mn = j < 0 ? -1 : a[j]; ans.add(new ArrayList <Integer>(Arrays.asList(mn,mx))); } return ans; } private void dfs (TreeNode node, List<Integer> a) { if (node == null ) { return ; } dfs(node.left, a); a.add(node.val); dfs(node.right, a); } public int binarysearch (int a[],int target) { int left=-1 ,right=a.length; while (left+1 <right){ int mid=left+(right-left)/2 ; if (a[mid]>=target)right=mid; else { left=mid; } } return right; }
方法三:BFS+链表
所以在 BFS 的时候,可以一边遍历当前层的节点,一边把下一层的节点连接起来。这样就无需存储下一层的节点了,只需要拿到下一层链表的头节点。
算法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public Node connect (Node root) { Node dum=new Node (); Node cur=root; while (cur!=null ){ dum.next=null ; Node temp=dum; while (cur!=null ){ if (cur.left!=null ){ temp.next=cur.left; temp=temp.next; } if (cur.right!=null ){ temp.next=cur.right; temp=temp.next; } cur=cur.next; } cur=dum.next; } return root; }
前缀树就是自己生成一个树使得这个数能够存储一段String,并且在之后输入时能够判断String的前缀是否吻合或者String是否相同
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 private Trie []children; private boolean isEnd; public Trie () { children=new Trie [26 ]; isEnd=false ; } public void insert (String word) { Trie node=this ; for (int i = 0 ; i < word.length(); i++) { char t=word.charAt(i); if (node.children[t-'a' ]==null ){ node.children[t-'a' ]=new Trie (); } node=node.children[t-'a' ]; } node.isEnd=true ; } public Trie presearch (String word) { Trie node=this ; for (int i = 0 ; i < word.length(); i++) { char t=word.charAt(i); if (node.children[t-'a' ]==null ) return null ; node=node.children[t-'a' ]; } return node; }
变式 211. 添加与搜索单词 - 数据结构设计
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public boolean search (WordDictionary dic,String word,int length) { int n=word.length(); if (length==n)return dic.isEnd; char t=word.charAt(length); if (t!='.' ){ WordDictionary item = dic.children[t-'a' ]; return item!=null && search(item,word,length+1 ); } for (int j = 0 ; j < 26 ; j++){ if (dic.children[j]!=null && search(dic.children[j],word,length+1 )) return true ; } return false ; }
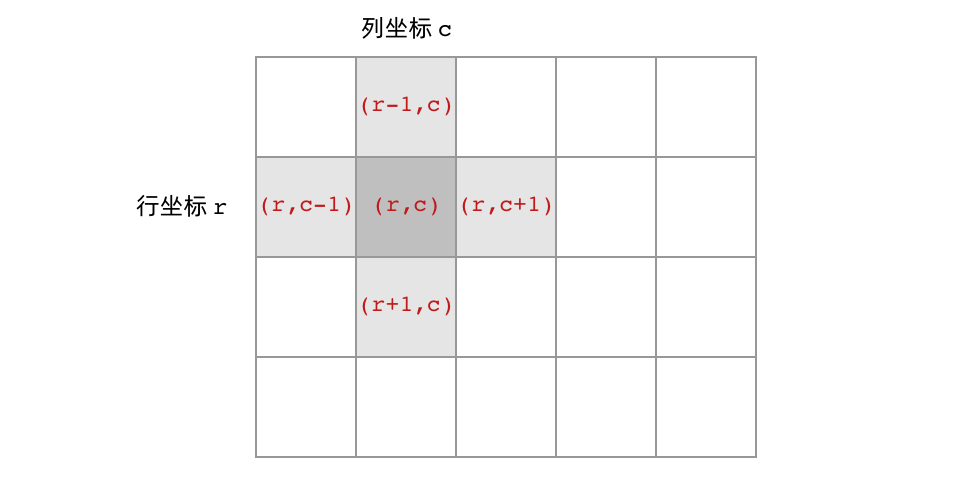
遍历二维网格中的所有单元格。
深度优先搜索所有从当前正在遍历的单元格出发的、由相邻且不重复的单元格组成的路径。因为题目要求同一个单元格内的字母在一个单词中不能被重复使用;所以我们在深度优先搜索的过程中,每经过一个单元格,都将该单元格的字母临时修改为特殊字符(例如 #),以避免再次经过该单元格。
如果当前路径是 words\textit{words}words 中的单词,则将其添加到结果集中。如果当前路径是 wordswordswords 中任意一个单词的前缀,则继续搜索;反之,如果当前路径不是 wordswordswords 中任意一个单词的前缀,则剪枝。我们可以将 words\textit{words}words 中的所有字符串先添加到前缀树中,而后用 O(∣S∣)O(|S|)O(∣S∣) 的时间复杂度查询当前路径是否为 words\textit{words}words 中任意一个单词的前缀。
之后再回溯,因为同一个单词可能在多个不同的路径中出现,所以我们需要使用哈希集合对结果集去重。
在回溯的过程中,我们不需要每一步都判断完整的当前路径是否是 words中任意一个单词的前缀;而是可以记录下路径中每个单元格所对应的前缀树结点,每次只需要判断新增单元格的字母是否是上一个单元格对应前缀树结点的子结点即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 int [][] dirs = {{1 , 0 }, {-1 , 0 }, {0 , 1 }, {0 , -1 }}; public List<String> findWords (char [][] board, String[] words) { Trie2 trie = new Trie2 (); for (String word : words) { trie.insert(word); } Set<String> ans = new HashSet <String>(); for (int i = 0 ; i < board.length; ++i) { for (int j = 0 ; j < board[0 ].length; ++j) { dfs(board, trie, i, j, ans); } } return new ArrayList <String>(ans); } public void dfs (char [][] board, Trie2 now, int i1, int j1, Set<String> ans) { if (!now.children.containsKey(board[i1][j1])) { return ; } char ch = board[i1][j1]; Trie2 nxt = now.children.get(ch); if (!"" .equals(nxt.word)) { ans.add(nxt.word); nxt.word = "" ; } if (!nxt.children.isEmpty()) { board[i1][j1] = '#' ; for (int [] dir : dirs) { int i2 = i1 + dir[0 ], j2 = j1 + dir[1 ]; if (i2 >= 0 && i2 < board.length && j2 >= 0 && j2 < board[0 ].length) { dfs(board, nxt, i2, j2, ans); } } board[i1][j1] = ch; } if (nxt.children.isEmpty()) { now.children.remove(ch); } } } class Trie2 { String word; Map<Character, Trie2> children; boolean isWord; public Trie2 () { this .word = "" ; this .children = new HashMap <Character, Trie2>(); } public void insert (String word) { Trie2 cur = this ; for (int i = 0 ; i < word.length(); ++i) { char c = word.charAt(i); if (!cur.children.containsKey(c)) { cur.children.put(c, new Trie2 ()); } cur = cur.children.get(c); } cur.word = word; }
我们需要按照优先级「“列号从小到大”,对于同列节点,“行号从小到大”,对于同列同行元素,“节点值从小到大”」进行答案构造。
因此我们可以对树进行遍历,遍历过程中记下这些信息 (col,row,val)(col, row, val)(col,row,val),然后根据规则进行排序,并构造答案。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 Map<TreeNode ,int []> map= new HashMap <>(); public List<List<Integer>> verticalTraversal (TreeNode root) { List<List<Integer>>res=new ArrayList <>(); map.put(root,new int []{0 ,0 ,root.val}); dfs(root); List<int []> list = new ArrayList <>(map.values()); Collections.sort(list,(a,b)->{ if (a[0 ]!=b[0 ])return a[0 ]-b[0 ]; if (a[1 ]!=b[1 ])return a[1 ]-b[1 ]; return a[2 ]-b[2 ]; }); for (int i = 0 ; i < list.size();) { int j=i; List<Integer>cur=new ArrayList <>(); while (j<list.size()&&list.get(j)[0 ]==list.get(i)[0 ])cur.add(list.get(j++)[2 ]); res.add(cur); i=j; } return res; } public void dfs (TreeNode root) { if (root==null )return ; int []node=map.get(root); int col=node[0 ],row=node[1 ],val=node[2 ]; if (root.left!=null ){ map.put(root.left, new int []{col - 1 , row + 1 , root.left.val}); dfs(root.left); } if (root.right != null ) { map.put(root.right, new int []{col + 1 , row + 1 , root.right.val}); dfs(root.right); } }
回溯 回溯法模板 回溯函数伪代码如下:
既然是树形结构,那么我们在讲解二叉树的递归 (opens new window) 的时候,就知道遍历树形结构一定要有终止条件。
所以回溯也有要终止条件。
什么时候达到了终止条件,树中就可以看出,一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
所以回溯函数终止条件伪代码如下:
1 2 3 4 if (终止条件) { 存放结果; return ; }
在上面我们提到了,回溯法一般是在集合中递归搜索,集合的大小构成了树的宽度,递归的深度构成的树的深度。
回溯函数遍历过程伪代码如下:
1 2 3 4 5 for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) { 处理节点; backtracking(路径,选择列表); 回溯,撤销处理结果 }
分析完过程,回溯算法模板框架如下:
1 2 3 4 5 6 7 8 9 10 11 12 void backtracking (参数) { if (终止条件) { 存放结果; return ; } for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) { 处理节点; backtracking(路径,选择列表); 回溯,撤销处理结果 } }
这份模板很重要,后面做回溯法的题目都靠它了!
回溯法解决的问题 回溯法,一般可以解决如下几种问题:
组合问题:N个数里面按一定规则找出k个数的集合
1 2 3 4 5 6 7 8 9 10 11 12 private void combineHelper (int n, int k, int startIndex) { if (path.size() == k){ result.add(new ArrayList <>(path)); return ; } for (int i = startIndex; i <= n - (k - path.size()) + 1 ; i++){ path.add(i); combineHelper(n, k, i + 1 ); path.removeLast(); } }
切割问题:一个字符串按一定规则有几种切割方式
1 2 3 4 5 6 7 8 9 10 11 12 for (int i = startIndex; i < s.length(); i++) { if (isPalindrome(s, startIndex, i)) { String str = s.substring(startIndex, i + 1 ); deque.addLast(str); } else { continue ; } backTracking(s, i + 1 ); deque.removeLast(); }
子集问题:一个N个数的集合里有多少符合条件的子集
如果把 子集问题、组合问题、分割问题都抽象为一棵树的话,那么组合问题和分割问题都是收集树的叶子节点,而子集问题是找树的所有节点!
其实子集也是一种组合问题,因为它的集合是无序的,子集{1,2} 和 子集{2,1}是一样的。
那么既然是无序,取过的元素不会重复取,写回溯算法的时候,for就要从startIndex开始,而不是从0开始!
1 2 3 4 5 6 7 8 9 10 11 private void subsetsHelper (int [] nums, int startIndex) { result.add(new ArrayList <>(path)); if (startIndex >= nums.length){ return ; } for (int i = startIndex; i < nums.length; i++){ path.add(nums[i]); subsetsHelper(nums, i + 1 ); path.removeLast(); } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 private void backTrack (int [] nums, boolean [] used) { if (path.size() == nums.length) { result.add(new ArrayList <>(path)); return ; } for (int i = 0 ; i < nums.length; i++) { if (i > 0 && nums[i] == nums[i - 1 ] && used[i - 1 ] == false ) { continue ; } if (used[i] == false ) { used[i] = true ; path.add(nums[i]); backTrack(nums, used); path.remove(path.size() - 1 ); used[i] = false ; } } }
剑指 Offer 36. 二叉搜索树与双向链表 思路主要掌握二叉搜索树的中序遍历过程以及双向链表的创建方式
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 Node pre,head; public Node treeToDoublyList (Node root) { if (root==null )return head; dfs2(root); pre.right=head; head.left=pre; return head; } public void dfs2 (Node cur) { if (cur==null )return ; dfs2(cur.left); if (pre != null ) pre.right = cur; else head = cur; cur.left=pre; pre=cur; dfs2(cur.right); }
二叉树的最近公共祖先 二叉树遍历从下到上依靠的就是回溯算法
1 2 3 4 5 6 7 8 9 public TreeNode lowestCommonAncestor2 (TreeNode root, TreeNode p, TreeNode q) { if (root==p||root==q||root==null )return root; TreeNode left=lowestCommonAncestor2(root.left,p,q); TreeNode right=lowestCommonAncestor2(root.right,p,q); if (left!=null &&right!=null )return root; else if (left==null &&right!=null )return right; else if (left!=null &&right==null )return left; else return null ; }
N皇后 这里我明确给出了棋盘的宽度就是for循环的长度,递归的深度就是棋盘的高度,这样就可以套进回溯法的模板里了 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 List<List<String>> result4 = new ArrayList <>(); public List<List<String>> solveNQueens (int n) { char [][] chessboard = new char [n][n]; for (char [] c : chessboard) { Arrays.fill(c, '.' ); } queensHelper(chessboard, 0 ,n ); return result4; } public void queensHelper (char [][]chessboard,int row,int n) { if (row==n){ result4.add(Array2List(chessboard)); return ; } for (int col = 0 ; col < n; col++) { if (isValid(row,col,n,chessboard)){ chessboard[row][col]='Q' ; queensHelper(chessboard,row+1 ,n); chessboard[row][col]='.' ; } } } public List Array2List (char [][] chessboard) { List<String> list = new ArrayList <>(); for (char [] c : chessboard) { list.add(String.copyValueOf(c)); } return list; } public boolean isValid (int row, int col, int n, char [][] chessboard) { for (int i = 0 ; i < row; i++) { if (chessboard[i][col]=='Q' )return false ; } for (int i=row-1 , j=col-1 ; i>=0 && j>=0 ; i--, j--) { if (chessboard[i][j] == 'Q' ) { return false ; } } for (int i=row-1 , j=col+1 ; i>=0 && j<=n-1 ; i--, j++) { if (chessboard[i][j] == 'Q' ) { return false ; } } return true ; }
DFS与BFS dfs是由底下遍历到上层,而bfs是由上层依次遍历到底层
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 public int maxDepth (TreeNode root) { if (root==null )return 0 ; int nLeft = maxDepth(root.left); int nRight = maxDepth(root.right); return nLeft > nRight ? nLeft + 1 : nRight + 1 ; } public int maxDepth (TreeNode root) { if (root == null ) return 0 ; Queue<TreeNode> queue = new LinkedList <>(); queue.add(root); int res = 0 ; while (!queue.isEmpty()) { res++; int n = queue.size(); for (int i = 0 ; i < n; i++) { TreeNode node = queue.poll(); if (node.left != null ) queue.add(node.left); if (node.right != null ) queue.add(node.right); } } return res; }
前缀和,递归,回溯 在同一个路径之下(可以理解成二叉树从root节点出发,到叶子节点的某一条路径),如果两个数的前缀总和是相同的,那么这些节点之间的元素总和为零。进一步扩展相同的想法,如果前缀总和currSum,在节点A和节点B处相差target,则位于节点A和节点B之间的元素之和是target。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 public int pathSum (TreeNode root, int sum) { Map<Long, Integer> prefixSumCount = new HashMap <>(); prefixSumCount.put(0L , 1 ); return recursionPathSum(root, prefixSumCount, sum, 0L ); } private int recursionPathSum (TreeNode node, Map<Long, Integer> prefixSumCount, int target, long currSum) { if (node == null ) { return 0 ; } int res = 0 ; currSum += node.val;- res += prefixSumCount.getOrDefault(currSum - target, 0 ); prefixSumCount.put(currSum, prefixSumCount.getOrDefault(currSum, 0 ) + 1 ); res += recursionPathSum(node.left, prefixSumCount, target, currSum); res += recursionPathSum(node.right, prefixSumCount, target, currSum); prefixSumCount.put(currSum, prefixSumCount.get(currSum) - 1 ); return res; }
例如,考虑如下二叉树。
-10
得到叶节点的最大贡献值之后,再计算非叶节点的最大贡献值。节点 202020 的最大贡献值等于 20+max(15,7)=3520+\max(15,7)=3520+max(15,7)=35,节点 −10-10−10 的最大贡献值等于 −10+max(9,35)=25-10+\max(9,35)=25−10+max(9,35)=25。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 int maxsum=Integer.MIN_VALUE;; public int maxPathSum (TreeNode root) { dfs(root); return maxsum; } public int dfs (TreeNode root) { if (root==null ) return 0 ; int leftgain=Math.max(dfs(root.left),0 ); int rightgain=Math.max(dfs(root.right),0 ); int sum=root.val+leftgain+rightgain; maxsum=Math.max(sum,maxsum); return root.val + Math.max(leftgain, rightgain); }
此题关键点在于排序后如何找到分割点,这样的话对于小于的我们用long left=(long) q * j - sum[j];大于的我们用long right=sum[n]-sum[j]-(long) q * (n - j);
通过前缀和我来求得一系列的元素总和
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 public List<Long> minOperations (int [] nums, int [] queries) { Arrays.sort(nums); int n = nums.length; long [] sum = new long [n + 1 ]; for (int i = 0 ; i < n; ++i) sum[i + 1 ] = sum[i] + nums[i]; List<Long> ans = new ArrayList <Long>(queries.length); for (int q:queries) { int j=search(nums,q); long left=(long ) q * j - sum[j]; long right=sum[n]-sum[j]-(long ) q * (n - j); ans.add(left+right); } return ans; } public int search (int nums[],int tar) { int left=0 ,right=nums.length-1 ; while (left<=right){ int mid=left+(right-left)/2 ; if (nums[mid]<tar)left=mid+1 ; else right=mid-1 ; } return left; }
这两题思路相似都是处理括号有效的问题
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution { List<String>result=new ArrayList <>(); public List<String> generateParenthesis (int n) { dfs("" ,n,n); return result; } public void dfs (String cur,int left,int right) { if (left==0 &&right==0 ){ result.add(cur); return ; } if (left > right) { return ; } if (left>0 ){ dfs(cur+"(" ,left-1 ,right); } if (right>0 ){ dfs(cur+")" ,left,right-1 ); } } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 class Solution { private List<String> res = new ArrayList <String>(); public List<String> removeInvalidParentheses (String s) { int lremove = 0 ; int rremove = 0 ; for (int i = 0 ; i < s.length(); i++) { if (s.charAt(i) == '(' ) { lremove++; } else if (s.charAt(i) == ')' ) { if (lremove == 0 ) { rremove++; } else { lremove--; } } } helper(s, 0 , lremove, rremove); return res; } private void helper (String str, int start, int lremove, int rremove) { if (lremove == 0 && rremove == 0 ) { if (isValid(str)) { res.add(str); } return ; } for (int i = start; i < str.length(); i++) { if (i != start && str.charAt(i) == str.charAt(i - 1 )) { continue ; } if (lremove + rremove > str.length() - i) { return ; } if (lremove > 0 && str.charAt(i) == '(' ) { helper(str.substring(0 , i) + str.substring(i + 1 ), i, lremove - 1 , rremove); } if (rremove > 0 && str.charAt(i) == ')' ) { helper(str.substring(0 , i) + str.substring(i + 1 ), i, lremove, rremove - 1 ); } } } private boolean isValid (String str) { int cnt = 0 ; for (int i = 0 ; i < str.length(); i++) { if (str.charAt(i) == '(' ) { cnt++; } else if (str.charAt(i) == ')' ) { cnt--; if (cnt < 0 ) { return false ; } } } return cnt == 0 ; } }
二维前缀和
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 int [][] sum; public NumMatrix (int [][] matrix) { int n = matrix.length, m = n == 0 ? 0 : matrix[0 ].length; sum = new int [n + 1 ][m + 1 ]; for (int i = 1 ; i <= n; i++) { for (int j = 1 ; j <= m; j++) { sum[i][j] = sum[i - 1 ][j] + sum[i][j - 1 ] - sum[i - 1 ][j - 1 ] + matrix[i - 1 ][j - 1 ]; } } } public int sumRegion (int x1, int y1, int x2, int y2) { x1++; y1++; x2++; y2++; return sum[x2][y2] - sum[x1 - 1 ][y2] - sum[x2][y1 - 1 ] + sum[x1 - 1 ][y1 - 1 ]; }
动态规划 动态规划的解题步骤
确定dp数组(dp table)以及下标的含义 确定递推公式 dp数组如何初始化 确定遍历顺序 举例推导dp数组
此题思想在于不以(来计算有效个数而是以)来计算有效个数
1 2 3 4 5 6 7 8 9 if (s.charAt(i) == ')' ) { if (s.charAt(i - 1 ) == '(' ) { dp[i] = (i >= 2 ? dp[i - 2 ] : 0 ) + 2 ; } else if (i - dp[i - 1 ] > 0 && s.charAt(i - dp[i - 1 ] - 1 ) == '(' ) { dp[i] = dp[i - 1 ] + ((i - dp[i - 1 ]) >= 2 ? dp[i - dp[i - 1 ] - 2 ] : 0 ) + 2 ; } maxans = Math.max(maxans, dp[i]); }
1.当 nums[i]>nums[j] 时: nums[i] 可以接在nums[j] 之后(此题要求严格递增),此情况下最长上升子序列长度为dp[j]+1 ;
转移方程为 dp[i] = max(dp[i], dp[j] + 1) for j in [0, i)
优化方式将长度变化g寻找递增元素值, 如果num[i]>g中的最后一个元素值时长度增加将其添加,如果小于则去更新g中第一个大于num[i]的值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 public int lengthOfLIS (int [] nums) { if (nums.length == 0 ) return 0 ; int [] dp = new int [nums.length]; int res = 0 ; Arrays.fill(dp, 1 ); for (int i = 0 ; i < nums.length; i++) { for (int j = 0 ; j < i; j++) { if (nums[j] < nums[i]) dp[i] = Math.max(dp[i], dp[j] + 1 ); } res = Math.max(res, dp[i]); } return res; } public int lengthOfLIS (int [] nums) { int [] tails = new int [nums.length]; int res = 0 ; for (int num : nums) { int i = 0 , j = res; while (i < j) { int m = (i + j) / 2 ; if (tails[m] < num) i = m + 1 ; else j = m; } tails[i] = num; if (res == j) res++; } return res; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class Solution {public int minimumMountainRemovals (int [] nums) { int n = nums.length; int [] pre = getLISArray(nums); int [] reversed = reverse(nums); int [] suf = getLISArray(reversed); suf = reverse(suf); int ans = 0 ; for (int i = 0 ; i < n; ++i) { if (pre[i] > 1 && suf[i] > 1 ) { ans = Math.max(ans, pre[i] + suf[i] - 1 ); } } return n - ans; } public int [] getLISArray(int [] nums) { int n = nums.length; int [] dp = new int [n]; Arrays.fill(dp, 1 ); for (int i = 0 ; i < n; ++i) { for (int j = 0 ; j < i; ++j) { if (nums[j] < nums[i]) { dp[i] = Math.max(dp[i], dp[j] + 1 ); } } } return dp; } public int [] reverse(int [] nums) { int n = nums.length; int [] reversed = new int [n]; for (int i = 0 ; i < n; i++) { reversed[i] = nums[n - 1 - i]; } return reversed; } }
第一种情况:这个子数组不是环状的,就是说首尾不相连。
1 2 3 4 5 6 7 8 9 10 11 12 public int maxSubarraySumCircular (int [] nums) { int n=nums.length,total=0 ; int max=0 ,maxsum=nums[0 ],min=0 ,minsum=nums[0 ]; for (int i = 0 ; i < n; i++) { max=Math.max(max+nums[i],nums[i]); maxsum=Math.max(max,maxsum); min=Math.min(min+nums[i],nums[i]); maxsum=Math.min(min,minsum); total+=nums[i]; } return maxsum > 0 ? Math.max(maxsum, total - minsum) : maxsum; }
动态规划加滑动窗口,使用一个queue来负责记录最大的取值的位置 dp数组为走到当前位置能获取的最大分数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public int maxResult (int [] nums, int k) { int n = nums.length; int [] dp = new int [n]; dp[0 ] = nums[0 ]; Deque<Integer> queue = new ArrayDeque <>(); queue.offerLast(0 ); for (int i = 1 ; i < n; i++) { while (queue.peekFirst() < i - k) { queue.pollFirst(); } dp[i] = dp[queue.peekFirst()] + nums[i]; while (!queue.isEmpty() && dp[queue.peekLast()] <= dp[i]) { queue.pollLast(); } queue.offerLast(i); } return dp[n - 1 ]; }
给定一个数组,数组中含有重复的元素,给定两个数字num1,num2,求这两个数字在数组中出现的位置的最小距离。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public static int minDistance (int [] arr,int num1,int num2) { if (arr==null ||arr.length<=0 ) { System.out.println("参数不合格!" ); return Integer.MAX_VALUE; } int lastPos1=-1 ; int lastPos2=-1 ; int minDis=Integer.MAX_VALUE; for (int i=0 ;i<arr.length;++i) { if (arr[i]==num1) { lastPos1=i; if (lastPos2>=0 ) minDis=Math.min(minDis, lastPos1-lastPos2); } if (arr[i]==num2) { lastPos2=i; if (lastPos1>=0 ) minDis=Math.min(minDis, lastPos2-lastPos1); } } return minDis; }
01背包理论基础
对于背包问题,有一种写法, 是使用二维数组,即dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少 。
1 状态转移方程 dp[i][j] = max(dp[i - 1 ][j], dp[i - 1 ][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0 的时候就一定要初始化。
1 2 3 4 5 6 for (int i = 1 ; i < weight.size(); i++) { for (int j = 0 ; j <= bagweight; j++) { if (j < weight[i]) dp[i][j] = dp[i - 1 ][j]; else dp[i][j] = max(dp[i - 1 ][j], dp[i - 1 ][j - weight[i]] + value[i]); } }
1 2 3 4 5 6 7 for (int j = 0 ; j <= bagweight; j++) { for (int i = 1 ; i < weight.size(); i++) { if (j < weight[i]) dp[i][j] = dp[i - 1 ][j]; else dp[i][j] = max(dp[i - 1 ][j], dp[i - 1 ][j - weight[i]] + value[i]); } }
先遍历背包再遍历物品
一维dp数组(滚动数组) 1 2 3 4 5 6 dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); for (int i = 0 ; i < weight.size(); i++) { for (int j = bagWeight; j >= weight[i]; j--) { dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); } }
这里大家发现和二维dp的写法中,遍历背包的顺序是不一样的!
二维dp遍历的时候,背包容量是从小到大,而一维dp遍历的时候,背包是从大到小。
为什么呢?
倒序遍历是为了保证物品i只被放入一次! 。但如果一旦正序遍历了,那么物品0就会被重复加入多次!
再来看看两个嵌套for循环的顺序,代码中是先遍历物品嵌套遍历背包容量,那可不可以先遍历背包容量嵌套遍历物品呢?
不可以!
因为一维dp的写法,背包容量一定是要倒序遍历(原因上面已经讲了),如果遍历背包容量放在上一层,那么每个dp[j]就只会放入一个物品,即:背包里只放入了一个物品。
倒序遍历的原因是,本质上还是一个对二维数组的遍历,并且右下角的值依赖上一层左上角的值,因此需要保证左边的值仍然是上一层的,从右向左覆盖。
完全背包理论基础 每件物品都有无限个(也就是可以放入背包多次) ,求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件 。
而完全背包的物品是可以添加多次的,所以要从小到大去遍历,即:
1 2 3 4 5 6 7 for (int i = 0 ; i < weight.size (); i++) { for (int j = weight[i]; j <= bagWeight ; j++) { dp[j] = max (dp[j], dp[j - weight[i]] + value[i]); } }
在完全背包中,对于一维dp数组来说,其实两个for循环嵌套顺序是无所谓的!
如果求组合数就是外层for循环遍历物品,内层for遍历背包 。
如果求排列数就是外层for遍历背包,内层for循环遍历物品 。
多重背包 很少出现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public int rob (int [] nums) { if (nums.length == 0 ) return 0 ; if (nums.length == 1 ) return nums[0 ]; int result1 = robRange(nums, 0 , nums.length- 2 ); int result2 = robRange(nums, 1 , nums.length - 1 ); return Math.max(result1, result2); } public int robRange (int []nums,int begin, int end) { if (end == begin) return nums[begin]; int [] dp=new int [nums.length]; dp[begin] = nums[begin]; dp[begin + 1 ] = Math.max(nums[begin], nums[begin + 1 ]); for (int i=begin+2 ;i<=end;i++){ dp[i]=Math.max(dp[i-2 ]+nums[i],dp[i-1 ]); } return dp[end]; }
此题破题在于对于负数的处理,选择mindp和maxdp两个来存储最大值、最小值,这样在遇到负数时交换两个的值就可以
139. 单词拆分
dp[i] : 字符串长度为i的话,dp[i]为true,表示可以拆分为一个或多个在字典中出现的单词 。
1 2 3 4 String word=s.substring(j,i); if (set.contains(word)&&dp[j]){ dp[i]=true ; }
494. 目标和
此类型题目一般会给出target 值以及物品值,使用物品值与target匹配在计算dp数组时下标计算则是按照他们target与物品值的差值来计算下标
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 int target = sum / 2 ;int dp[]=new int [target+1 ];for (int i = 0 ; i < n; i++) { for (int j = target; j >=nums[i] ; j--) { dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]); } if (dp[target] == target) return true ; } for (int i = 0 ; i < nums.length; i++) sum += nums[i]; if ( target < 0 && sum < -target) return 0 ; if ((target + sum) % 2 != 0 ) return 0 ; int size = (target + sum) / 2 ; if (size < 0 ) size = -size; int [] dp = new int [size + 1 ]; dp[0 ] = 1 ; for (int i = 0 ; i < nums.length; i++) { for (int j = size; j >= nums[i]; j--) { dp[j] += dp[j - nums[i]]; } } for (int i = 0 ; i < coins.length; i++) { for (int j = coins[i]; j < dp.length; j++) { if (dp[j - coins[i]]!=max){ dp[j]=Math.min(dp[j],dp[j-coins[i]]+1 ); } } }
2维的dp数组使用dp[i][j]分别代表第一个数组和第二个数组的长度 他们在创建时都创建为dp[i+1][j+1]这样才能读取前一个的字符位置计算下一个字符位置,使得字符串长度从1开始而不是从0开始。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 for (int i = 1 ; i <= nums1.size(); i++) { for (int j = 1 ; j <= nums2.size(); j++) { if (nums1[i - 1 ] == nums2[j - 1 ]) { dp[i][j] = dp[i - 1 ][j - 1 ] + 1 ; } if (dp[i][j] > result) result = dp[i][j]; } } for (int i = 1 ; i <=text1.length(); i++) { for (int j = 1 ; j <=text2.length(); j++) { if (text1.charAt(i-1 )==text2.charAt(j-1 )){ dp[i][j]=dp[i-1 ][j-1 ]+1 ; } else { dp[i][j]=Math.max(dp[i-1 ][j],dp[i][j-1 ]); } } int [][] dp = new int [m + 1 ][n + 1 ]; for (int i = 0 ; i <= m; i++) { dp[i][n] = 1 ; } for (int i = m - 1 ; i >= 0 ; i--) { char sChar = s.charAt(i); for (int j = n - 1 ; j >= 0 ; j--) { char tChar = t.charAt(j); if (sChar == tChar) { dp[i][j] = dp[i + 1 ][j + 1 ] + dp[i + 1 ][j]; } else { dp[i][j] = dp[i + 1 ][j]; } } } return dp[0 ][0 ];
这两个就是明显的组合数和排列数的计算,求装满背包有几种方法,递推公式一般都是dp[i] += dp[i - nums[j]];
1 2 3 4 5 6 7 8 9 10 11 12 13 14 for (int i = 0 ; i < coins.size(); i++) { for (int j = coins[i]; j <= amount; j++) { dp[j] += dp[j - coins[i]]; } } for (int i = 0 ; i <= target; i++) { for (int j = 0 ; j < nums.length; j++) { if (i >= nums[j]) { dp[i] += dp[i - nums[j]]; } } }
买卖股票类型题目 121. 买卖股票的最佳时机 ,122. 买卖股票的最佳时机 II ,123. 买卖股票的最佳时机 III ,188. 买卖股票的最佳时机 IV ,309. 买卖股票的最佳时机含冷冻期 ,714. 买卖股票的最佳时机含手续费
对于第一二两个题递推公式为:
这里重申一下dp数组的含义:
- dp[i][0]表示第i天持有股票所得现金。
- dp[i][1] 表示第i天不持有股票所得最多现金
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 第三题 1. 确定dp数组以及下标的含义 一天一共就有五个状态, 1. 没有操作 (其实我们也可以不设置这个状态) 2. 第一次持有股票 3. 第一次不持有股票 4. 第二次持有股票 5. 第二次不持有股票 dp[i][j]中 i表示第i天,j为 [0 - 4] 五个状态,dp[i][j]表示第i天状态j所剩最大现金。 ```java 确定递推公式 达到dp[i][1]状态,有两个具体操作: 操作一:第i天买入股票了,那么dp[i][1] = dp[i-1][0] - prices[i] 操作二:第i天没有操作,而是沿用前一天买入的状态,即:dp[i][1] = dp[i - 1][1] 那么dp[i][1]究竟选 dp[i-1][0] - prices[i],还是dp[i - 1][1]呢? 一定是选最大的,所以 dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][1]); 同理dp[i][2]也有两个操作: 操作一:第i天卖出股票了,那么dp[i][2] = dp[i - 1][1] + prices[i] 操作二:第i天没有操作,沿用前一天卖出股票的状态,即:dp[i][2] = dp[i - 1][2] 所以dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2]) 同理可推出剩下状态部分: dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]); dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]); dp[i][1] = Math.max(dp[i - 1][1], -prices[i]); dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]); dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]); dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
1 2 3 4 5 6 7 8 9 for (int i = 1 ; i < k*2 ; i += 2 ) { dp[0 ][i] = -prices[0 ]; } for (int i = 1 ; i < len; i++) { for (int j = 0 ; j < k*2 - 1 ; j += 2 ) { dp[i][j + 1 ] = Math.max(dp[i - 1 ][j + 1 ], dp[i - 1 ][j] - prices[i]); dp[i][j + 2 ] = Math.max(dp[i - 1 ][j + 2 ], dp[i - 1 ][j + 1 ] + prices[i]); } }
含冷冻期此题
状态一:持有股票状态(今天买入股票,或者是之前就买入了股票然后没有操作,一直持有)
不持有股票状态,这里就有两种卖出股票状态
状态二:保持卖出股票的状态(两天前就卖出了股票,度过一天冷冻期。或者是前一天就是卖出股票状态,一直没操作)
状态三:今天卖出股票
状态四:今天为冷冻期状态,但冷冻期状态不可持续,只有一天!
for (int i = 1; i < n; i++) {
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]));
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];
}
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 手续费题思路和第二题相似只需要在执行时减去手续费 ### 特殊思想dp转换 #### [72. 编辑距离](https://leetcode.cn/problems/edit-distance/) 关键点在于理解转换三个状态其中,`dp[i-1][j-1]` 表示替换操作,`dp[i-1][j]` 表示删除操作,`dp[i][j-1]` 表示插入操作。 ```java // 第一行 for (int j = 1; j <= n2; j++) dp[0][j] = dp[0][j - 1] + 1; // 第一列 for (int i = 1; i <= n1; i++) dp[i][0] = dp[i - 1][0] + 1; for (int i = 1; i <= n1; i++) { for (int j = 1; j <= n2; j++) { if (word1.charAt(i - 1) == word2.charAt(j - 1)) dp[i][j] = dp[i - 1][j - 1]; else dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1; } }
337.打家劫舍 III 树形dp的应用 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public int rob3 (TreeNode root) { int [] res = robAction1(root); return Math.max(res[0 ], res[1 ]); } int [] robAction1(TreeNode root) { int res[] = new int [2 ]; if (root == null ) return res; int [] left = robAction1(root.left); int [] right = robAction1(root.right); res[0 ] = Math.max(left[0 ], left[1 ]) + Math.max(right[0 ], right[1 ]); res[1 ] = root.val + left[0 ] + right[0 ]; return res; }
状态方程很明显
dpi+1 =max(dpi ,dpj +endi −stari +tipi )
基础思想在于及时更新前面地区所取得的费用也就是没此在计算前更新dp[rides[1]]之前的数据,二分优化:找到在第 i 个乘客上车地点之前,最后一个下车地点不大于 starti 的乘客,记为 j.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 public long maxTaxiEarnings (int n, int [][] rides) { long [] dp = new long [n+1 ]; Arrays.sort(rides, (a,b) -> a[1 ]-b[1 ]); int end = 1 ; for (int [] ride:rides) { for (; end <= ride[1 ]; end++) { dp[end] = Math.max(dp[end], dp[end-1 ]); } dp[ride[1 ]] = Math.max(dp[ride[1 ]], dp[ride[0 ]] + ride[2 ] + ride[1 ] - ride[0 ]); } long res = 0 ; for (int i = 0 ; i <= n; i++) { res = Math.max(res, dp[i]); } return res; } public long maxTaxiEarnings (int n, int [][] rides) { Arrays.sort(rides, (a, b) -> a[1 ] - b[1 ]); int m = rides.length; long [] dp = new long [m + 1 ]; for (int i = 0 ; i < m; i++) { int j = binarySearch1(rides, i, rides[i][0 ]); dp[i + 1 ] = Math.max(dp[i], dp[j] + rides[i][1 ] - rides[i][0 ] + rides[i][2 ]); } return dp[m]; } private int binarySearch1 (int [][] rides, int right, int target) { int low = 0 ; while (low<right){ int mid=low+(right-low)/2 ; if (rides[mid][1 ]>target){ right=mid; } else low=mid+1 ; } return low; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public int jobScheduling (int [] startTime, int [] endTime, int [] profit) { int n = startTime.length; int [][] jobs = new int [n][]; for (int i = 0 ; i < n; ++i) jobs[i] = new int []{startTime[i], endTime[i], profit[i]}; Arrays.sort(jobs, (a, b) -> a[1 ] - b[1 ]); int [] f = new int [n + 1 ]; for (int i = 0 ; i < n; ++i) { int j = Search(jobs, i, jobs[i][0 ]); f[i + 1 ] = Math.max(f[i], f[j + 1 ] + jobs[i][2 ]); } return f[n]; } public int Search (int [][] jobs, int right, int target) { int left = 0 ; while (left < right) { int mid = left + (right - left) / 2 ; if (jobs[mid][1 ] > target) { right = mid; } else { left = mid + 1 ; } } return left; }
此题意义就是将图块分割为不同大小的块,计算总价值最大的情况,找到dp公式分三种情况,一直直接卖,一种垂直切割后卖,一种水平切割后卖
1 2 3 4 5 6 7 8 9 10 11 12 13 14 public long sellingWood (int m, int n, int [][] prices) { int [][] pr = new int [m + 1 ][n + 1 ]; for (int p[] : prices) pr[p[0 ]][p[1 ]] = p[2 ]; long [][] f = new long [m + 1 ][n + 1 ]; for (int i = 0 ; i <=m; i++) { for (int j = 0 ; j <=n; j++) { f[i][j]=pr[i][j]; for (int k = 1 ; k < j; k++) f[i][j] = Math.max(f[i][j], f[i][k] + f[i][j - k]); for (int k = 1 ; k < i; k++) f[i][j] = Math.max(f[i][j], f[k][j] + f[i - k][j]); } } return f[m][n]; }
此类面积dp都是以i,j代表矩形或者正方形的右下顶点,dp[i] [j]就可以靠左边上方左上方得到
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public int maximalSquare (char [][] matrix) { int maxSide = 0 ; if (matrix == null || matrix.length == 0 || matrix[0 ].length == 0 ) { return maxSide; } int rows = matrix.length, columns = matrix[0 ].length; int [][] dp = new int [rows][columns]; for (int i = 0 ; i < rows; i++) { for (int j = 0 ; j < columns; j++) { if (matrix[i][j] == '1' ) { if (i == 0 || j == 0 ) { dp[i][j] = 1 ; } else { dp[i][j] = Math.min(Math.min(dp[i - 1 ][j], dp[i][j - 1 ]), dp[i - 1 ][j - 1 ]) + 1 ; } maxSide = Math.max(maxSide, dp[i][j]); } } } int maxSquare = maxSide * maxSide; return maxSquare; }
记忆化搜索
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public int findRotateSteps (String ring, String key) { int r=ring.length(),k=key.length(); List<Integer>pos[]=new List [26 ]; for (int i = 0 ; i < 26 ; ++i) { pos[i] = new ArrayList <Integer>(); } for (int i = 0 ; i < r; i++) { pos[ring.charAt(i)-'a' ].add(i); } int dp[][]=new int [k][r]; for (int i = 0 ; i <k ; i++) { Arrays.fill(dp[i], 0x3f3f3f ); } for (int i : pos[key.charAt(0 ) - 'a' ]) { dp[0 ][i] = Math.min(i, r - i) + 1 ; } for (int i = 1 ; i < k; i++) { for (int j :pos[key.charAt(i)-'a' ]) { for (int l:pos[key.charAt(i-1 )-'a' ]) { dp[i][j]=Math.min(dp[i][j],dp[i-1 ][l]+ Math.min(Math.abs(j - l), r - Math.abs(j - l)) + 1 ); } } } return Arrays.stream(dp[k - 1 ]).min().getAsInt(); }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public int stoneGameVII (int [] stones) { int n=stones.length; int sum[]=new int [n+1 ]; int momo[][]=new int [n][n]; for (int i = 1 ; i < sum.length; i++) { sum[i]+=sum[i-1 ]+stones[i-1 ]; } int res=dfs(0 ,n-1 ,sum,momo); return res; } public int dfs (int begin,int end , int sum[],int mono[][]) { if (begin==end)return 0 ; if (mono[begin][end]>0 )return mono[begin][end]; int res1=sum[end+1 ]-sum[begin+1 ]-dfs(begin+1 ,end,sum,mono); int res2=sum[end]-sum[begin]-dfs(begin,end-1 ,sum,mono); return mono[begin][end]=Math.max(res1,res2); }
这两个题都是动态规划,使用dp[i] [j]二维数组储存代表字符串从i 到j 的的最少插入次数/最长子序列, 然后从数组尾部开始遍历,直到遍历完整个数组为止
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 public int minInsertions (String s) { int n = s.length(); int [][]dp=new int [n][n]; for (int i=n-1 ;i>=0 ;i--){ for (int j=i+1 ;j<n;j++){ if (s.charAt(i)==s.charAt(j)){ dp[i][j]=dp[i+1 ][j-1 ]; } else { dp[i][j]=Math.min(dp[i+1 ][j],dp[i][j-1 ])+1 ; } } } return dp[0 ][n-1 ]; } public int longestPalindromeSubseq (String s) { int [][]dp=new int [s.length()][s.length()]; for (int i = 0 ; i < s.length(); i++) dp[i][i] = 1 ; for (int i=s.length()-1 ;i>=0 ;i--) { for (int j=i+1 ;j<s.length();j++){ if (s.charAt(i)==s.charAt(j)){ dp[i][j]=dp[i+1 ][j-1 ]+2 ; } else { dp[i][j]=Math.max(dp[i+1 ][j],dp[i][j-1 ]); } } } return dp[0 ][s.length()-1 ]; }
单调栈 如何移除最大的数字首先是贪心算法计算左边数字和右边数字的大小,如果左边小就不移除保留,如果右边小于左边就移除左边
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public String removeKdigits (String num, int k) { Deque<Character> deque = new LinkedList <Character>(); int length = num.length(); for (int i = 0 ; i < length; ++i) { char digit = num.charAt(i); while (!deque.isEmpty() && k > 0 && deque.peekLast() > digit) { deque.pollLast(); k--; } deque.offerLast(digit); } for (int i = 0 ; i < k; ++i) { deque.pollLast(); } StringBuilder ret = new StringBuilder (); boolean leadingZero = true ; while (!deque.isEmpty()) { char digit = deque.pollFirst(); if (leadingZero && digit == '0' ) { continue ; } leadingZero = false ; ret.append(digit); } return ret.length() == 0 ? "0" : ret.toString(); }
这题基本思路也是使用比较将之前放入栈的元素给弹出,但是作为判断方法这个使用的是出现的总频率(int[] num = new int[26];)来选择再来根据大小判断是否弹出,
boolean[] vis = new boolean[26];则是保证每个字母都被用到,这样就可以得到最小的字母顺序组
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public String removeDuplicateLetters (String s) { boolean [] vis = new boolean [26 ]; int [] num = new int [26 ]; for (int i = 0 ; i < s.length(); i++) { num[s.charAt(i) - 'a' ]++; } StringBuffer sb = new StringBuffer (); for (int i = 0 ; i < s.length(); i++) { char ch = s.charAt(i); if (!vis[ch - 'a' ]) { while (sb.length() > 0 && sb.charAt(sb.length() - 1 ) > ch) { if (num[sb.charAt(sb.length() - 1 ) - 'a' ] > 0 ) { vis[sb.charAt(sb.length() - 1 ) - 'a' ] = false ; sb.deleteCharAt(sb.length() - 1 ); } else { break ; } } vis[ch - 'a' ] = true ; sb.append(ch); } num[ch - 'a' ] -= 1 ; } return sb.toString(); }
使用哨兵加单调栈的思想,分别先求每个元素左边最小元素的位置,然后再求右边的最小元素的位置
我们用一个具体的例子[6,7,5,2,4,5,9,3] 来帮助读者理解单调栈。我们需要求出每一根柱子的左侧且最近的小于其高度的柱子。初始时的栈为空。
我们枚举 6,因为栈为空,所以 6 左侧的柱子是「哨兵」,位置为 -1。随后我们将 6 入栈。
栈:[6(0)]。(这里括号内的数字表示柱子在原数组中的位置)
栈:[6(0), 7(1)]
栈:[5(2)]
栈:[2(3)]
栈:[2(3), 4(4), 5(5), 9(6)]
栈:[2(3), 3(7)]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public int largestRectangleArea (int [] heights) { int n = heights.length; int [] left = new int [n]; int [] right = new int [n]; Arrays.fill(right, n); Deque<Integer> stack = new ArrayDeque <Integer>(); for (int i = 0 ; i < heights.length; i++) { while (!stack.isEmpty()&&heights[stack.peek()]>=heights[i]){ right[stack.peek()] = i; stack.pop(); } left[i]=(stack.isEmpty() ? -1 : stack.peek()); stack.push(i); } int res=0 ; for (int i = 0 ; i < heights.length; i++) { res=Math.max(res,(right[i]-left[i]-1 )*heights[i]); } return res; }
84题的变形应用,枚举矩阵高度从1开始一直到n这样就将此题转换为84题求最大矩形的问题
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 public int maximalRectangle (char [][] matrix) { if (matrix.length == 0 ) { return 0 ; } int [] heights = new int [matrix[0 ].length]; int maxArea = 0 ; for (int row = 0 ; row < matrix.length; row++) { for (int col = 0 ; col < matrix[0 ].length; col++) { if (matrix[row][col] == '1' ) { heights[col] += 1 ; } else { heights[col] = 0 ; } } maxArea = Math.max(maxArea, largestRectangleArea(heights)); } return maxArea; } public int largestRectangleArea (int [] heights) { int maxArea = 0 ; Stack<Integer> stack = new Stack <>(); int p = 0 ; while (p < heights.length) { if (stack.isEmpty()) { stack.push(p); p++; } else { int top = stack.peek(); if (heights[p] >= heights[top]) { stack.push(p); p++; } else { int height = heights[stack.pop()]; int leftLessMin = stack.isEmpty() ? -1 : stack.peek(); int RightLessMin = p; int area = (RightLessMin - leftLessMin - 1 ) * height; maxArea = Math.max(area, maxArea); } } } while (!stack.isEmpty()) { int height = heights[stack.pop()]; int leftLessMin = stack.isEmpty() ? -1 : stack.peek(); int RightLessMin = heights.length; int area = (RightLessMin - leftLessMin - 1 ) * height; maxArea = Math.max(area, maxArea); } return maxArea; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public int [] secondGreaterElement(int [] nums) { int n = nums.length; int [] res = new int [n]; Arrays.fill(res, -1 ); List<Integer> stack1 = new ArrayList <Integer>(); List<Integer> stack2 = new ArrayList <Integer>(); for (int i = 0 ; i < n; ++i) { int v = nums[i]; while (!stack2.isEmpty() && nums[stack2.get(stack2.size() - 1 )] < v) { res[stack2.get(stack2.size() - 1 )] = v; stack2.remove(stack2.size() - 1 ); } int pos = stack1.size() - 1 ; while (pos >= 0 && nums[stack1.get(pos)] < v) { --pos; } for (int j = pos + 1 ; j < stack1.size(); j++) { stack2.add(stack1.get(j)); } for (int j = stack1.size() - 1 ; j >= pos + 1 ; j--) { stack1.remove(j); } stack1.add(i); } return res; }
寻找到左边非递增的数和右边非递增的数,我们使用前后两个方向数组去存储前后缀和
对于左侧的非递减:将 maxHeights 依次入栈,对于第 i 个元素来说,不断从栈顶弹出元素,直到栈顶元素小于等于 **maxHeights[i]**。假设此时栈顶元素为 **maxHeights[j]**,则区间[j+1,i−1] 中的元素最多只能取到 **maxHeights[i],则 prefix[i]=prefix[j]+(i−j)×maxHeights[i]**;
对于右侧的非递减:将 maxHeights 依次入栈,对于第 i 个元素来说,不断从栈顶弹出元素,直到栈顶元素小于等于 **maxHeights[i]**。假设此时栈顶元素为 **maxHeights[j]**,则区间 [i+1,j−1] 中的元素最多只能取到 **maxHeights[i]**,则 suffix[i]=suffix[j]+(j−i)×maxHeights[i];
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 public long maximumSumOfHeights (List<Integer> maxHeights) { int n = maxHeights.size(); long res = 0 ; long [] prefix = new long [n]; long [] suffix = new long [n]; Deque<Integer> stack1 = new ArrayDeque <Integer>(); Deque<Integer> stack2 = new ArrayDeque <Integer>(); for (int i = 0 ; i < n; i++) { while (!stack1.isEmpty() && maxHeights.get(i) < maxHeights.get(stack1.peek())) { stack1.pop(); } if (stack1.isEmpty()) { prefix[i] = (long ) (i + 1 ) * maxHeights.get(i); } else { prefix[i] = prefix[stack1.peek()] + (long ) (i - stack1.peek()) * maxHeights.get(i); } stack1.push(i); } for (int i = n - 1 ; i >= 0 ; i--) { while (!stack2.isEmpty() && maxHeights.get(i) < maxHeights.get(stack2.peek())) { stack2.pop(); } if (stack2.isEmpty()) { suffix[i] = (long ) (n - i) * maxHeights.get(i); } else { suffix[i] = suffix[stack2.peek()] + (long ) (stack2.peek() - i) * maxHeights.get(i); } stack2.push(i); res = Math.max(res, prefix[i] + suffix[i] - maxHeights.get(i)); } return res; }
并查集 首先要知道并查集可以解决什么问题呢? 主要就是集合问题,两个节点在不在一个集合,也可以将两个节点添加到一个集合中。
这里整理出我的并查集模板如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 int n = 1005 ; int father[1005 ];void init () for (int i = 0 ; i < n; ++i) { father[i] = i; } } int find (int u) return u == father[u] ? u : father[u] = find (father[u]); } void join (int u, int v) u = find (u); v = find (v); if (u == v) return ; father[v] = u; } bool same (int u, int v) u = find (u); v = find (v); return u == v; }
寻找根节点,函数:find(int u),也就是判断这个节点的祖先节点是哪个
将两个节点接入到同一个集合,函数:join(int u, int v),将两个节点连在同一个根节点上
判断两个节点是否在同一个集合,函数:same(int u, int v),就是判断两个节点是不是同一个根节点
存储数据结构 如何表示节点与节点之间的连通性关系呢??
用数组parent[]来表示这种关系
如果自己就是根节点,那么parent[i] = i,即自己指向自己
如果自己不是根节点,则parent[i] = root id
1 2 3 4 5 6 7 8 9 10 11 private int count;private int [] parent;public UF (int n) { this .count = n; parent = new int [n]; for (int i = 0 ; i < n; i++) { parent[i] = i; } }
优化角度 1:平衡性优化 思路:当我们每次连接两个节点的时候,不希望出现头重脚轻的情况,而希望到达一种平衡的状态
使用额外的一个数组size[]记录每个连通分量中的节点数,每次均把节点数少的分量接到节点数多的分量上,如图
注意:只有每个连通分量的根节点的 size[] 才可以代表该连通分量中的节点数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 private int count;private int [] parent;private int [] size;public UF (int n) { this .count = n; parent = new int [n]; size = new int [n]; for (int i = 0 ; i < n; i++) { parent[i] = i; size[i] = 1 ; } } public void union (int p, int q) { int rootP = find(p); int rootQ = find(q); if (rootP == rootQ) return ; if (size[rootP] < size[rootQ]) { parent[rootP] = rootQ; size[rootQ] += size[rootP] } else { parent[rootQ] = rootP; size[rootP] += size[rootQ] } count--; }
优化角度 2:路径压缩 思路:使树高始终保持为常数
1 2 3 4 5 6 7 8 private int find(int x) { while (parent[x] != x) { // 进行路径压缩 parent[x] = parent[parent[x]]; x = parent[x]; } return x; }
上面是用迭代实现的「路径压缩」,下面给出一种用递归实现的「路径压缩」,其效率更高!
1 2 3 4 5 6 private int find (int x) { if (parent[x] != x) { parent[x] = find(parent[x]); } return parent[x]; }
递归直接一次性把一棵树拉平了!!**(强力推荐使用这种方法!!!✨✨✨)**
注意:
「路径压缩优化」比「平衡性优化」更为常用
当使用了「路径压缩优化」后,「平衡性优化」可以不使用
但是可以在某些题目中使用「平衡性优化」的思想,如 最长连续序列
完整模版 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 class UF { private int count; private int [] parent; private int [] size; public UF (int n) { this .count = n; parent = new int [n]; size = new int [n]; for (int i = 0 ; i < n; i++) { parent[i] = i; size[i] = 1 ; } } public void union (int p, int q) { int rootP = find(p); int rootQ = find(q); if (rootP == rootQ) return ; if (size[rootP] < size[rootQ]) { parent[rootP] = rootQ; size[rootQ] += size[rootP]; } else { parent[rootQ] = rootP; size[rootP] += size[rootQ]; } this .count--; } public boolean connected (int p, int q) { int rootP = find(p); int rootQ = find(q); return rootP == rootQ; } public int count () { return this .count; } private int find (int x) { if (parent[x] != x) { parent[x] = find(parent[x]); } return parent[x]; } }
1.读取[1,2]:
2.读取[3, 4]
3.读取[3, 2]
4.最后读取[1,4].判断重复
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public int [] findRedundantConnection(int [][] edges) { int n = edges.length; int [] parent = new int [n + 1 ]; for (int i = 1 ; i <= n; i++) { parent[i] = i; } for (int i = 0 ; i < n; i++) { int edge[]=edges[i]; int node1 = edge[0 ], node2 = edge[1 ]; if (find(parent,node1)!=find(parent,node2)){ union(parent,node1,node2); }else { return edge; } } return new int [0 ]; } public void union (int [] parent, int index1, int index2) { parent[find(parent,index1)]=find(parent,index2); } public int find (int [] parent, int index) { if (parent[index] != index) { parent[index] = find(parent, parent[index]); } return parent[index]; }
看到最短首先想到的就是广度优先搜索
标准转化为并查集题目 将两个节点的相等和不等性转换为并查集
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 public boolean equationsPossible (String[] equations) { int parent[]=new int [26 ]; for (int i = 0 ; i < parent.length; i++) { parent[i]=i; } for (String str : equations) { if (str.charAt(1 ) == '=' ) { int index1 = str.charAt(0 ) - 'a' ; int index2 = str.charAt(3 ) - 'a' ; union(parent, index1, index2); } } for (String str : equations) { if (str.charAt(1 ) == '!' ) { int index1 = str.charAt(0 ) - 'a' ; int index2 = str.charAt(3 ) - 'a' ; if (find(parent, index1) == find(parent, index2)) { return false ; } } } return true ; } public int find (int parent[],int x) { if (parent[x]!=x){ parent[x]=find(parent,parent[x]); } return parent[x]; } public void union (int parent[],int x,int y) { int rootX=find(parent,x); int rootY=find(parent,y); parent[rootX]=rootY; }
根据 a 经过 b 可以到达 c,a 经过 d 也可以到达 c,因此 两条路径上的有向边的权值的乘积是一定相等的。设 b 到 c 的权值为 xxx,那么 3.0⋅x=6.0⋅4.0,得 x=8.0。
一边查询一边修改结点指向是并查集的特色。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 public double [] calcEquation(List<List<String>> equations, double [] values, List<List<String>> queries) { int equationsSize = equations.size(); UnionFind unionFind = new UnionFind (2 * equationsSize); Map<String, Integer> hashMap = new HashMap <>(2 * equationsSize); int id = 0 ; for (int i = 0 ; i < equationsSize; i++) { List<String> equation = equations.get(i); String var1 = equation.get(0 ); String var2 = equation.get(1 ); if (!hashMap.containsKey(var1)) { hashMap.put(var1, id); id++; } if (!hashMap.containsKey(var2)) { hashMap.put(var2, id); id++; } unionFind.union(hashMap.get(var1), hashMap.get(var2), values[i]); } int queriesSize = queries.size(); double [] res = new double [queriesSize]; for (int i = 0 ; i < queriesSize; i++) { String var1 = queries.get(i).get(0 ); String var2 = queries.get(i).get(1 ); Integer id1 = hashMap.get(var1); Integer id2 = hashMap.get(var2); if (id1 == null || id2 == null ) { res[i] = -1.0d ; } else { res[i] = unionFind.isConnected(id1, id2); } } return res; } private class UnionFind { private int parent[]; private double weight[]; public UnionFind (int n) { this .parent=new int [n]; this .weight=new double [n]; for (int i = 0 ; i < n; i++) { parent[i]=i; weight[i]=1.0d ; } } public void union (int x, int y, double value) { int rootX = find(x); int rootY = find(y); if (rootY==rootX)return ; parent[rootX]=rootY; weight[rootX]=weight[y]*value/weight[x]; } public int find (int x) { if (parent[x]!=x){ int origin = parent[x]; parent[x] = find(parent[x]); weight[x] *= weight[origin]; } return parent[x]; } public double isConnected (int x, int y) { int rootX = find(x); int rootY = find(y); if (rootX == rootY) { return weight[x] / weight[y]; } else { return -1.0d ; } } }
位运算 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 private int cntInt (int val) { int count = 0 ; while (val > 0 ) { val = val & (val - 1 ); count ++; } return count; } public int [] sortByBits(int [] arr) { return Arrays.stream(arr).boxed() .sorted(new Comparator <Integer>(){ @Override public int compare (Integer o1, Integer o2) { int cnt1 = cntInt(o1); int cnt2 = cntInt(o2); return (cnt1 == cnt2) ? Integer.compare(o1, o2) : Integer.compare(cnt1, cnt2); } }) .mapToInt(Integer::intValue) .toArray(); }
这段代码的作用是对一个 int 数组进行排序,排序规则是首先按照每个数的数字个数从小到大排序,如果数字个数相同,则按照数值大小从小到大排序。
具体实现是通过使用 Java 8 中的流式 API,将 int 数组转换为一个 IntStream 流,并对流中的元素进行操作。代码首先使用 boxed() 方法将流中的元素转换为 Integer 对象,然后使用 sorted() 方法对这些 Integer 对象进行排序。
sorted() 方法接受一个 Comparator 对象作为参数,这里创建了一个匿名的 Comparator 对象来实现自定义的排序规则。在 compare() 方法中,首先分别计算了两个数字的数字个数,然后根据这些数字个数进行比较。如果数字个数相同,则按照数值大小进行比较,使用 Integer.compare() 方法进行比较。最后,使用 mapToInt() 方法将排序后的 Integer 对象转换为 int 类型的流,并使用 toArray() 方法将其转换为一个 int 数组,即返回排序后的结果。
需要注意的是,该实现对每个数都会计算一遍数字个数,因此在对大量数据进行排序时可能会影响性能。如果要优化性能,可以考虑使用缓存来避免重复计算数字个数。
官解写的太复杂了,其实就是我们只看第一个二进制位,只存在0,1两种情况,所以如果left<right,区间中必然存在left+1,那么最低位&一下一定等于0了,然后不停的右移,一直移到两个相等为止,就这么简单
1 2 3 4 5 6 7 8 9 10 public int rangeBitwiseAnd (int m, int n) { int shift = 0 ; while (m < n) { m >>= 1 ; n >>= 1 ; ++shift; } return m << shift; }
贪心算法 贪心顾名思义,就是满足每步解的最优解,这样最终解就是最优解
主要思想为计算每一步能够跳到的最大值,然后一直到最后返回true或者返回计算步数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 for (int i=0 ;i<=cover;i++){ cover = Math.max(i + nums[i], cover); if (cover>=nums.length-1 ) return true ; } return false ; for (int i = 0 ; i < nums.length-1 ; i++) { max=Math.max(max,i+nums[i]); if (i==end) { end = max; res++; } }
关键思路:要能够正常启动首先gas[i]-cost[i]>=0,其次就是能否走完最终路程需要看gas和与cost和大小如果大于那么就可以走完
1 2 3 4 5 6 7 8 for (int i=0 ;i<gas.length;i++){ curSum+=gas[i]-cost[i]; TotalSum+=gas[i]-cost[i]; if (curSum<0 ){ start=i+1 ; curSum=0 ; } }
注意下标和存储的结合
1 2 3 4 5 6 7 8 9 10 11 12 13 14 for (int i : hand) { map.put(i, map.getOrDefault(i, 0 ) + 1 ); q.add(i); } while (!q.isEmpty()) { int t = q.poll(); if (map.get(t) == 0 ) continue ; for (int i = 0 ; i < groupSize; i++) { int cnt = map.getOrDefault(t + i, 0 ); if (cnt == 0 ) return false ; map.put(t + i, cnt - 1 ); } } return true ;
关键在于满足每个三元组的要求 ,也就是每个三元组的每个位置数值满足小于等于,指定位数值相等
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 for (int i = 0 ; i < triplets.length; i++) { if (triplets[i][0 ]==target[0 ] && triplets[i][1 ]<=target[1 ] && triplets[i][2 ]<=target[2 ]){ one=true ; } if (triplets[i][0 ]<=target[0 ] && triplets[i][1 ]==target[1 ] && triplets[i][2 ]<=target[2 ]){ two=true ; } if (triplets[i][0 ]<=target[0 ] && triplets[i][1 ]<=target[1 ] && triplets[i][2 ]==target[2 ]){ three=true ; } if (one && three && two){ return true ; } } return false ;
使用元素最后一次出现的位置作为最大值,找到最大的切割位置,在这个位置内的元素最大出现的位置都不会大于最大位置
1 2 3 4 5 6 7 8 9 10 11 12 13 14 int last[]=new int [26 ]; int length = s.length(); for (int i = 0 ; i < length; i++) { last[s.charAt(i) - 'a' ] = i; } List<Integer> partition = new ArrayList <Integer>(); int start = 0 , end = 0 ; for (int i = 0 ; i < length; i++) { end = Math.max(end, last[s.charAt(i) - 'a' ]); if (i == end) { partition.add(end - start + 1 ); start = end + 1 ; } }
我们从后往前倒序遍历一次数组,依次比较两个相邻的元素,如果两个相邻的元素能够合并,就将其合并。如果不能合并,就继续往前判断。因为这样的操作流程,在比较过程中,靠后的数是所有操作流程可能性中能产生的最大值,而靠前的数,是所有操作流程可能性中能产生的最小值。如果在遍历过程中,比较的结果是不能合并,那么其他任何操作流程都无法合并这两个数。如果可以合并,那我们就贪心地合并,因为这样能使接下来的比较中,靠后的数字尽可能大。
1 2 3 4 5 6 7 public long maxArrayValue (int [] nums) { long sum = nums[nums.length - 1 ]; for (int i = nums.length - 2 ; i >= 0 ; i--) { sum = nums[i] <= sum ? nums[i] + sum : nums[i]; } return sum; }
621. 任务调度器
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 public int leastInterval (char [] tasks, int n) { int [] hash = new int [26 ]; for (int i = 0 ; i < tasks.length; ++i) { hash[tasks[i] - 'A' ] += 1 ; } Arrays.sort(hash); int minLen = (n+1 ) * (hash[25 ] - 1 ) + 1 ; for (int i = 24 ; i >= 0 ; --i){ if (hash[i] == hash[25 ]) ++ minLen; } return Math.max(minLen, tasks.length); }
Intervals 插空类题目 栈的思想使用左栈和*号栈存储
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 Deque<Integer> leftStack = new LinkedList <Integer>(); Deque<Integer> asteriskStack = new LinkedList <Integer>(); int n = s.length();for (int i = 0 ; i < n; i++) { char c = s.charAt(i); if (c == '(' ) { leftStack.push(i); } else if (c == '*' ) { asteriskStack.push(i); } else { if (!leftStack.isEmpty()) { leftStack.pop(); } else if (!asteriskStack.isEmpty()) { asteriskStack.pop(); } else { return false ; } } } while (!leftStack.isEmpty() && !asteriskStack.isEmpty()) { int leftIndex = leftStack.pop(); int asteriskIndex = asteriskStack.pop(); if (leftIndex > asteriskIndex) { return false ; } } return leftStack.isEmpty();
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public int [][] merge(int [][] intervals) { List<int []> res = new LinkedList <>(); Arrays.sort(intervals,(a,b)->Integer.compare(a[0 ],b[0 ])); int left=intervals[0 ][0 ]; int right=intervals[0 ][1 ]; for (int i=1 ;i<intervals.length;i++){ if (intervals[i][0 ]>right){ res.add(new int []{left, right}); left = intervals[i][0 ]; right = intervals[i][1 ]; } else { right=Math.max(intervals[i][1 ],right); } } res.add(new int []{left, right}); return res.toArray(new int [res.size()][]); }
贪心思想,先将数组按照结尾排序,然后每次找到相交数组的最小结束长度,分割,这样最后总数组数减去分割出的不相交的数组个数就得到了需要删除的数组个数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public int eraseOverlapIntervals (int [][] intervals) { if (intervals.length == 0 ) { return 0 ; } Arrays.sort(intervals,new Comparator <int []>(){ @Override public int compare (int [] o1, int [] o2) { return o1[1 ]-o2[1 ]; } }); int n = intervals.length; int right=intervals[0 ][1 ]; int ans=1 ; for (int i = 1 ; i < n; i++) { if (intervals[i][0 ]>=right){ ans++; right=intervals[i][1 ]; } } return n-ans; }
扫描线 将每个矩形 rectangles[i] 看做两条竖直方向的边,使用 (x,y1,y2) 的形式进行存储(其中 y1 代表该竖边的下端点,y2 代表竖边的上端点),同时为了区分是矩形的左边还是右边,再引入一个标识位,即以四元组 (x,y1,y2,flag) 的形式进行存储。
一个完美矩形的充要条件为:对于完美矩形的每一条非边缘的竖边,都「成对」出现(存在两条完全相同的左边和右边重叠在一起);对于完美矩形的两条边缘竖边,均独立为一条连续的(不重叠)的竖边。
如图(红色框的为「完美矩形的边缘竖边」,绿框的为「完美矩形的非边缘竖边」):
此题第一眼思路是暴力求解,但是细想后发现可以先排序intervals和queries 这样遍历时就不需要每次把intervals全遍历只要遍历到intervals[i][1]<queries就可以(离线算法 是指在开始时就需要知道问题的所有输入数据,而且在解决一个问题后就要立即输出结果)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public int [] minInterval(int [][] intervals, int [] queries) { Integer[] qindex = new Integer [queries.length]; for (int i = 0 ; i < queries.length; i++) { qindex[i] = i; } Arrays.sort(qindex, (i, j) -> queries[i] - queries[j]); Arrays.sort(intervals, (i, j) -> i[0 ] - j[0 ]); PriorityQueue<int []> pq = new PriorityQueue <int []>((a, b) -> a[0 ] - b[0 ]); int [] res = new int [queries.length]; Arrays.fill(res, -1 ); int i = 0 ; for (int qi : qindex) { while (i < intervals.length && intervals[i][0 ] <= queries[qi]) { pq.offer(new int []{intervals[i][1 ] - intervals[i][0 ] + 1 , intervals[i][0 ], intervals[i][1 ]}); i++; } while (!pq.isEmpty() && pq.peek()[2 ] < queries[qi]) { pq.poll(); } if (!pq.isEmpty()) { res[qi] = pq.peek()[0 ]; } } return res; }
会议室经典题 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 public boolean canAttendMeetings (List<Interval> intervals) { Collections.sort(intervals, (a, b) -> a.start - b.start); for (int i = 1 ; i < intervals.size(); i++) { if (intervals.get(i - 1 ).end > intervals.get(i).start) { return false ; } } return true ; } public int minMeetingRooms (List<Interval> intervals) { if (intervals.size() == 0 ) { return 0 ; } Integer[] start = new Integer [intervals.size()]; Integer[] end = new Integer [intervals.size()]; for (int i = 0 ; i < intervals.size(); i++) { start[i] = intervals.get(i).start; end[i] = intervals.get(i).end; } Arrays.sort( end, new Comparator <Integer>() { public int compare (Integer a, Integer b) { return a - b; } }); Arrays.sort( start, new Comparator <Integer>() { public int compare (Integer a, Integer b) { return a - b; } }); int startPointer = 0 , endPointer = 0 ; int usedRooms = 0 ; while (startPointer < intervals.size()) { if (start[startPointer] >= end[endPointer]) { usedRooms -= 1 ; endPointer += 1 ; } usedRooms += 1 ; startPointer += 1 ; } return usedRooms; }
数学 快速幂 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 (a + b) % p = (a % p + b % p) % p (1 ) (a - b) % p = (a % p - b % p ) % p (2 ) (a * b) % p = (a % p * b % p) % p (3 ) a ^ b % p = ((a % p)^b) % p (4 ) long c=10000007 ;public long divide (long a, long b) { if (b == 0 ) return 1 ; else if (b % 2 == 0 ) return divide((a % c) * (a % c), b / 2 ) % c; else return a % c * divide((a % c) * (a % c), (b - 1 ) / 2 ) % c; } long c = 1000000007 ;public long divide (long a, long b) { a %= c; long res = 1 ; for (; b != 0 ; b /= 2 ) { if (b % 2 == 1 ) res = (res * a) % c; a = (a * a) % c; } return res; } long long int quik_power (int base, int power) { long long int result = 1 ; while (power > 0 ) { if (power & 1 ) result *= base; power >>= 1 ; base *= base; } return result; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 long long int quik_power (int base, int power) { long long int result = 1 ; while (power > 0 ) { if (power & 1 ) result *= base; base *= base; power >>= 1 ; } return result; } long long int quik_power (int base, int power) { long long int result = 1 ; while (power > 0 ) { if (power % 2 == 1 ) result *= base; power /= 2 ; base *= base; } return result; } long long int quik_power (int base, int power) { long long int result = 1 ; while (power > 0 ) { if (power & 1 ) result *= base; power >>= 1 ; base *= base; } return result; }
矩阵快速幂
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution { int N = 3 ; int [][] mul(int [][] a, int [][] b) { int [][] c = new int [N][N]; for (int i = 0 ; i < N; i++) { for (int j = 0 ; j < N; j++) { c[i][j] = a[i][0 ] * b[0 ][j] + a[i][1 ] * b[1 ][j] + a[i][2 ] * b[2 ][j]; } } return c; } public int tribonacci (int n) { if (n == 0 ) return 0 ; if (n == 1 || n == 2 ) return 1 ; int [][] ans = new int [][]{ {1 ,0 ,0 }, {0 ,1 ,0 }, {0 ,0 ,1 } }; int [][] mat = new int [][]{ {1 ,1 ,1 }, {1 ,0 ,0 }, {0 ,1 ,0 } }; int k = n - 2 ; while (k != 0 ) { if ((k & 1 ) != 0 ) ans = mul(ans, mat); mat = mul(mat, mat); k >>= 1 ; } return ans[0 ][0 ] + ans[0 ][1 ]; } }
摩尔投票法:求的是绝对众数(数组总出现频率超过1/2的数)
1 2 3 4 5 6 7 8 public int majorityElement (int [] nums) { int x=0 ,vote=0 ; for (int i = 0 ; i < nums.length; i++) { if (vote==0 )x=nums[i]; vote+=nums[i]==x?1 :-1 ; } return x; }
数组中出现次数超过一半的数字 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public int MoreThanHalfNum_Solution (int [] nums) { int majority = nums[0 ]; for (int i = 1 , cnt = 1 ; i < nums.length; i++) { cnt = nums[i] == majority ? cnt + 1 : cnt - 1 ; if (cnt == 0 ) { majority = nums[i]; cnt = 1 ; } } int cnt = 0 ; for (int val : nums) if (val == majority) cnt++; return cnt > nums.length / 2 ? majority : 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 public int romanToInt (String s) { int sum = 0 ; int preNum = getValue(s.charAt(0 )); for (int i = 1 ;i < s.length(); i ++) { int num = getValue(s.charAt(i)); if (preNum < num) { sum -= preNum; } else { sum += preNum; } preNum = num; } sum += preNum; return sum; } private int getValue (char ch) { switch (ch) { case 'I' : return 1 ; case 'V' : return 5 ; case 'X' : return 10 ; case 'L' : return 50 ; case 'C' : return 100 ; case 'D' : return 500 ; case 'M' : return 1000 ; default : return 0 ; } }
贝祖定理 寻找最大公约数如果target能整除则可以
这样可以化解爆int的情况 提前取模这样余数就不会超int
1 2 3 4 5 6 7 8 9 10 11 12 public int [] divisibilityArray(String word, int m) { int res[]=new int [word.length()]; long cur=0 ; for (int i = 0 ; i < word.length(); i++) { char c=word.charAt(i); cur=cur*10 +Integer.valueOf(i); System.out.println(cur); if (cur%m==0 )res[i]=1 ; else res[i]=0 ; } return res; }
公式!!! 卡塔兰数
1 2 3 4 5 6 7 8 9 10 11 public int numTrees (int n) {int [] dp = new int [n + 1 ]; dp[0 ] = 1 ; dp[1 ] = 1 ; for (int i = 2 ; i <= n; i++) { for (int j = 1 ; j <= i; j++) { dp[i] += dp[j - 1 ] * dp[i - j]; } } return dp[n]; }
随机数生成 470. 用 Rand7() 实现 Rand10()
概念一
已知 rand_N() 可以等概率的生成[1, N]范围的随机数
概念二
只要rand_N()中N是2的倍数,就都可以用来实现rand2(),反之,若N不是2的倍数,则产生的结果不是等概率的
ok,现在回到本题中。已知rand7(),要求通过rand7()来实现rand10()。
有了前面的分析,要实现rand10(),就需要先实现rand_N(),并且保证N大于10且是10的倍数。这样再通过rand_N() % 10 + 1 就可以得到[1,10]范围的随机数了。
]但是这样实现的N不是10的倍数啊!这该怎么处理?这里就涉及到了“拒绝采样”的知识了,也就是说,如果某个采样结果不在要求的范围内,则丢弃它。基于上面的这些分析,再回头看下面的代码,想必是不难理解了。
1 2 3 4 5 6 7 8 class Solution extends SolBase { public int rand10 () { while (true ) { int num = (rand7() - 1 ) * 7 + rand7(); if (num <= 40 ) return num % 10 + 1 ; } } }
根据part 1的分析,我们已经知道(rand7() - 1) * 7 + rand7() 等概率生成[1,49]范围的随机数。而由于我们需要的是10的倍数,因此,不得不舍弃掉[41, 49]这9个数。优化的点就始于——我们能否利用这些范围外的数字,以减少丢弃的值,提高命中率总而提高随机数生成效率。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution extends SolBase { public int rand10 () { while (true ) { int a = rand7(); int b = rand7(); int num = (a-1 )*7 + b; if (num <= 40 ) return num % 10 + 1 ; a = num - 40 ; b = rand7(); num = (a-1 )*7 + b; if (num <= 60 ) return num % 10 + 1 ; a = num - 60 ; b = rand7(); num = (a-1 )*7 + b; if (num <= 20 ) return num % 10 + 1 ; } } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public int findKthNumber (int n, int k) { int ans = 1 ; while (k > 1 ) { int cnt = getCnt(ans, n); if (cnt < k) { k -= cnt; ans++; } else { k--; ans *= 10 ; } } return ans; } int getCnt (int x, int limit) { String a = String.valueOf(x), b = String.valueOf(limit); int n = a.length(), m = b.length(), k = m - n; int ans = 0 , u = Integer.parseInt(b.substring(0 , n)); for (int i = 0 ; i < k; i++) ans += Math.pow(10 , i); if (u > x) ans += Math.pow(10 , k); else if (u == x) ans += limit - x * Math.pow(10 , k) + 1 ; return ans; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 public int reverse (int x) { int res = 0 ; while (x!=0 ) { int tmp = x%10 ; if (res>214748364 || (res==214748364 && tmp>7 )) { return 0 ; } if (res<-214748364 || (res==-214748364 && tmp<-8 )) { return 0 ; } res = res*10 + tmp; x /= 10 ; } return res; } public int myAtoi (String s) { int res=0 , up=Integer.MAX_VALUE/10 ; int i=0 ,sign =1 ,len=s.length(); if (len==0 )return 0 ; while (s.charAt(i)==' ' ){ if (++i==len)return 0 ; } if (s.charAt(i)=='-' )sign=-1 ; if (s.charAt(i)=='-' ||s.charAt(i)=='+' )i++; for (int j=i;j<len;j++){ if (s.charAt(j) < '0' || s.charAt(j) > '9' ) break ; if (res > up || res == up && s.charAt(j) > '7' ) return sign == 1 ? Integer.MAX_VALUE : Integer.MIN_VALUE; res = res * 10 + (s.charAt(j) - '0' ); } return sign*res; }
阿拉伯数字和中文数字转换 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 public static string NumberToChinese (uint num) { string result = "" ; if (num == 0 ) { return "零" ; } uint _num = num; string[] chn_str = new string [] { "零" ,"一" , "二" , "三" , "四" , "五" , "六" , "七" , "八" , "九" }; string[] section_value = new string [] { "" ,"万" ,"亿" ,"万亿" }; string[] unit_value = new string [] { "" , "十" , "百" , "千" }; uint section = _num % 10000 ; for (int i = 0 ; _num != 0 && i < 4 ; i++) { if (section == 0 ) { if (result.Length > 0 && result.Substring(0 , 1 ) != "零" ) { result = "零" + result; } _num = _num / 10000 ; section = _num % 10000 ; continue ; } result = section_value[i]+result; uint unit = section % 10 ; for (int j = 0 ; j<4 ; j++) { if (unit == 0 ) { if (result.Length > 0 && result.Substring(0 , 1 ) != "零" && result.Substring(0 , 1 ) != section_value[i]) { result = "零" + result; } } else { result = chn_str[unit] + unit_value[j] + result; } section = section / 10 ; unit = section % 10 ; } _num = _num / 10000 ; section = _num % 10000 ; } if (result.Length > 0 && result.Substring(0 , 1 ) == "零" ) { result = result.Substring(1 ); } return result; }
https://leetcode.cn/problems/perfect-rectangle/ )
图论 DFS 200、岛屿数量 本质是图的连通性的问题 寻找有多少个连通图
首先,网格结构中的格子有多少相邻结点?答案是上下左右四个。对于格子 (r, c) 来说(r 和 c 分别代表行坐标和列坐标),四个相邻的格子分别是 (r-1, c)、(r+1, c)、(r, c-1)、(r, c+1)。换句话说,网格结构是「四叉」的。
其次,网格 DFS 中的 base case 是什么?从二叉树的 base case 对应过来,应该是网格中不需要继续遍历、grid[r][c] 会出现数组下标越界异常的格子,也就是那些超出网格范围的格子。
这一点稍微有些反直觉,坐标竟然可以临时超出网格的范围?这种方法我称为「先污染后治理」—— 甭管当前是在哪个格子,先往四个方向走一步再说,如果发现走出了网格范围再赶紧返回。这跟二叉树的遍历方法是一样的,先递归调用,发现 root == null 再返回。
这样,我们得到了网格 DFS 遍历的框架代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 void dfs (int [][] grid, int r, int c) { if (!inArea(grid, r, c)) { return ; } dfs(grid, r - 1 , c); dfs(grid, r + 1 , c); dfs(grid, r, c - 1 ); dfs(grid, r, c + 1 ); } boolean inArea (int [][] grid, int r, int c) { return 0 <= r && r < grid.length && 0 <= c && c < grid[0 ].length; }
破题点在于沿边遍历这样可以分开寻找到能流进Atlantic 和Pacific的岛屿然后求交集就可以知道位置
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 for (int i = 0 ; i < m; i++) { dfs3(pacific,i, 0 , heights); } for (int j = 1 ; j < n; j++) { dfs3(pacific,0 , j, heights); } for (int i = 0 ; i < m; i++) { dfs3(atlantic,i, n - 1 ,heights ); } for (int j = 0 ; j < n - 1 ; j++) { dfs3(atlantic,m - 1 , j, heights); } public void dfs3 (boolean [][]ocean,int i,int j,int [][]height) { if (ocean[i][j])return ; ocean[i][j]=true ; for (int [] dir : dirs) { int newi=i+dir[0 ],newj=j+dir[1 ]; if (newi>=0 && newi<height.length && newj>=0 && newj<height[0 ].length && height[newi][newj]>=height[i][j]) dfs3(ocean,newi,newj,height); } }
此题同上一题类似寻找四周岛屿影响的内部岛屿
此题融合了二分查找与dfs并存,使用二分查找来寻找到从左到右的最小路径。这是本问题具有的单调性。因此可以使用二分查找定位到最短等待时间。具体来说:在区间 [0, N * N - 1] 里猜一个整数,针对这个整数从起点(左上角)开始做一次深度优先遍历或者广度优先遍历。
当小于等于该数值时,如果存在一条从左上角到右下角的路径,说明答案可能是这个数值,也可能更小;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 private int N; public static final int [][] DIRECTIONS = {{0 , 1 }, {0 , -1 }, {1 , 0 }, {-1 , 0 }}; public int swimInWater (int [][] grid) { this .N=grid.length; int left = 0 ; int right = N * N - 1 ; while (left < right) { int mid=(left+right)/2 ; boolean used [][]=new boolean [N][N]; if (grid[0 ][0 ]<=mid&&dfs(grid,0 ,0 ,used,mid)){ right=mid; } else left=mid+1 ; } return right; } private boolean dfs (int [][] grid, int x, int y, boolean [][] used, int mid) { used[x][y] = true ; for (int dic[]:DIRECTIONS){ int newx=x+dic[0 ]; int newy=y+dic[1 ]; if (inArea(newx,newy)&&!used[newx][newy]&&grid[newx][newy]<=mid){ if (newx == N - 1 && newy == N - 1 ) { return true ; } if (dfs(grid, newx, newy, used, mid)) { return true ; } } } return false ; } private boolean inArea (int x, int y) { return x >= 0 && x < N && y >= 0 && y < N; }
按照树的遍历来计算所存在的边数方法一:Hierholzer 算法
Hierholzer 算法用于在连通图中寻找欧拉路径,其流程如下:
从起点出发,进行深度优先搜索。
每次沿着某条边从某个顶点移动到另外一个顶点的时候,都需要删除这条边。
如果没有可移动的路径,则将所在节点加入到栈中,并返回。
当我们顺序地考虑该问题时,我们也许很难解决该问题,因为我们无法判断当前节点的哪一个分支是「死胡同」分支。
不妨倒过来思考。我们注意到只有那个入度与出度差为 111 的节点会导致死胡同。而该节点必然是最后一个遍历到的节点。我们可以改变入栈的规则,当我们遍历完一个节点所连的所有节点后,我们才将该节点入栈(即逆序入栈)。
对于当前节点而言,从它的每一个非「死胡同」分支出发进行深度优先搜索,都将会搜回到当前节点。而从它的「死胡同」分支出发进行深度优先搜索将不会搜回到当前节点。也就是说当前节点的死胡同分支将会优先于其他非「死胡同」分支入栈。
这样就能保证我们可以「一笔画」地走完所有边,最终的栈中逆序地保存了「一笔画」的结果。我们只要将栈中的内容反转,即可得到答案。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 Map<String, PriorityQueue<String>> map=new HashMap <>(); List<String> res = new LinkedList <>(); public List<String> findItinerary (List<List<String>> tickets) { for (List<String> list:tickets){ String src = list.get(0 );String des=list.get(1 ); if (!map.containsKey(src)){ map.put(src,new PriorityQueue <>()); } map.get(src).add(des); } dfs("JHK" ); Collections.reverse(res); return res; } public void dfs (String src) { while (map.containsKey(src) && map.get(src).size() > 0 ) { dfs(map.get(src).poll()); } res.add(src); }
按照题目要求构建出树,然后dfs遍历遇到阻塞就跳过
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 int res=1 ; public int reachableNodes (int n, int [][] edges, int [] restricted) { ArrayList <Integer>[]list=new ArrayList [n]; for (int i = 0 ; i < n; i++) { list[i] = new ArrayList <Integer>(); } for (int []edge:edges){ list[edge[0 ]].add(edge[1 ]); list[edge[1 ]].add(edge[0 ]); } boolean [] vis = new boolean [n]; for (int r : restricted) vis[r] = true ; dfs(list,vis,0 ); return res; } public void dfs (List<Integer>[] g, boolean [] vis, int fa) { vis[fa]=true ; for (int child:g[fa]){ if (vis[child])continue ; res++; dfs(g,vis,child); } }
换根dp 思路都为优先算出一次dfs从0开始的树初始情况,然后因为换节点只会影响该节点与其子节点关系所以使用dp公式保存遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 private List<Integer>[] times; private Set<Long> s = new HashSet <>(); private int k, res, cnt0; public int rootCount (int [][] edges, int [][] guesses, int k) { this .k = k; times = new ArrayList [edges.length + 1 ]; Arrays.setAll(times, i -> new ArrayList <>()); for (int [] e : edges) { int x = e[0 ]; int y = e[1 ]; times[x].add(y); times[y].add(x); } for (int [] e : guesses) { s.add((long ) e[0 ] << 32 | e[1 ]); } dfs(0 , -1 ); reroot(0 , -1 , cnt0); return res; } private void dfs (int x, int fa) { for (int y : times[x]) { if (y != fa) { if (s.contains((long ) x << 32 | y)) { cnt0++; } dfs(y, x); } } } private void reroot (int x, int fa, int cnt) { if (cnt >= k) { res++; } for (int y : times[x]) { if (y != fa) { int c = cnt; if (s.contains((long ) x << 32 | y)) c--; if (s.contains((long ) y << 32 | x)) c++; reroot(y, x, c); } } } private List<Integer>[] g; private int [] ans, size; public int [] sumOfDistancesInTree(int n, int [][] edges) { g = new ArrayList [n]; Arrays.setAll(g, e -> new ArrayList <>()); for (int [] e : edges) { int x = e[0 ], y = e[1 ]; g[x].add(y); g[y].add(x); } ans = new int [n]; size = new int [n]; dfs(0 , -1 , 0 ); reroot(0 , -1 ); return ans; } private void dfs (int x, int fa, int depth) { ans[0 ] += depth; size[x] = 1 ; for (int y : g[x]) { if (y != fa) { dfs(y, x, depth + 1 ); size[x] += size[y]; } } } private void reroot (int x, int fa) { for (int y : g[x]) { if (y != fa) { ans[y] = ans[x] + g.length - 2 * size[y]; reroot(y, x); } } }
BFS BFS 可以看成是层序遍历。从某个结点出发,BFS 首先遍历到距离为 1 的结点,然后是距离为 2、3、4…… 的结点。因此,BFS 可以用来求最短路径问题。BFS 先搜索到的结点,一定是距离最近的结点。
再看看这道题的题目要求:返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。翻译一下,实际上就是求腐烂橘子到所有新鲜橘子的最短路径。那么这道题使用 BFS,应该是毫无疑问的了。
如何写(最短路径的) BFS 代码
1 2 3 4 5 while queue 非空: node = queue.pop() for node 的所有相邻结点 m: if m 未访问过: queue.push(m)
但是用 BFS 来求最短路径的话,这个队列中第 1 层和第 2 层的结点会紧挨在一起,无法区分。因此,我们需要稍微修改一下代码,在每一层遍历开始前,记录队列中的结点数量 nnn ,然后一口气处理完这一层的 nnn 个结点。代码框架是这样的:
1 2 3 4 5 6 7 8 9 depth = 0 while queue 非空: depth++ n = queue 中的元素个数 循环 n 次: node = queue.pop() for node 的所有相邻结点 m: if m 未访问过: queue.push(m)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 public int orangesRotting (int [][] grid) { int l=grid.length; int c=grid[0 ].length; Queue<int []> queue=new LinkedList <>(); int count=0 ; for (int i = 0 ; i < l; i++) { for (int j = 0 ; j < c; j++) { if (grid[i][j]==1 ){ count++; } else if (grid[i][j]==2 ) { queue.add(new int []{i,j}); } } } int res=0 ; while (!queue.isEmpty()&&count>0 ){ res++; int n = queue.size(); for (int i = 0 ; i < n; i++) { int []bad=queue.poll(); int j=bad[0 ]; int k=bad[1 ]; if (j-1 >= 0 && grid[j-1 ][k] == 1 ) { grid[j-1 ][k]=2 ; count--; queue.add(new int []{j-1 ,k}); } if (j+1 <l && grid[j+1 ][k] == 1 ) { grid[j+1 ][k]=2 ; count--; queue.add(new int []{j+1 ,k}); } if (k-1 >= 0 && grid[j][k-1 ] == 1 ) { grid[j][k-1 ]=2 ; count--; queue.add(new int []{j,k-1 }); } if (k+1 <c && grid[j][k+1 ] == 1 ) { grid[j][k+1 ]=2 ; count--; queue.add(new int []{j,k+1 }); } } } if (count>0 )return -1 ; else return res; }
bfs 按照每一列满足条件的加入 遍历了无元素加入为止
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public int maxMoves (int [][] grid) { int m = grid.length, n = grid[0 ].length; Set<Integer> q = new HashSet <>(); for (int i = 0 ; i < m; i++) { q.add(i); } for (int j = 1 ; j < n; j++) { Set<Integer> q2 = new HashSet <>(); for (int i : q) { for (int i2 = i - 1 ; i2 <= i + 1 ; i2++) { if (0 <= i2 && i2 < m && grid[i][j - 1 ] < grid[i2][j]) { q2.add(i2); } } } q = q2; if (q.isEmpty()) { return j - 1 ; } } return n - 1 ; }
拓扑结构(拓扑排序) 这是一个包含 n个节点的有向图 G我们需要判断此有向图是否存在环路
我们将每一门课看成一个节点;
如果想要学习课程 A之前必须完成课程 B,那么我们从 B 到 A连接一条有向边。这样以来,在拓扑排序中,B 一定出现在 A 的前面。
DFS思路
直接遍历,如果入度为0那么进行对其下一门课程遍历,如果一直到最后末尾都不会回到之前的课程那么则无环
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 List<List<Integer>> edges; int [] visited; boolean valid = true ; public boolean canFinish (int numCourses, int [][] prerequisites) { edges = new ArrayList <List<Integer>>(); for (int i = 0 ; i < numCourses; ++i) { edges.add(new ArrayList <Integer>()); } visited = new int [numCourses]; for (int [] info : prerequisites) { edges.get(info[1 ]).add(info[0 ]); } for (int i = 0 ; i < numCourses && valid; ++i) { if (visited[i] == 0 ) { dfs(i); } } return valid; } public void dfs (int u) { visited[u] = 1 ; for (int v: edges.get(u)) { if (visited[v] == 0 ) { dfs(v); if (!valid) { return ; } } else if (visited[v] == 1 ) { valid = false ; return ; } } visited[u] = 2 ; }
BFS思路
我们先统计出入度为0 的项目的个数,遍历入度为0的节点,然后减少入度如果减少到也变成入度为0时加入,如果所有节点被加入那么就不存在环
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution { List<List<Integer>> edges; int [] indeg; public boolean canFinish (int numCourses, int [][] prerequisites) { edges = new ArrayList <List<Integer>>(); for (int i = 0 ; i < numCourses; ++i) { edges.add(new ArrayList <Integer>()); } indeg = new int [numCourses]; for (int [] info : prerequisites) { edges.get(info[1 ]).add(info[0 ]); ++indeg[info[0 ]]; } Queue<Integer> queue = new LinkedList <Integer>(); for (int i = 0 ; i < numCourses; ++i) { if (indeg[i] == 0 ) { queue.offer(i); } } int visited = 0 ; while (!queue.isEmpty()) { ++visited; int u = queue.poll(); for (int v: edges.get(u)) { --indeg[v]; if (indeg[v] == 0 ) { queue.offer(v); } } } return visited == numCourses; } }
BFS
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 class Solution { List<List<Integer>> edges; int [] indeg; int [] result; int index; public int [] findOrder(int numCourses, int [][] prerequisites) { edges = new ArrayList <List<Integer>>(); for (int i = 0 ; i < numCourses; ++i) { edges.add(new ArrayList <Integer>()); } indeg = new int [numCourses]; result = new int [numCourses]; index = 0 ; for (int [] info : prerequisites) { edges.get(info[1 ]).add(info[0 ]); ++indeg[info[0 ]]; } Queue<Integer> queue = new LinkedList <Integer>(); for (int i = 0 ; i < numCourses; ++i) { if (indeg[i] == 0 ) { queue.offer(i); } } while (!queue.isEmpty()) { int u = queue.poll(); result[index++] = u; for (int v: edges.get(u)) { --indeg[v]; if (indeg[v] == 0 ) { queue.offer(v); } } } if (index != numCourses) { return new int [0 ]; } return result; } }
蛇形棋因为行列关系在奇偶数行时不同使用一个n*n的数组在不同奇偶数情况时去处理行列 之后遍历每次6个点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public int snakesAndLadders (int [][] board) { int n = board.length; boolean [] vis = new boolean [n * n + 1 ]; Queue<int []> queue = new LinkedList <int []>(); queue.offer(new int []{1 ,0 }); while (!queue.isEmpty()){ int p[]=queue.poll(); for (int i = 1 ; i <=6 ; i++) { int next=p[0 ]+i; if (next>n*n)break ; int []post=id2rc(next,n); if (board[post[0 ]][post[1 ]]>0 )next=board[post[0 ]][post[1 ]]; if (next==n*n)return p[1 ]+1 ; if (!vis[next]){ vis[next]=true ; queue.offer(new int []{next,p[1 ]+1 }); } } } return -1 ; } public int [] id2rc(int id, int n) { int r = (id - 1 ) / n, c = (id - 1 ) % n; if (r % 2 == 1 ) { c = n - 1 - c; } return new int []{n - 1 - r, c}; }
每层搜索将字母依次替换,然后用Hashmap记录
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 static char [] items = new char []{'A' , 'C' , 'G' , 'T' }; public int minMutation (String startGene, String endGene, String[] bank) { Set<String> set = new HashSet <>(); for (String s : bank) set.add(s); Deque<String> d = new ArrayDeque <>(); Map<String, Integer> map = new HashMap <>(); d.addLast(startGene); map.put(startGene, 0 ); while (!d.isEmpty()){ int size=d.size(); while (size-->0 ){ String s=d.pollFirst(); char [] cs = s.toCharArray(); int step = map.get(s); for (int i=0 ;i<8 ;i++){ for (char c : items) { if (cs[i] == c) continue ; char [] clone = cs.clone(); clone[i] = c; String sub = String.valueOf(clone); if (!set.contains(sub)) continue ; if (map.containsKey(sub)) continue ; if (sub.equals(endGene)) return step + 1 ; map.put(sub, step + 1 ); d.addLast(sub); } } } } return -1 ; }
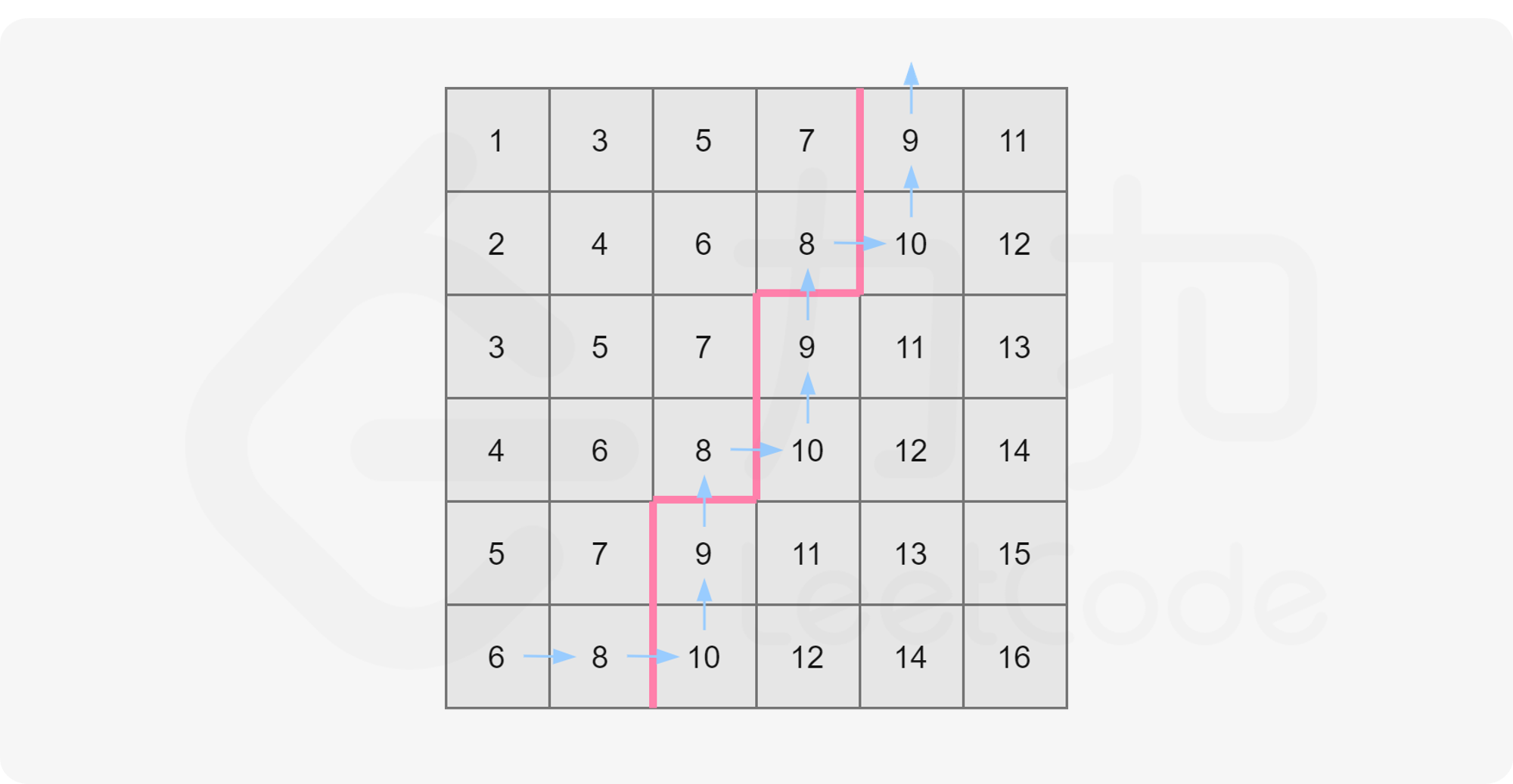




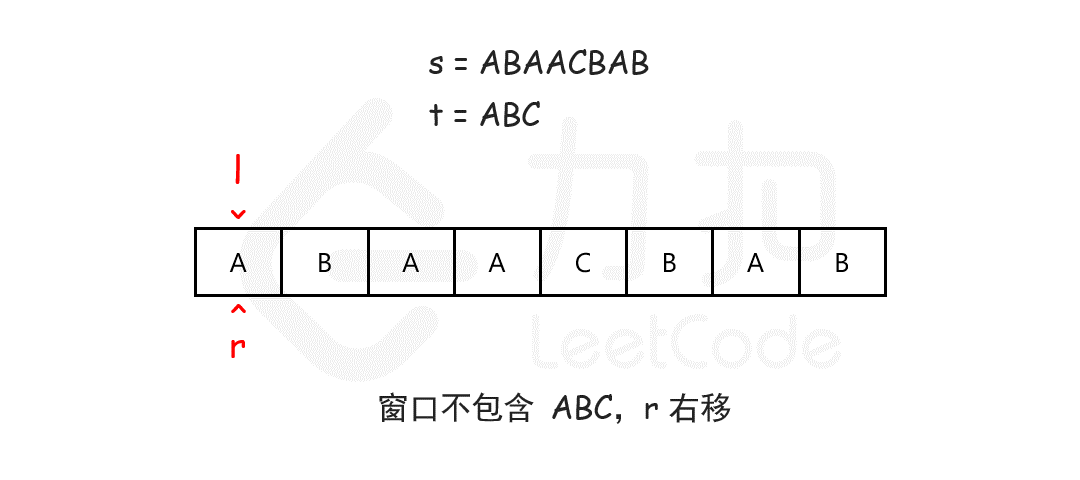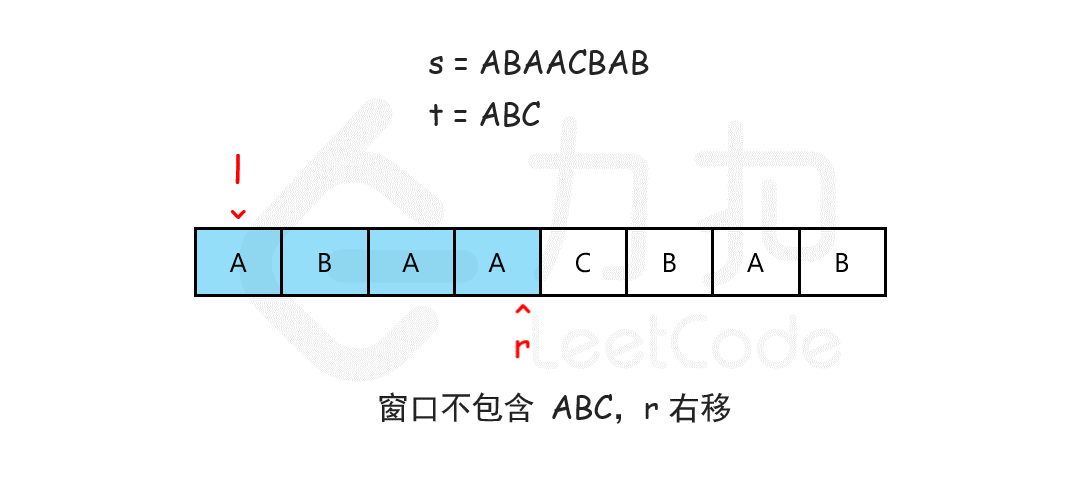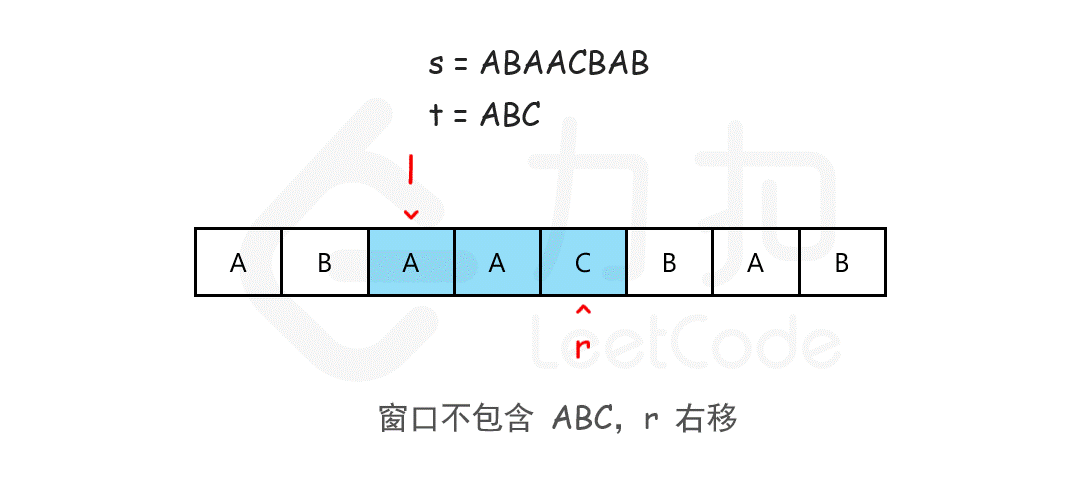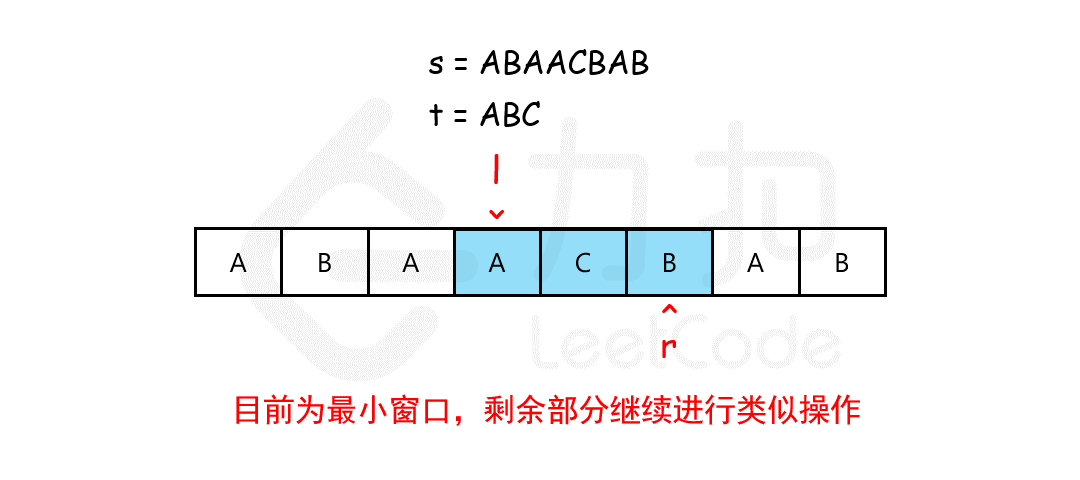
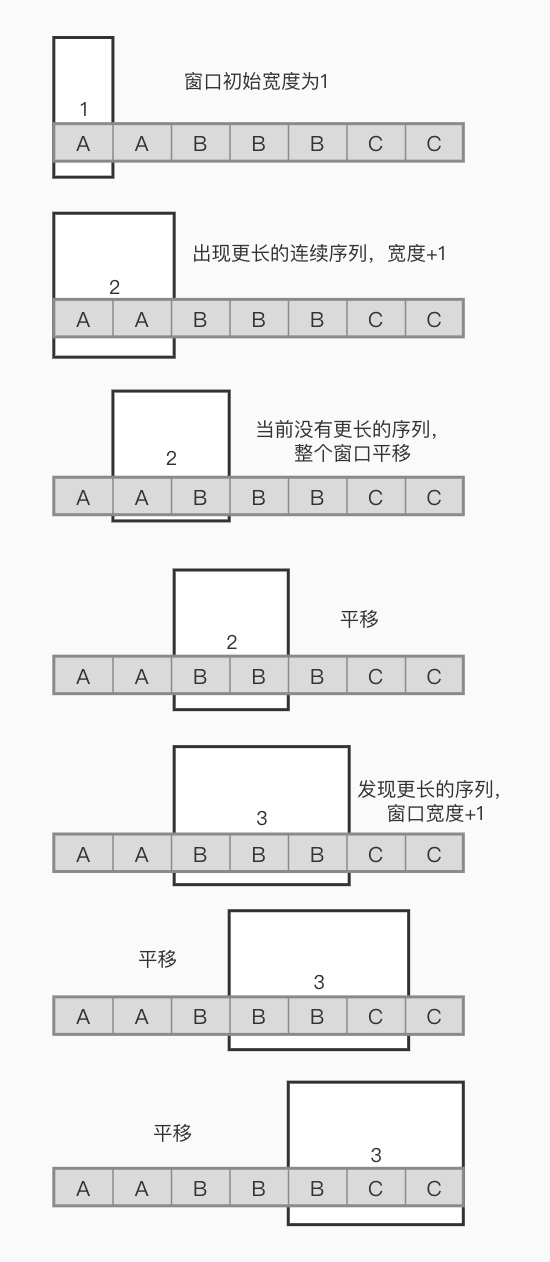
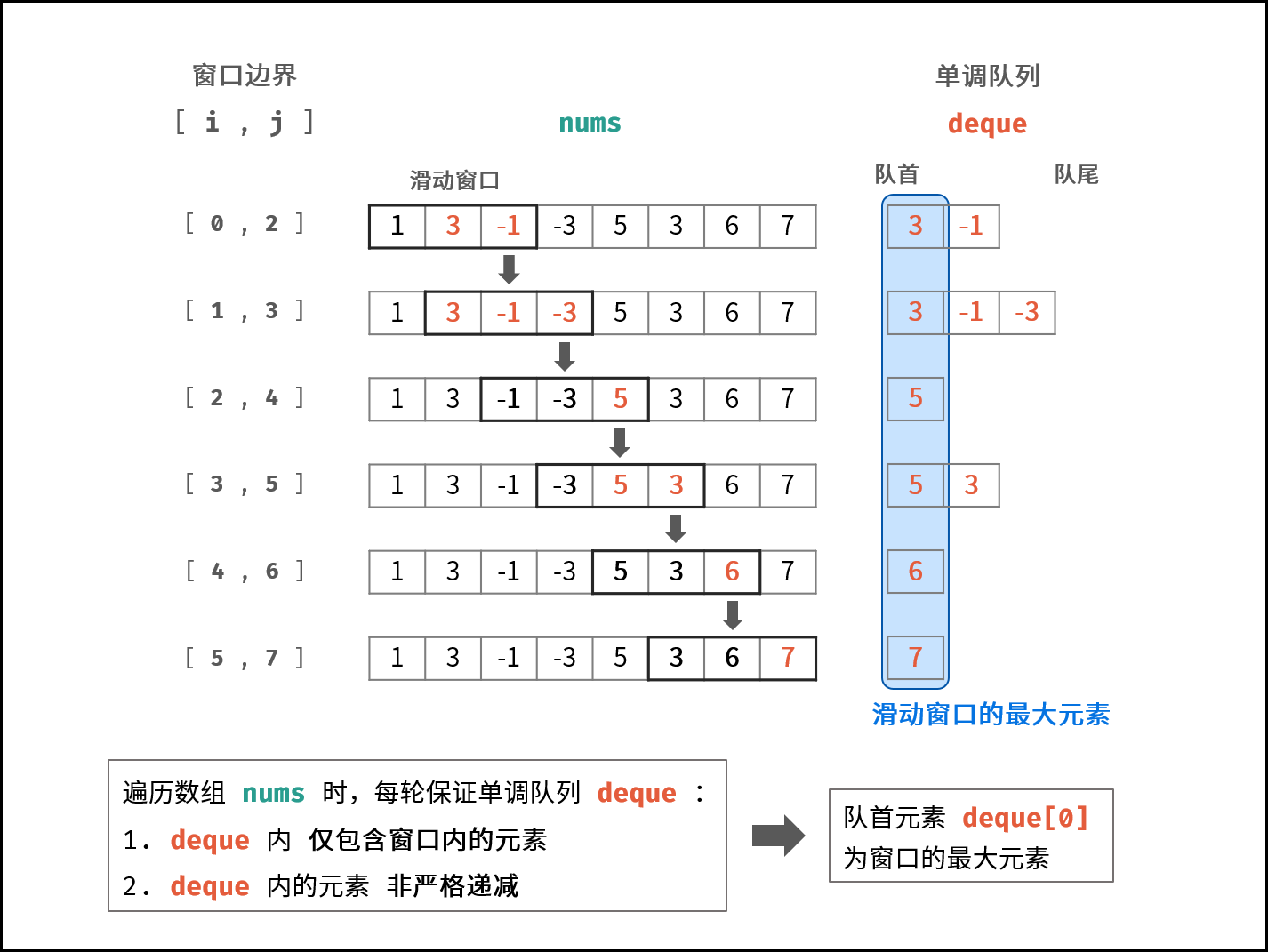
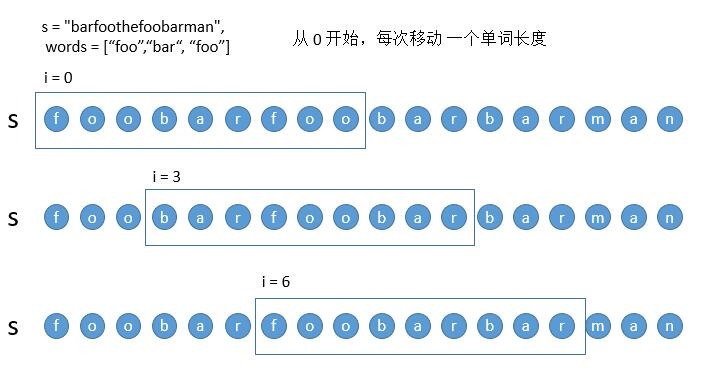

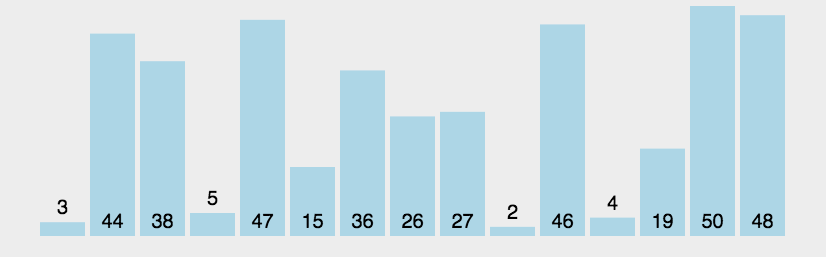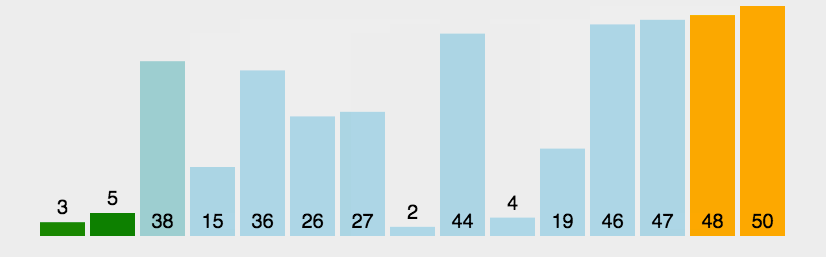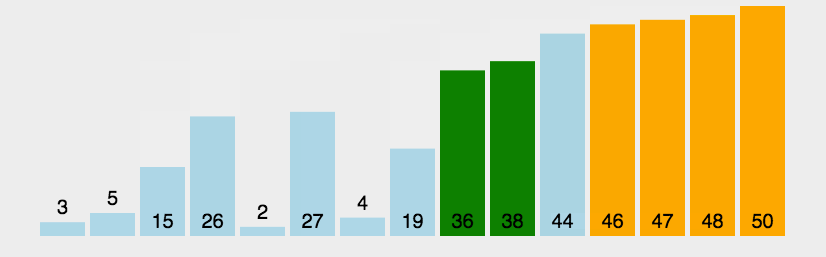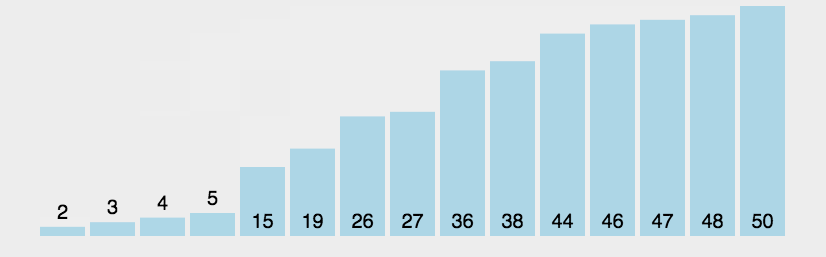
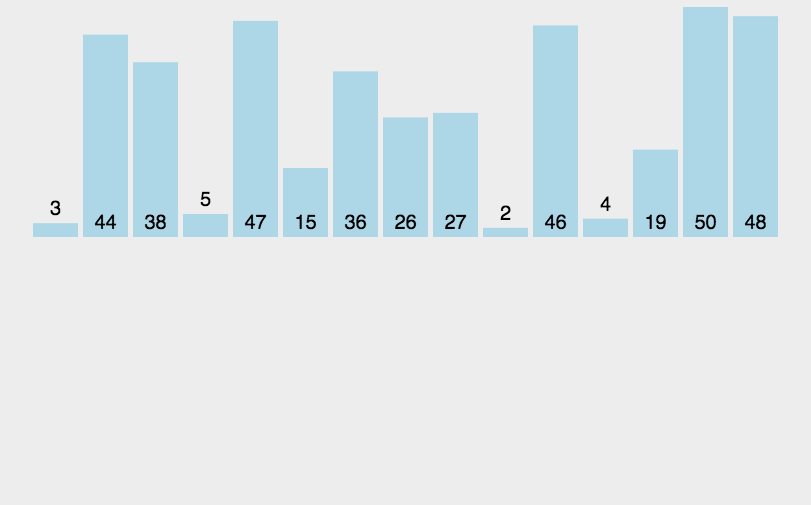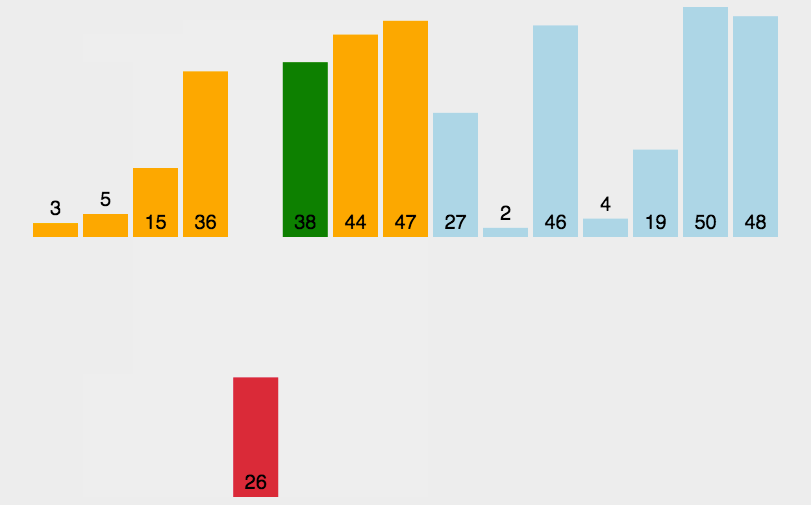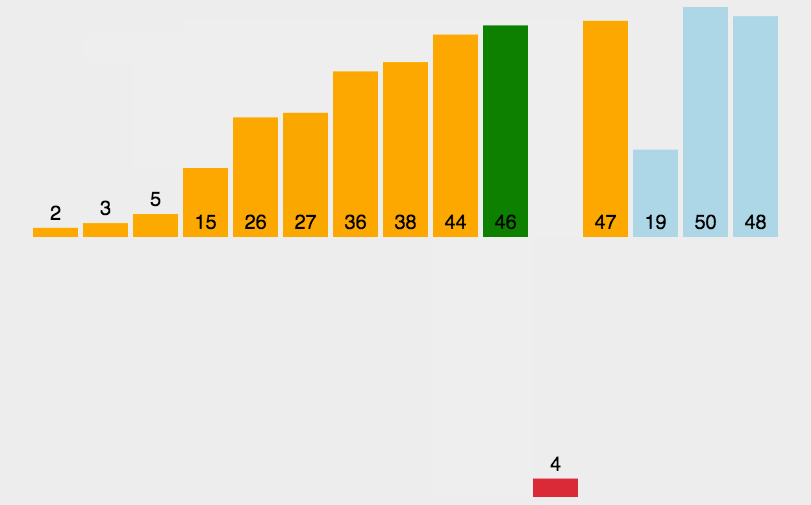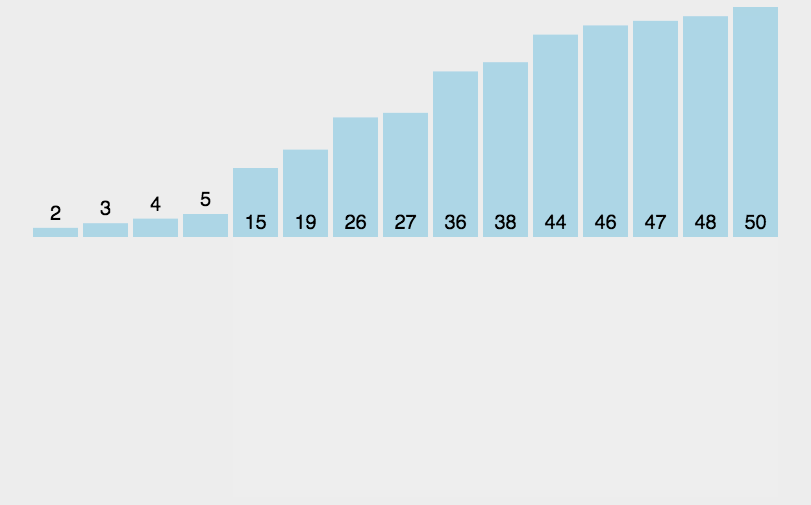
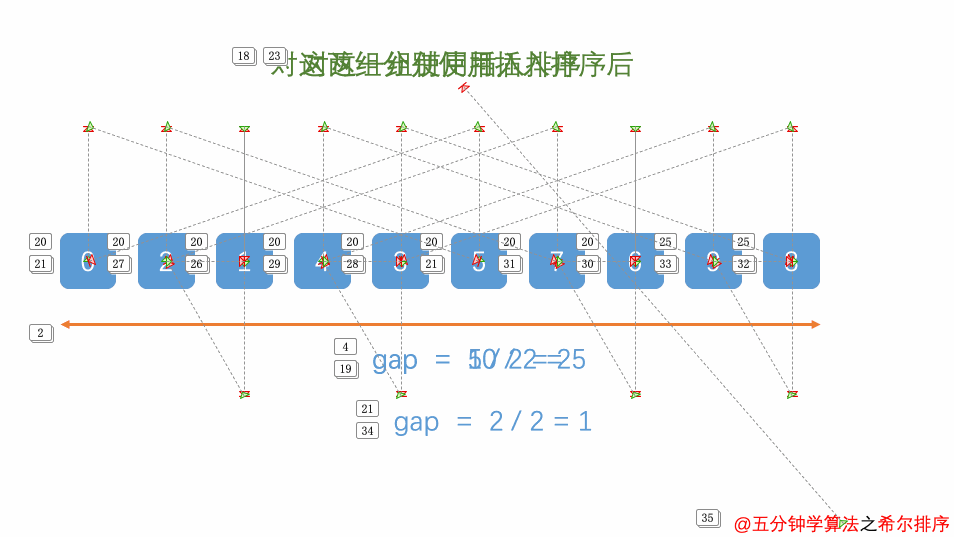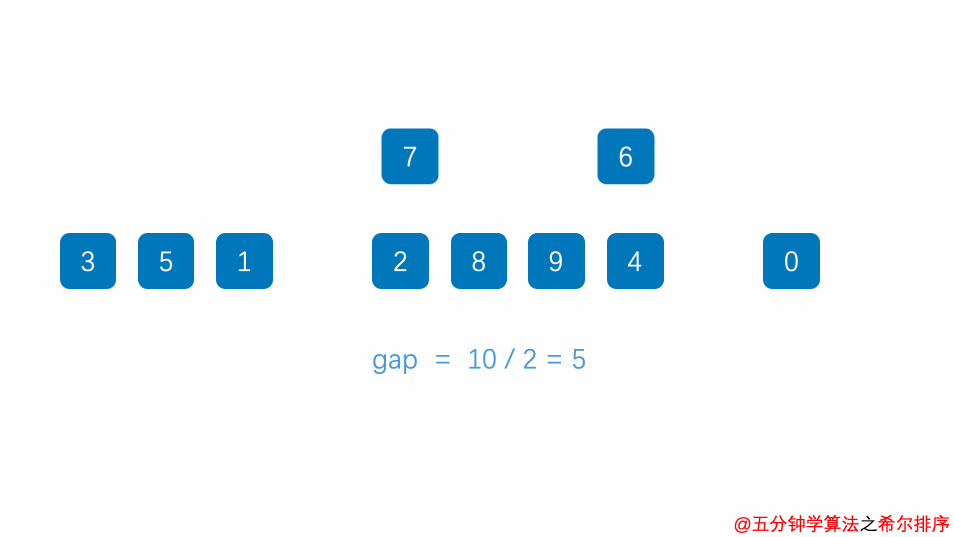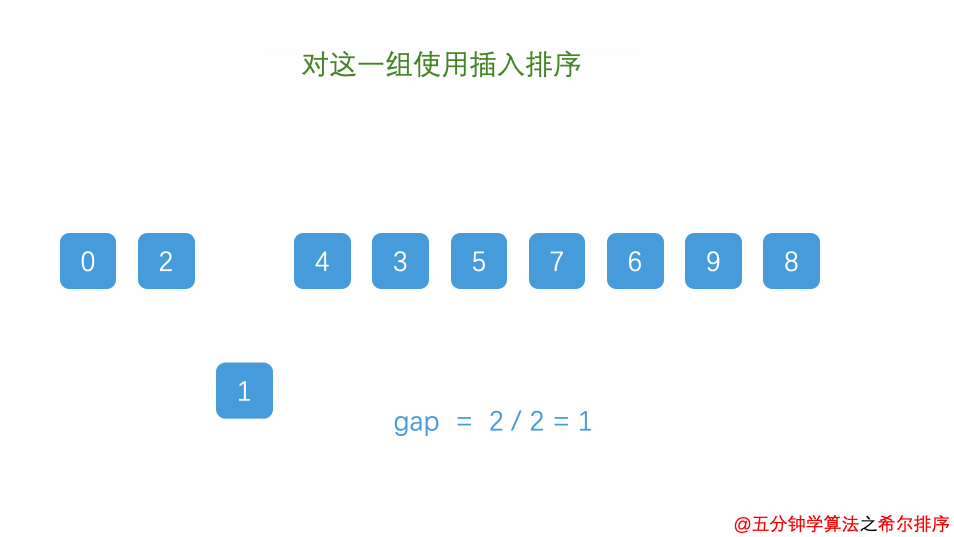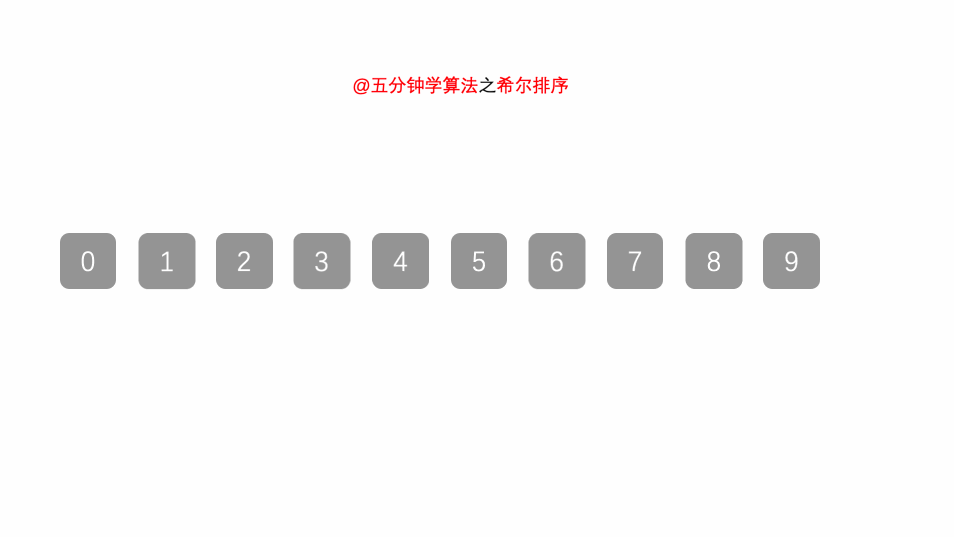

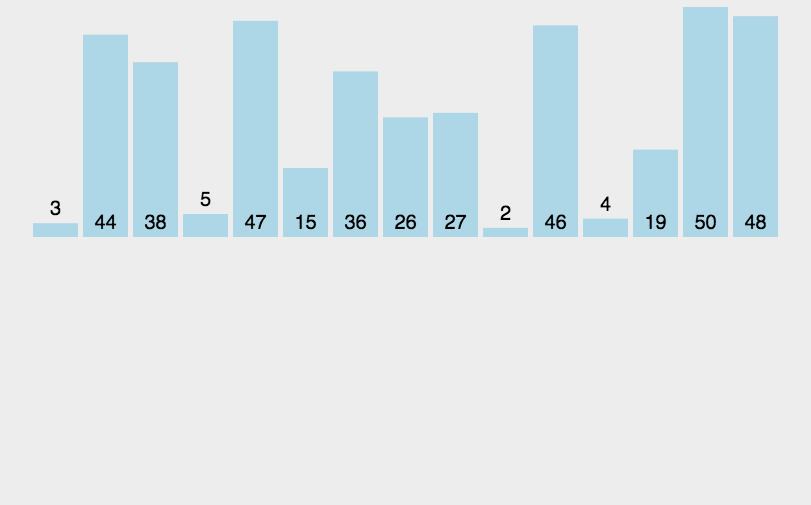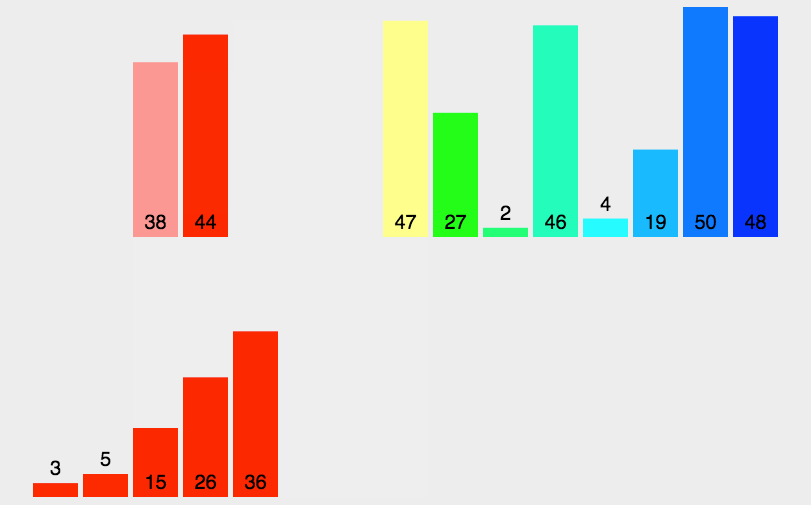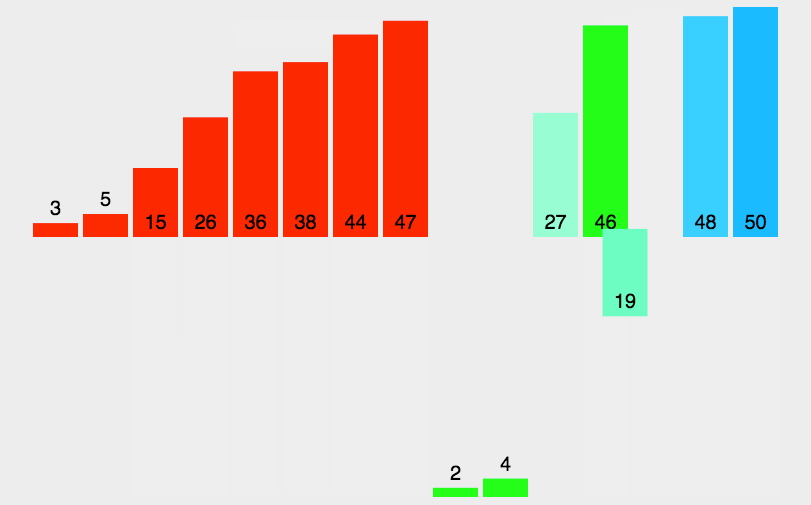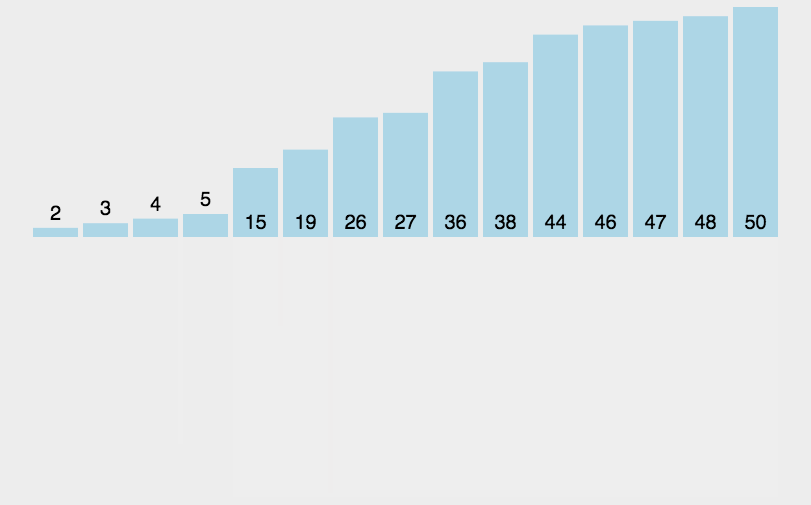

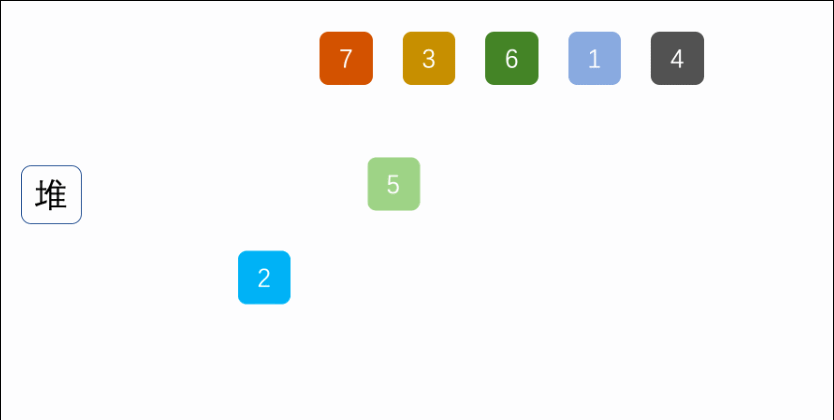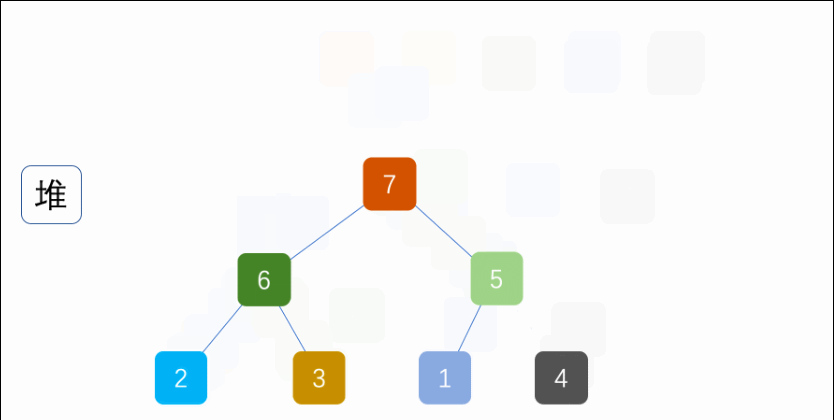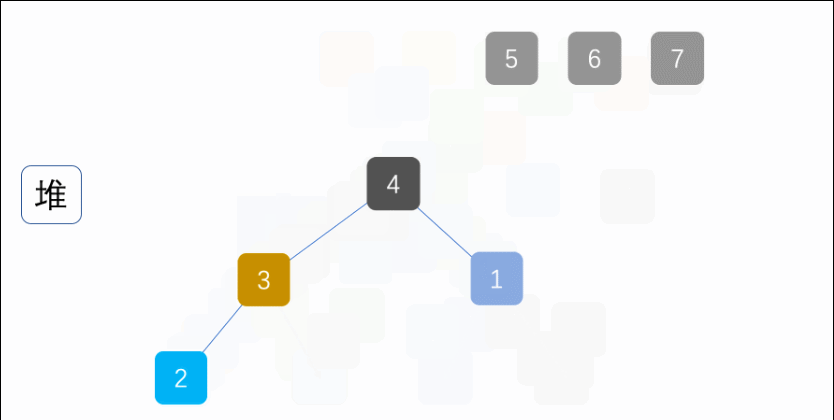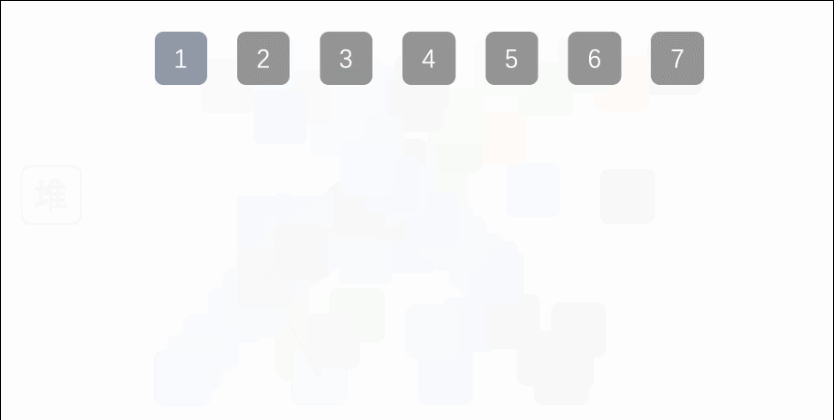




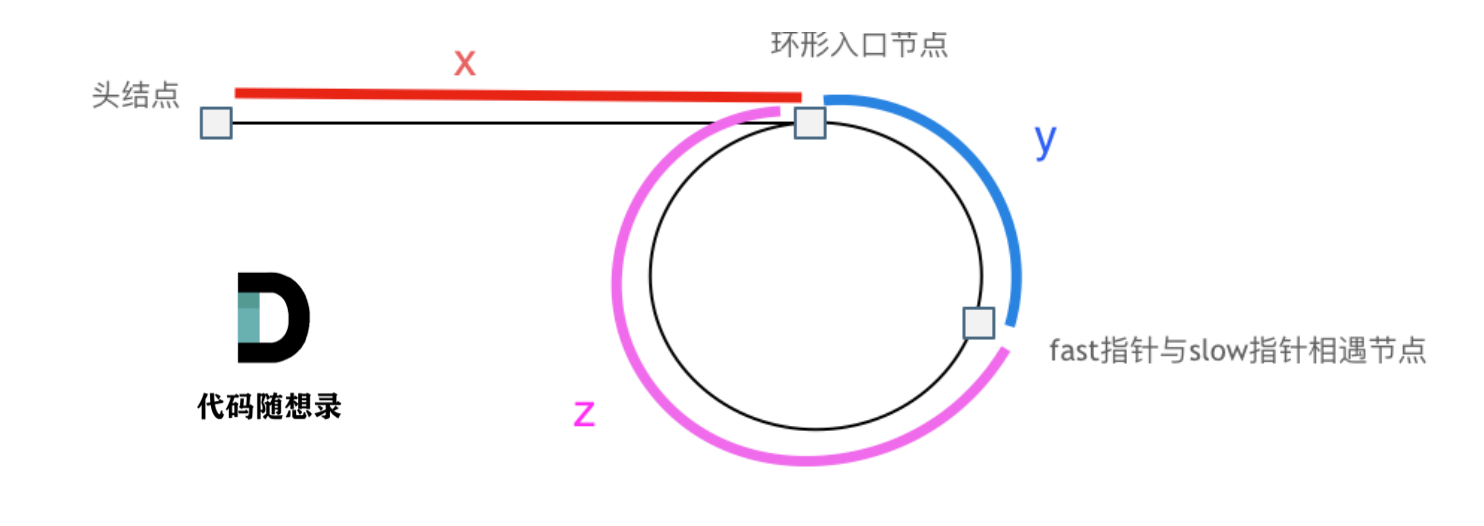



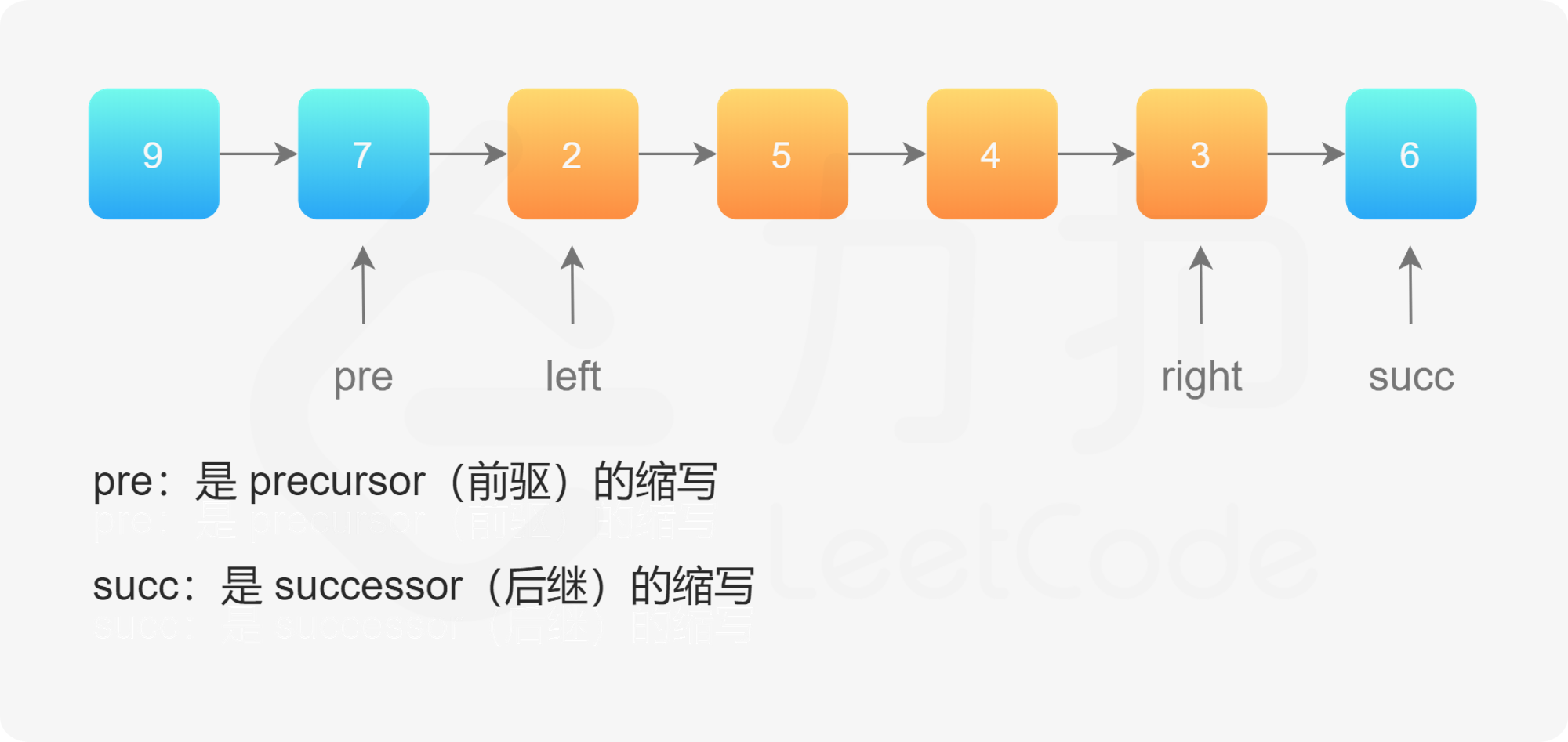
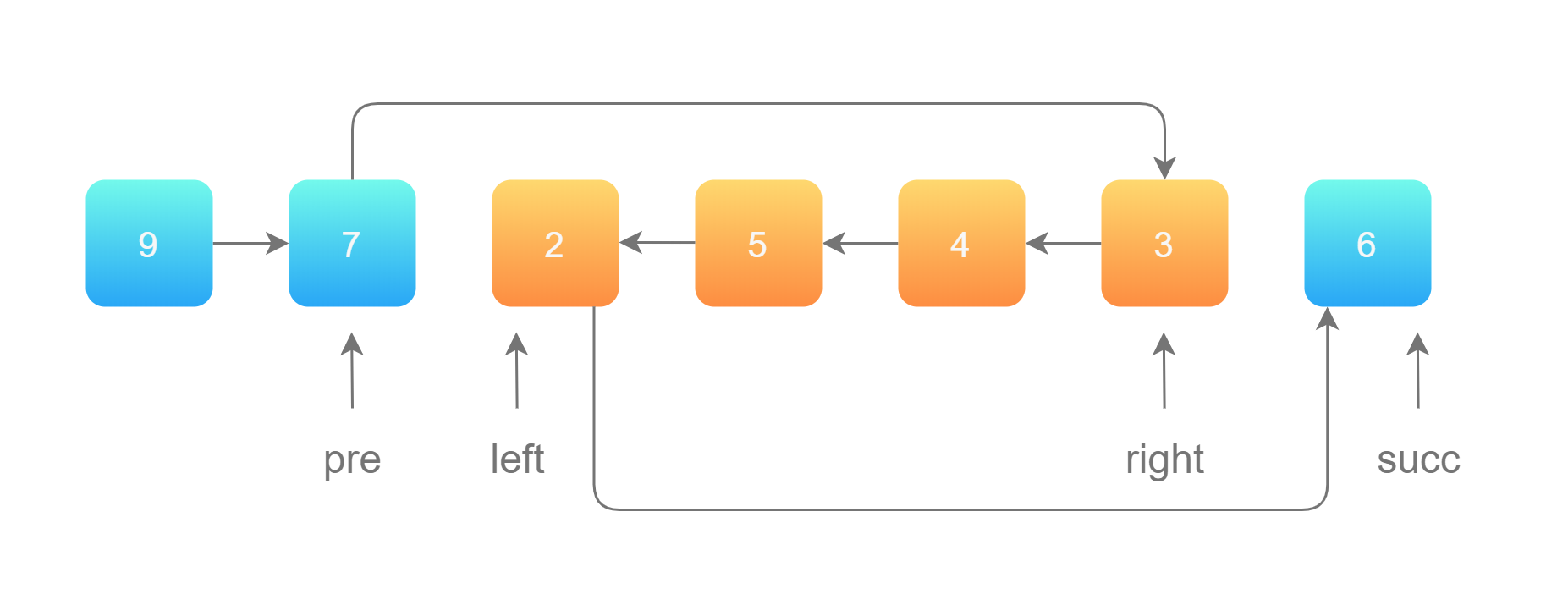

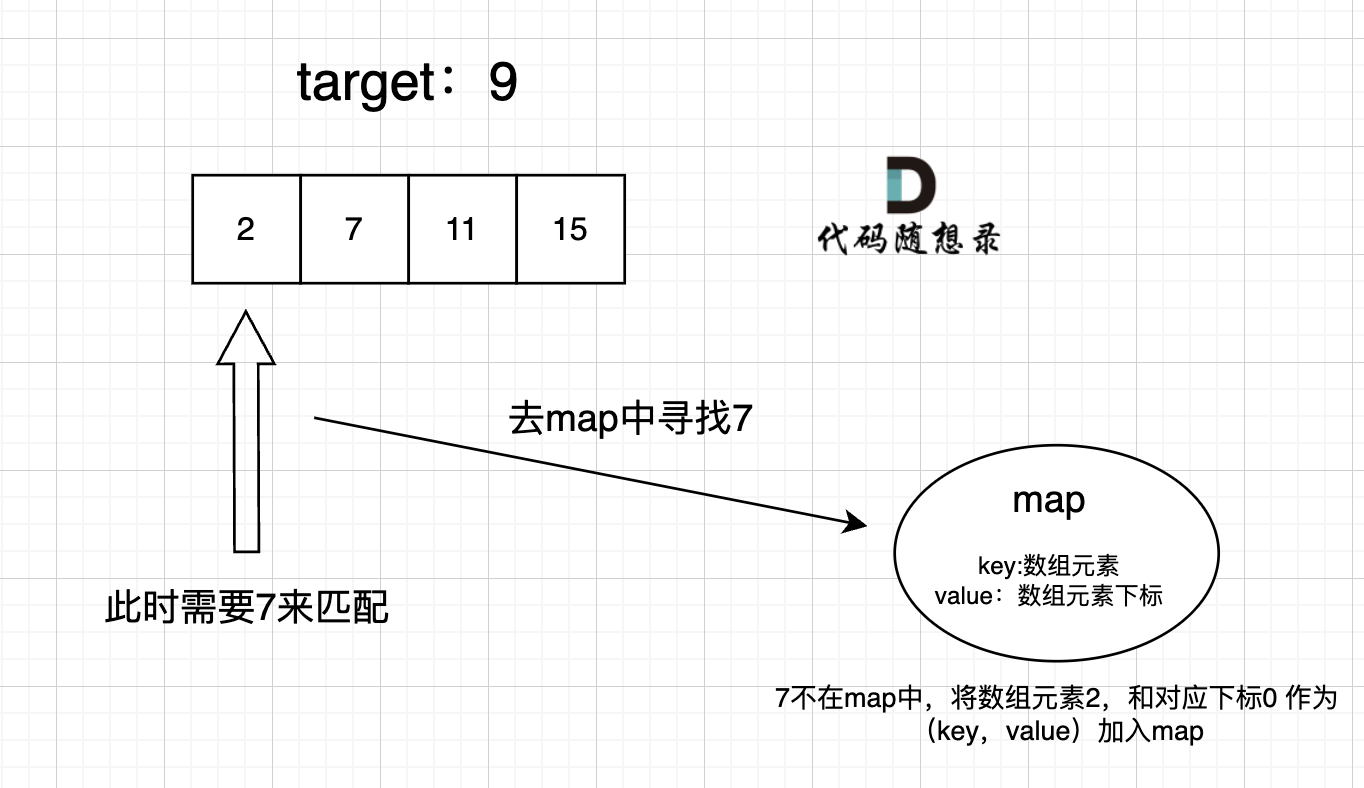
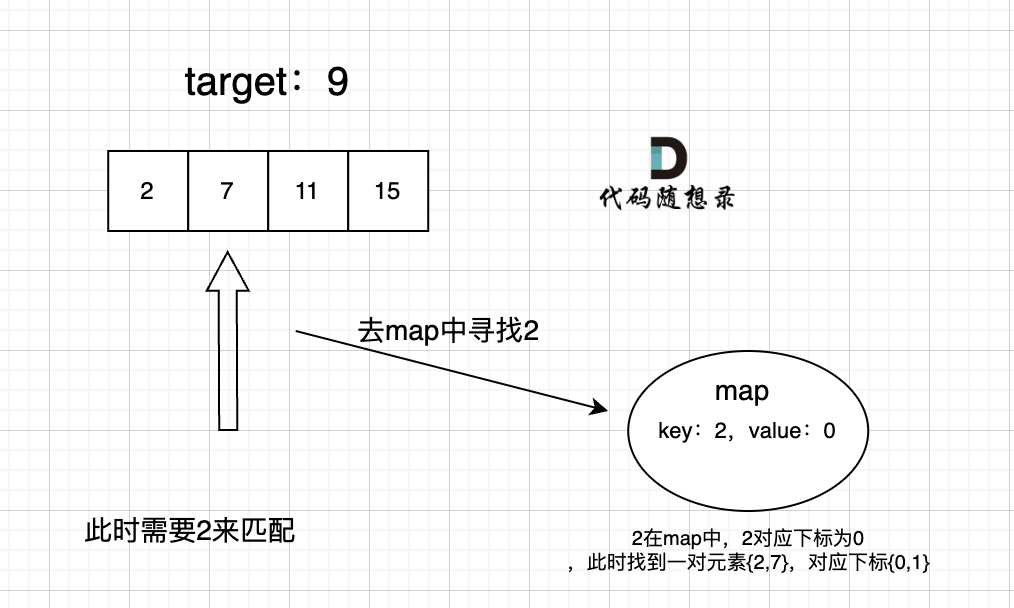


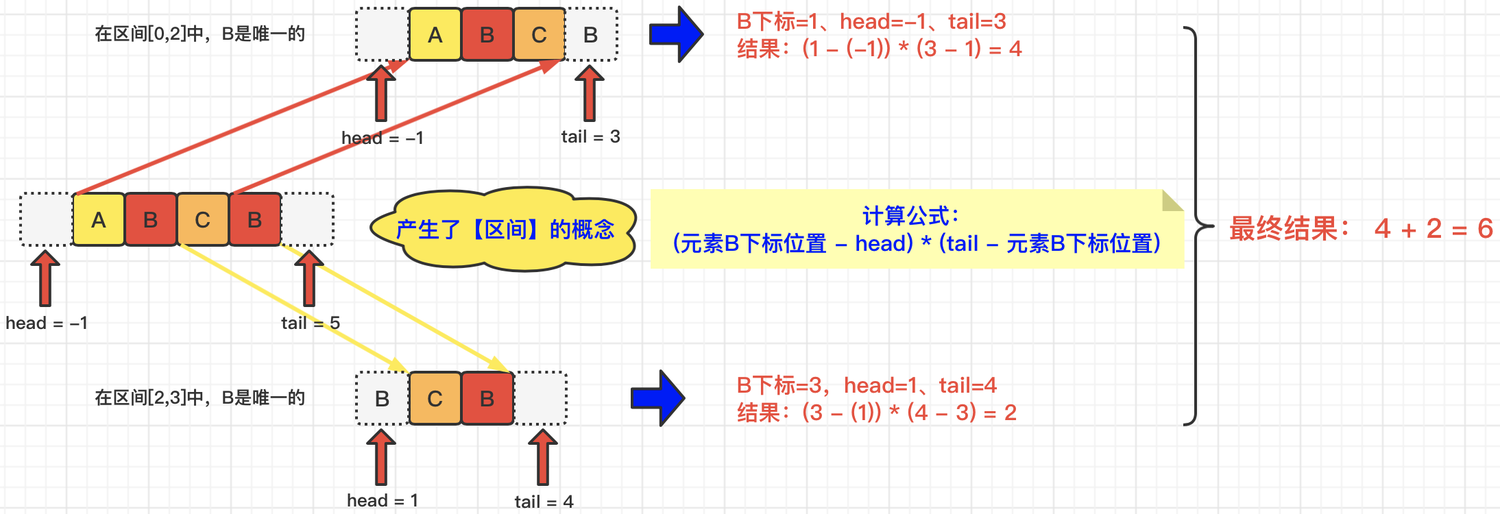
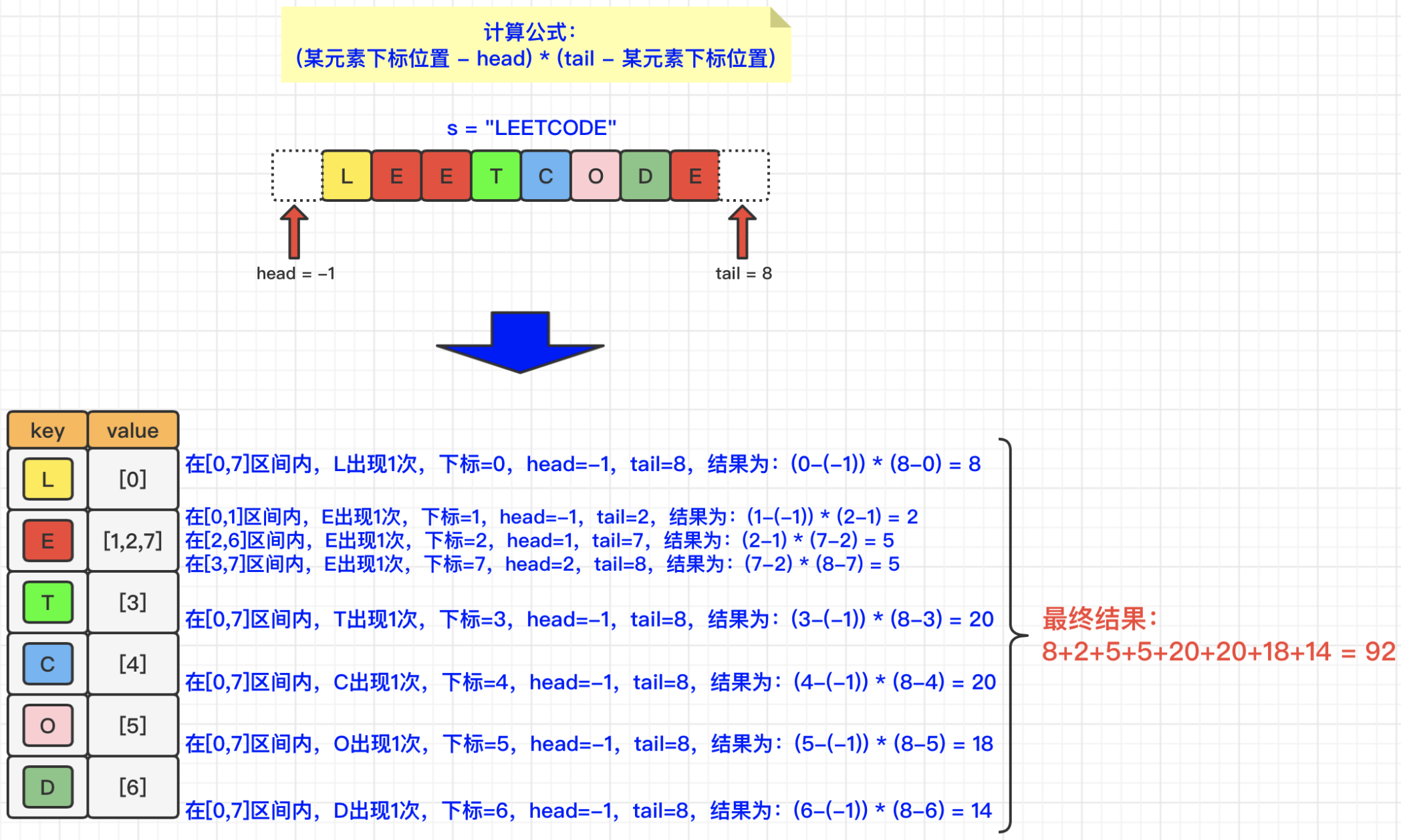











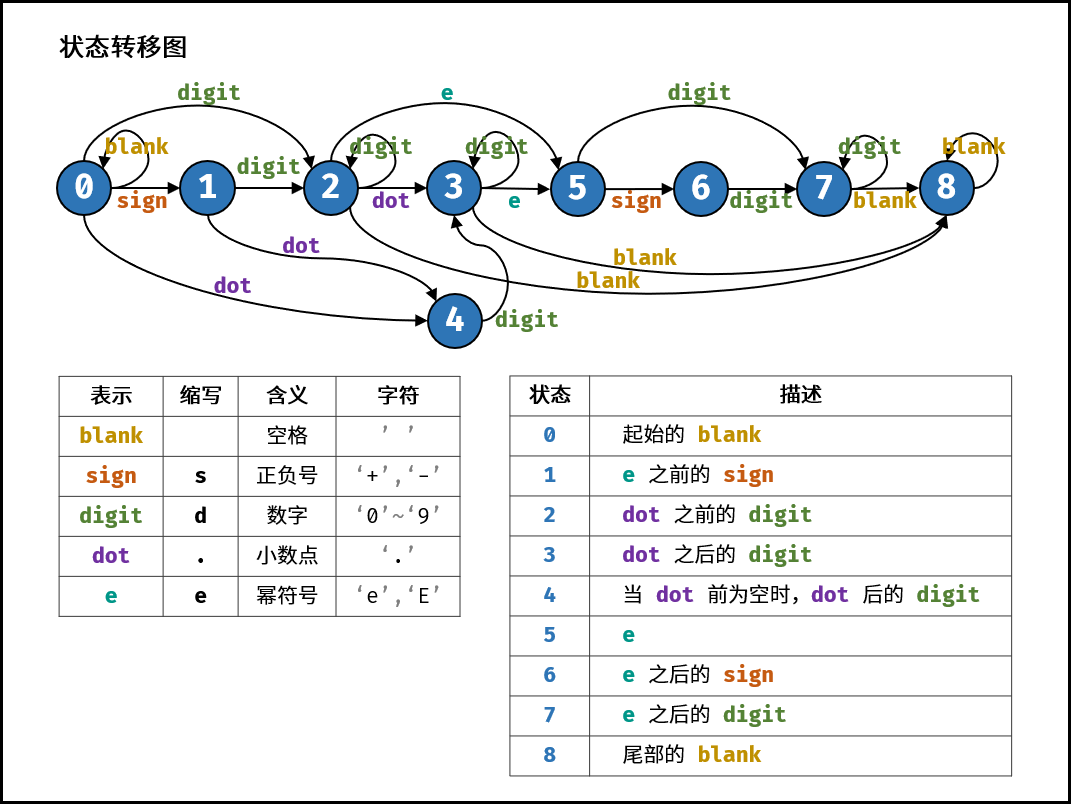
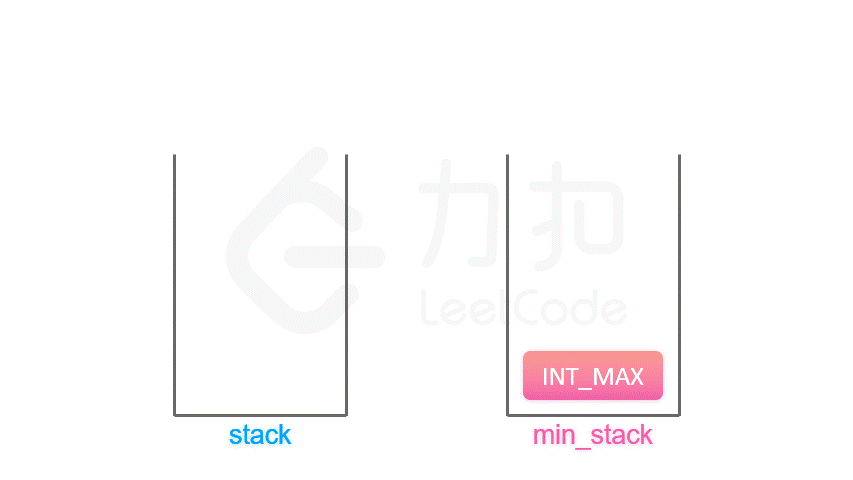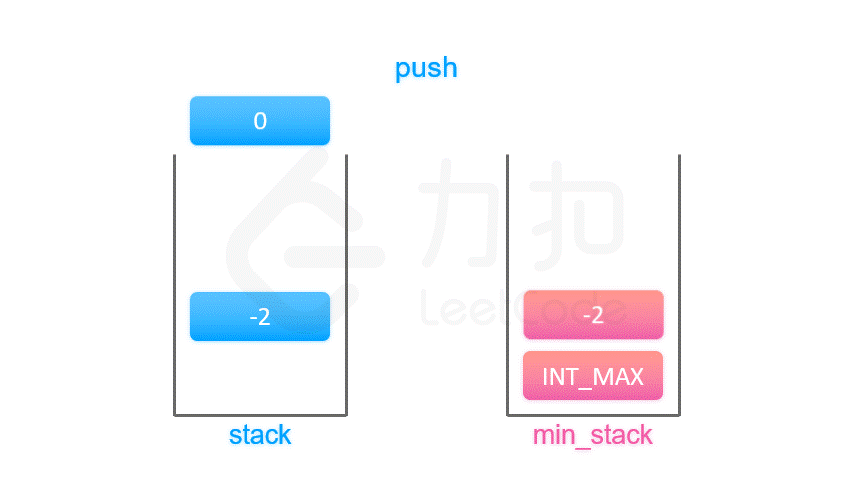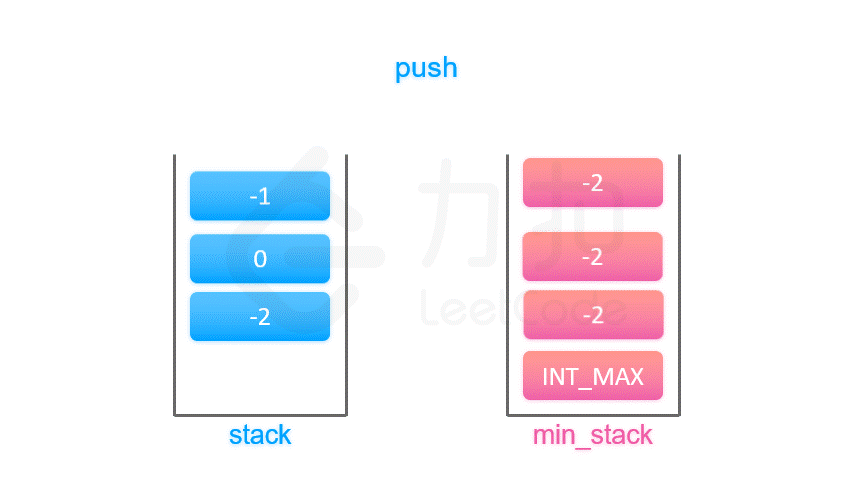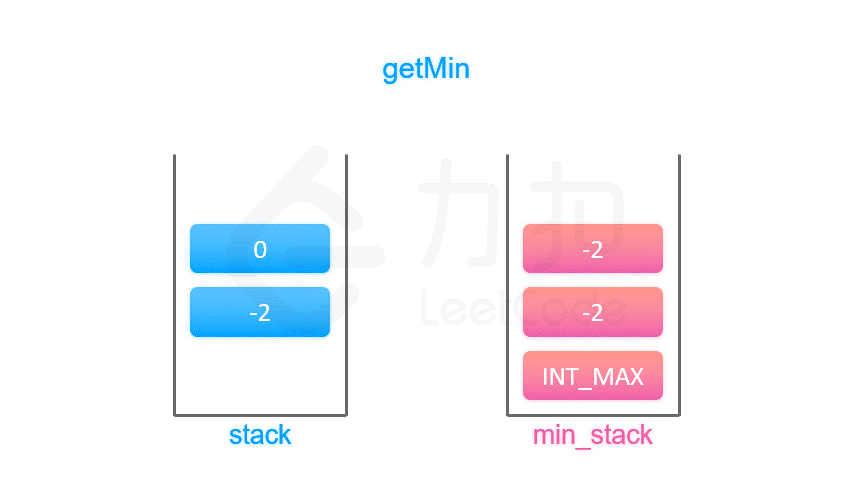
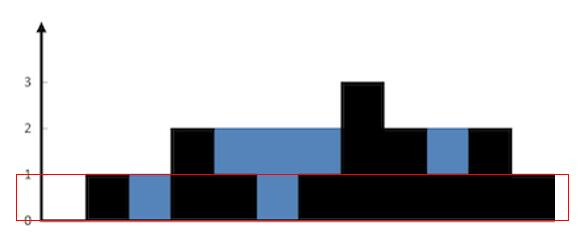
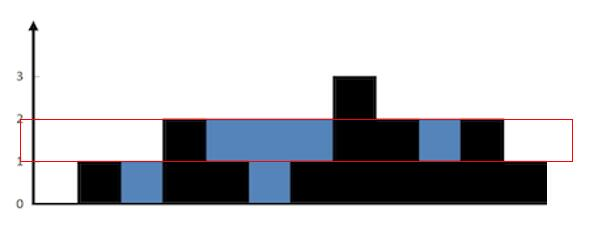
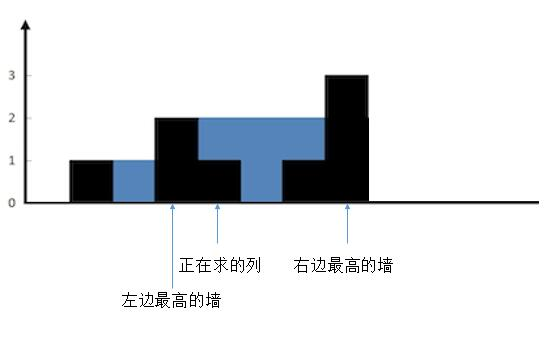


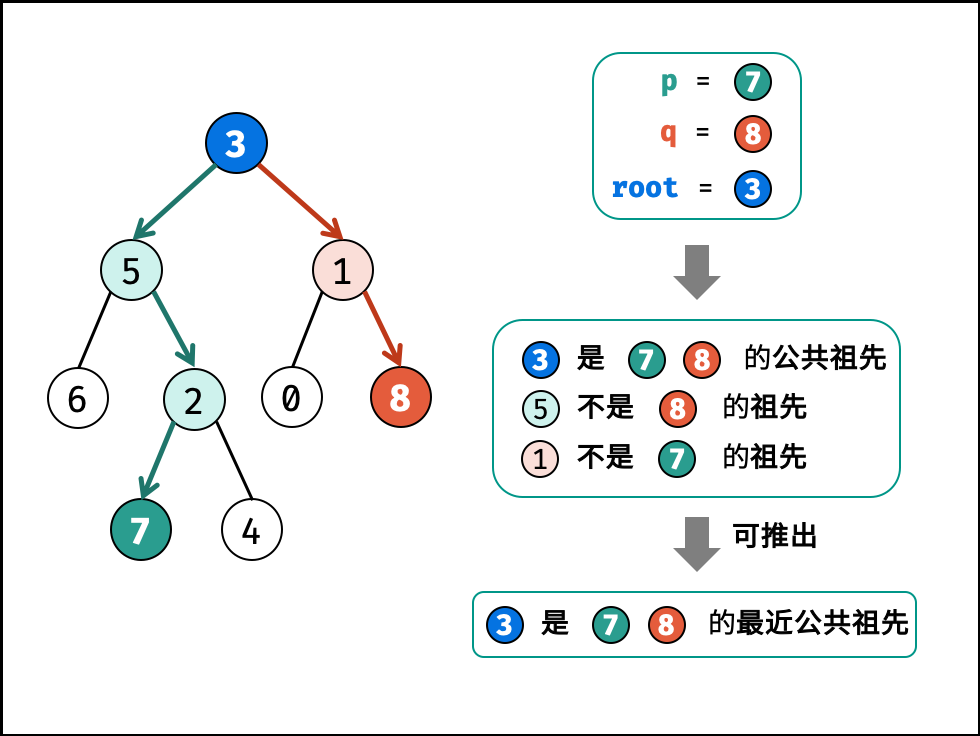
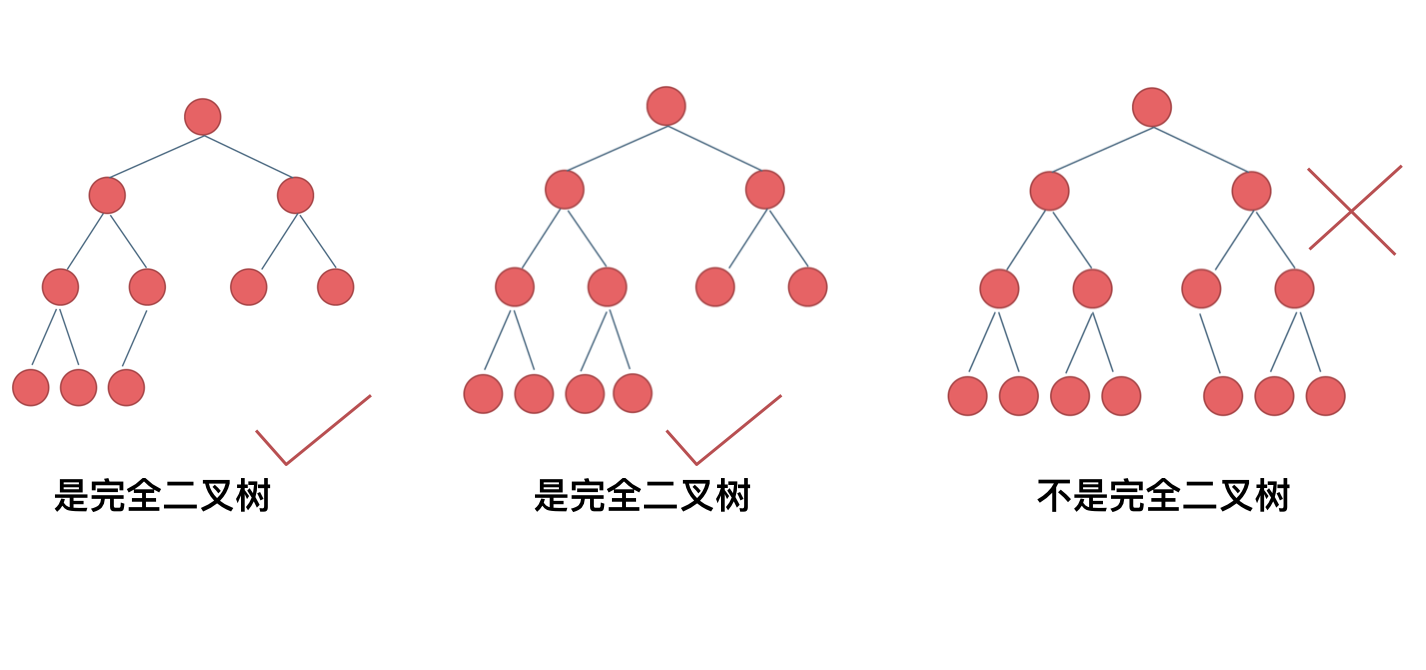
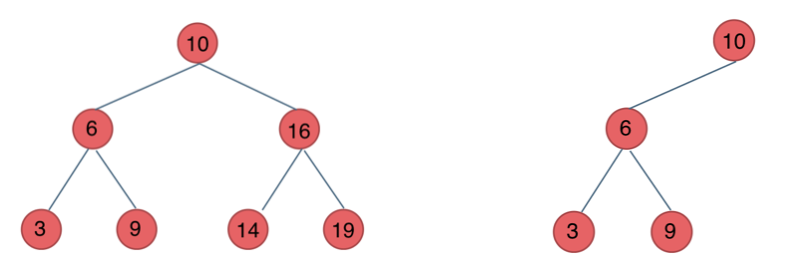
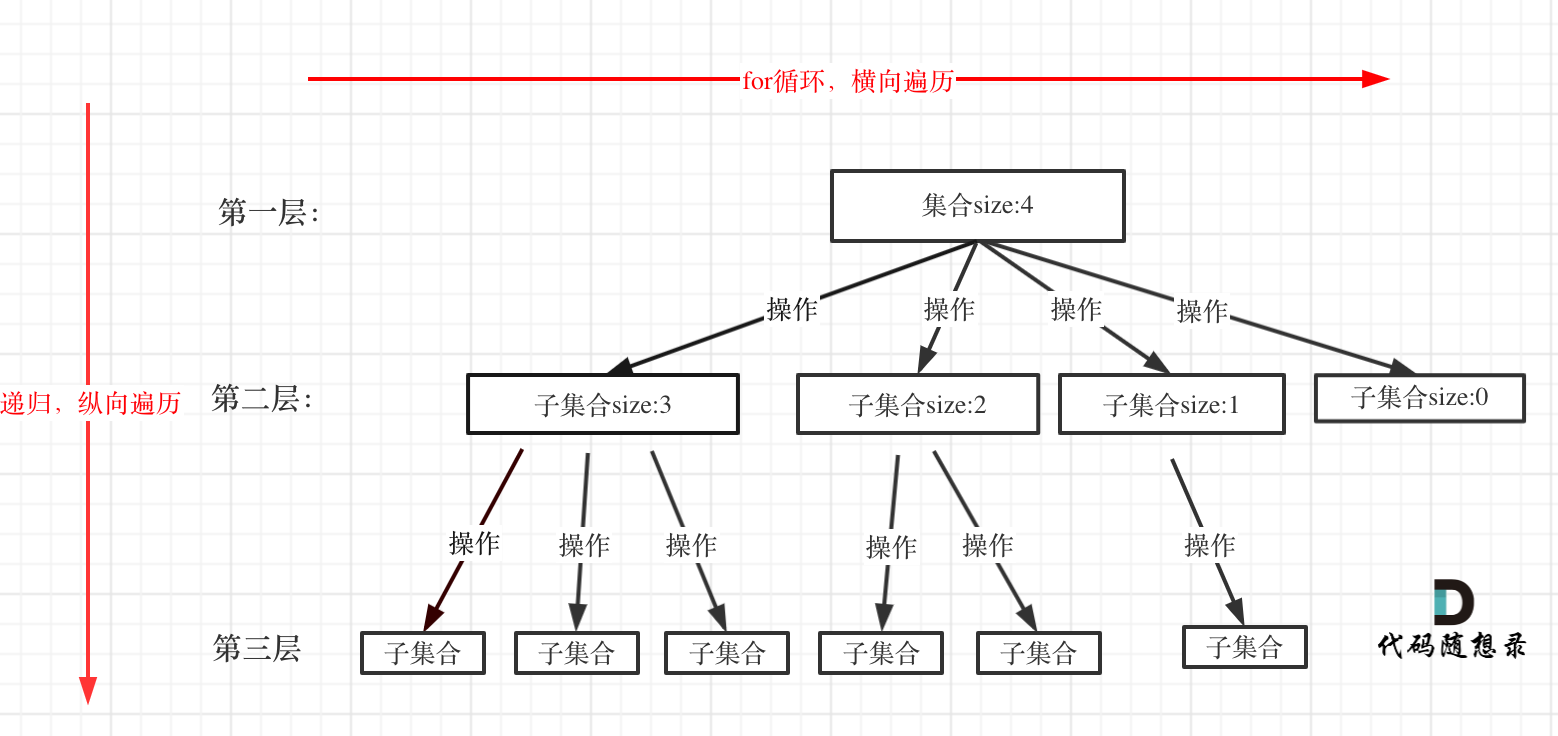
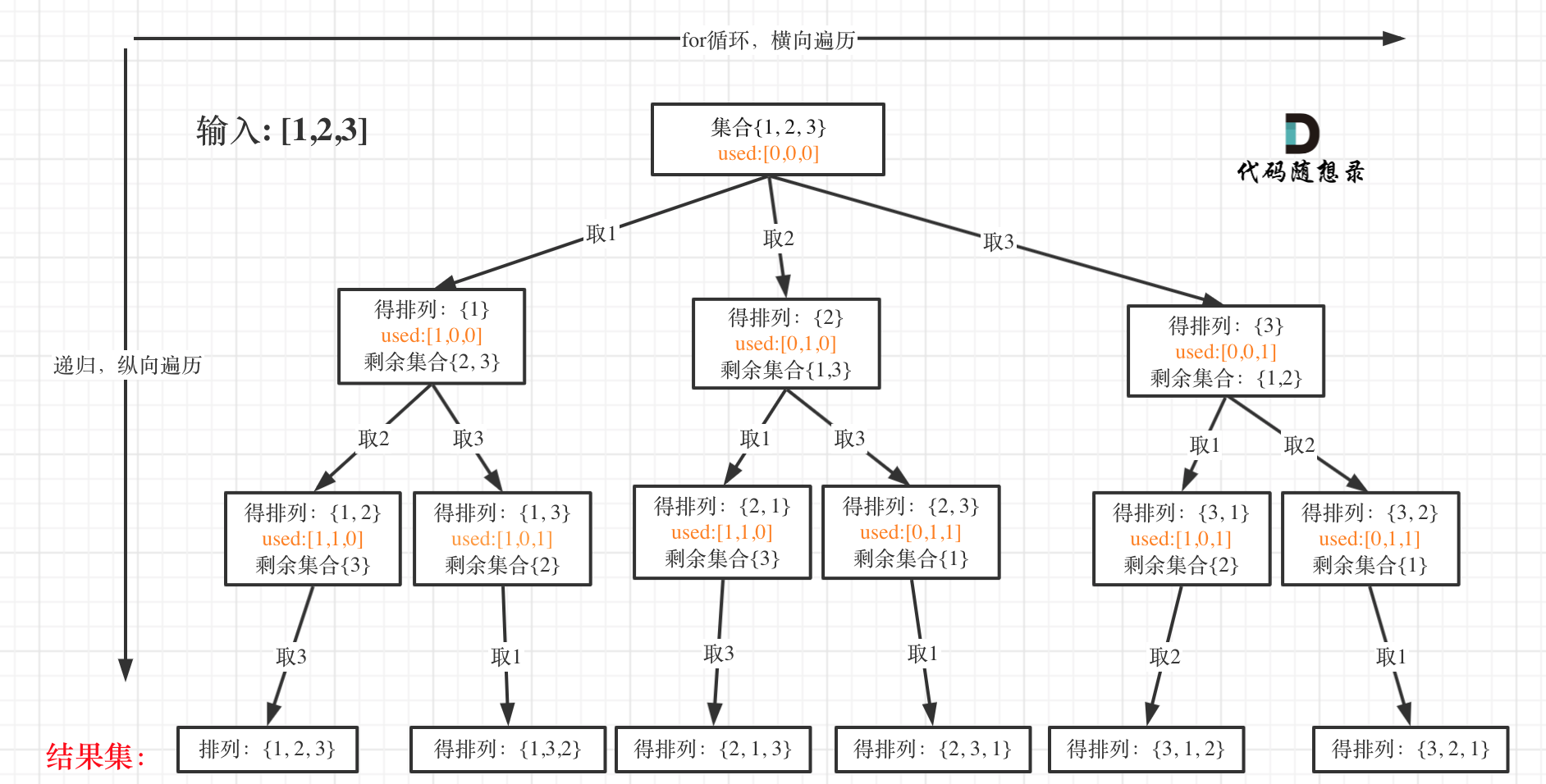
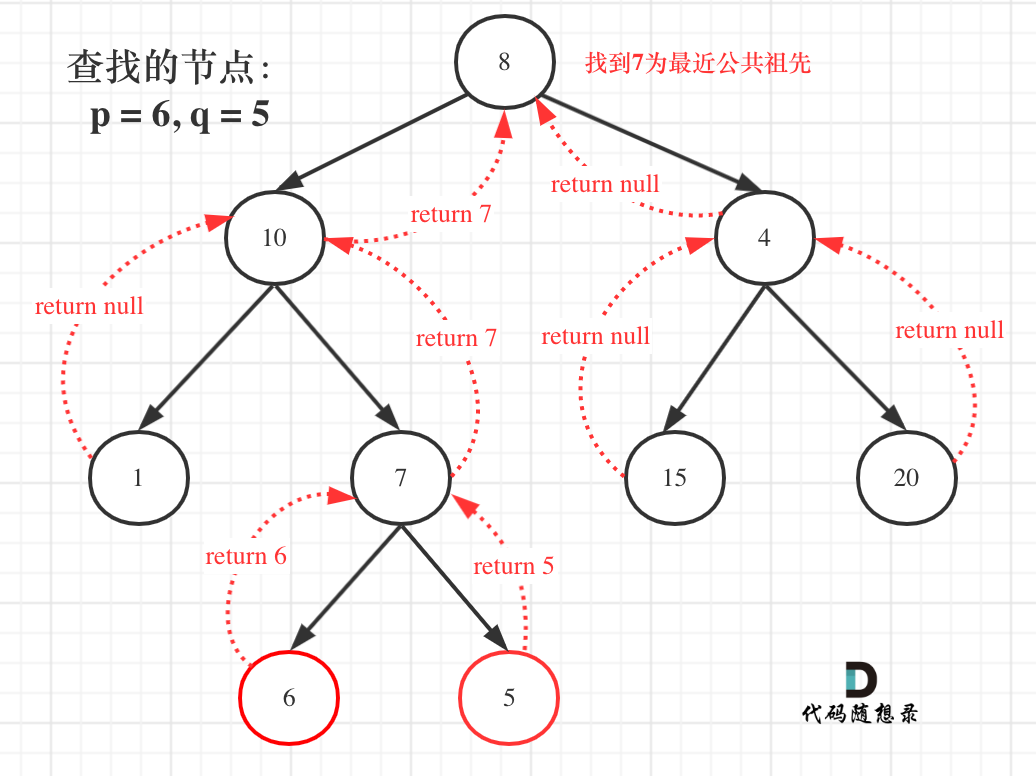
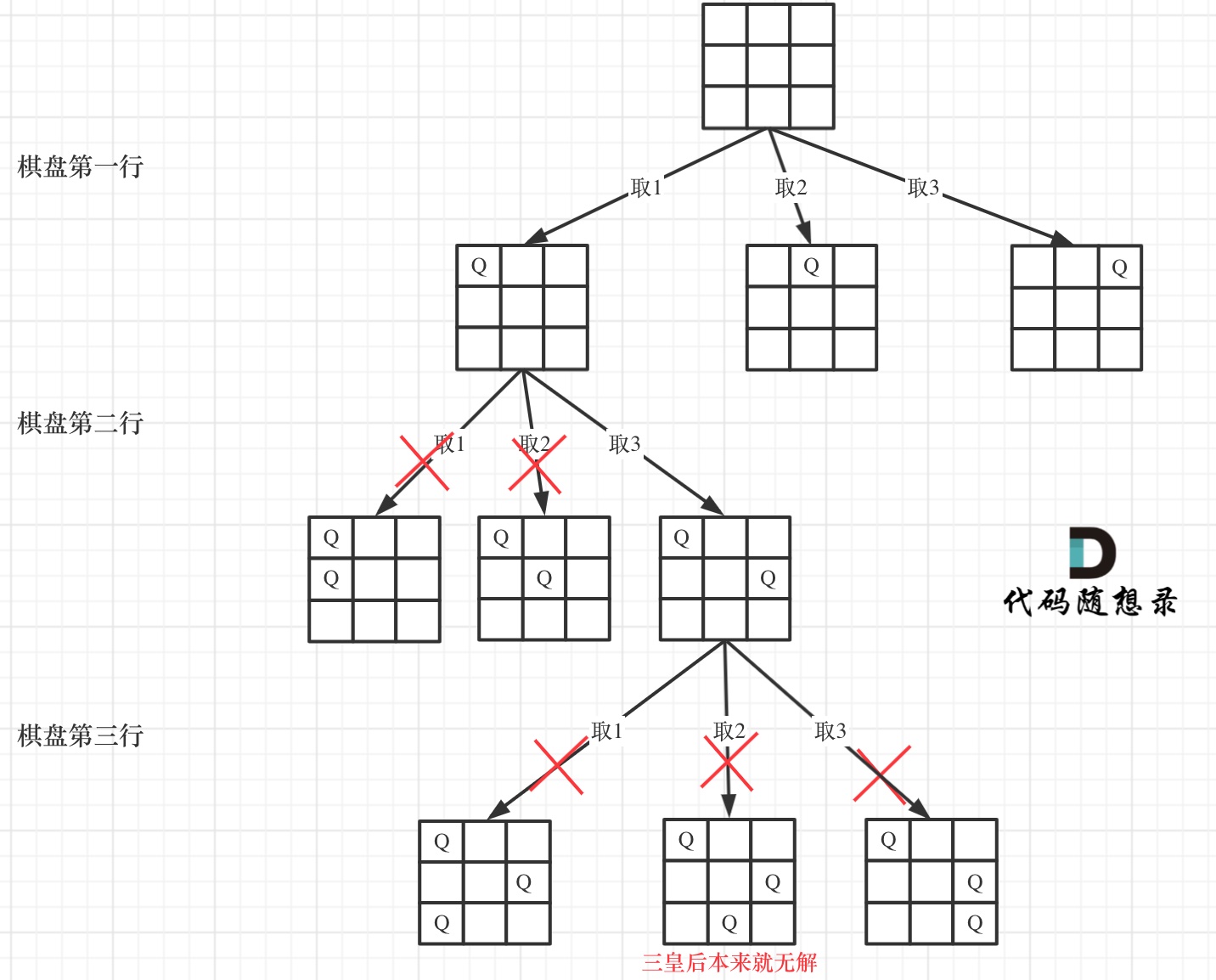
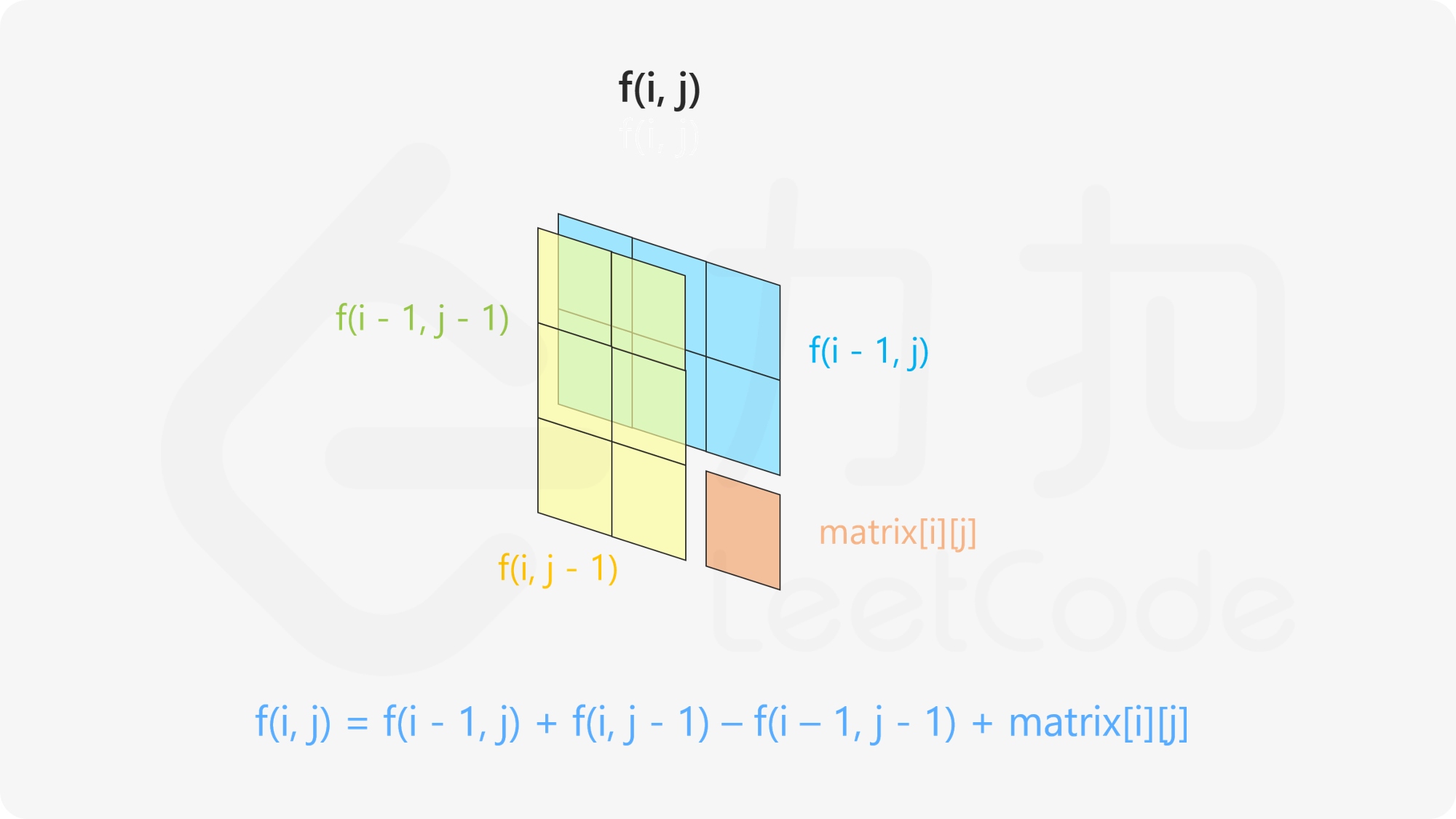

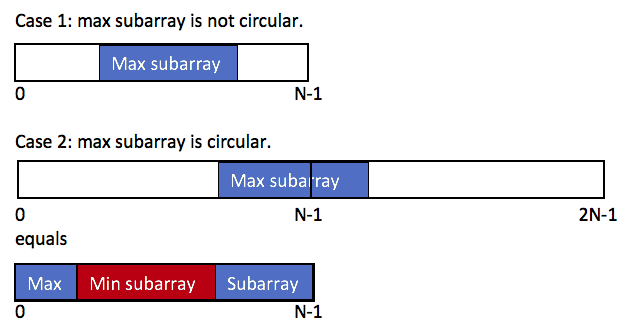
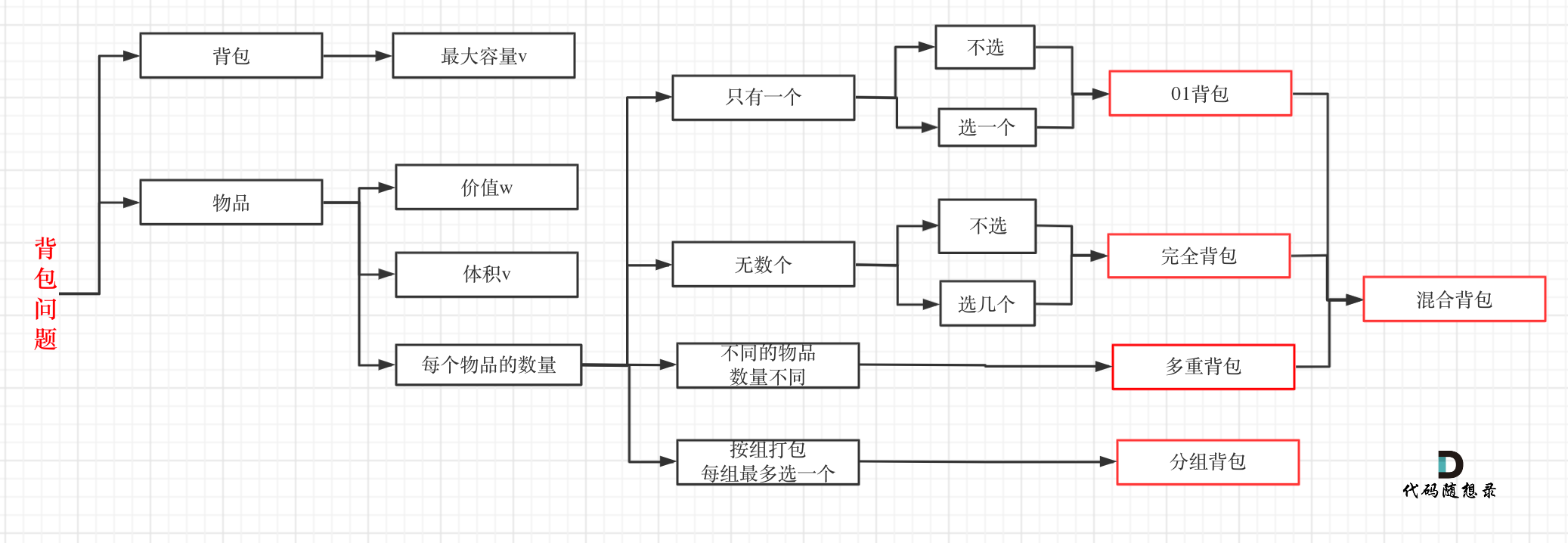
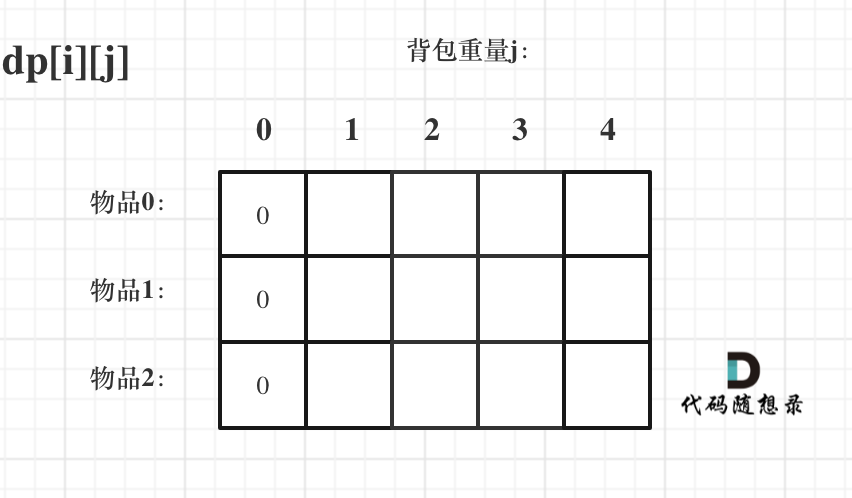
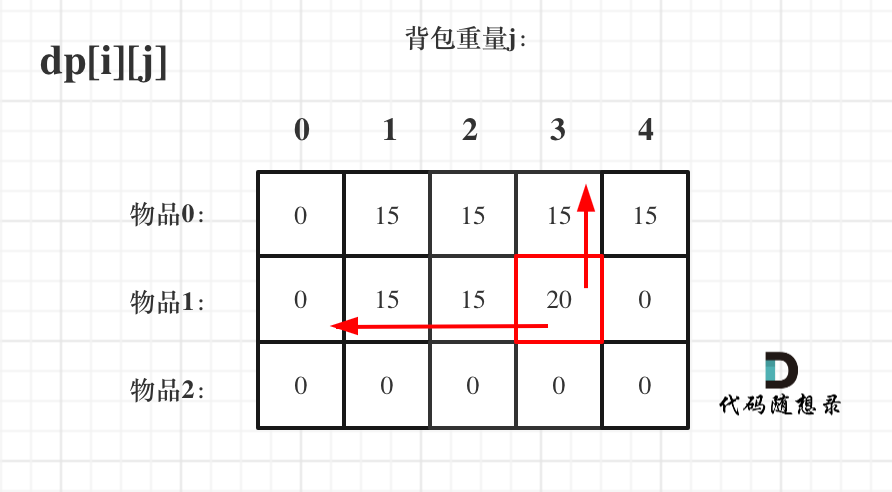
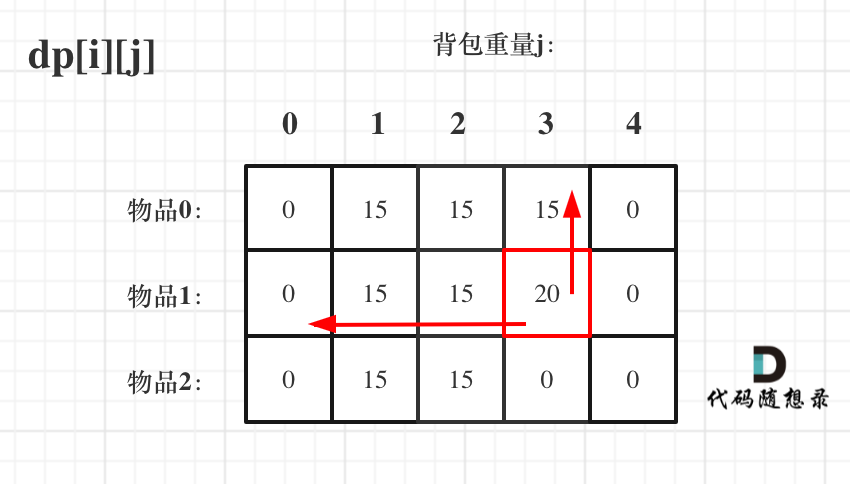

.png)
.png)